Rader's FFT algorithm
Encyclopedia
Rader's algorithm is a fast Fourier transform
(FFT) algorithm that computes the discrete Fourier transform
(DFT) of prime
sizes by re-expressing the DFT as a cyclic convolution
. (The other algorithm for FFTs of prime sizes, Bluestein's algorithm
, also works by rewriting the DFT as a convolution.)
Since Rader's algorithm only depends upon the periodicity of the DFT kernel, it is directly applicable to any other transform (of prime order) with a similar property, such as a number-theoretic transform or the discrete Hartley transform
.
The algorithm can be modified to gain a factor of two savings for the case of DFTs of real data, using a slightly modified re-indexing/permutation to obtain two half-size cyclic convolutions of real data (Chu & Burrus, 1982); an alternative adaptation for DFTs of real data, using the discrete Hartley transform, was described by Johnson & Frigo (2007).
Winograd extended Rader's algorithm to include prime-power DFT sizes
(Winograd 1976; Winograd 1978), and today Rader's algorithm is sometimes described as a special case of Winograd's FFT algorithm, also called the multiplicative Fourier transform algorithm (Tolimieri et al., 1997), which applies to an even larger class of sizes. However, for composite
sizes such as prime powers, the Cooley–Tukey FFT algorithm is much simpler and more practical to implement, so Rader's algorithm is typically only used for large-prime base cases of Cooley–Tukey's recursive
decomposition of the DFT (Frigo and Johnson, 2005).
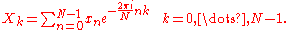
If N is a prime number, then the set of non-zero indices n = 1,...,N–1 forms a group
under multiplication modulo
N. One consequence of the number theory
of such groups is that there exists a generator
of the group (sometimes called a primitive root
), an integer g such that n = gq (mod N) for any non-zero index n and for a unique q in 0,...,N–2 (forming a bijection
from q to non-zero n). Similarly k = g–p (mod N) for any non-zero index k and for a unique p in 0,...,N–2, where the negative exponent denotes the multiplicative inverse of gp modulo N. That means that we can rewrite the DFT using these new indices p and q as:
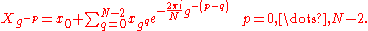
(Recall that xn and Xk are implicitly periodic in N, and also that e2πi=1. Thus, all indices and exponents are taken modulo N as required by the group arithmetic.)
The final summation, above, is precisely a cyclic convolution of the two sequences aq and bq of length N–1 (q = 0,...,N–2) defined by:
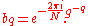
and more conventional FFT algorithms. However, that may not be efficient if N–1 itself has large prime factors, requiring recursive use of Rader's algorithm. Instead, one can compute a length-(N–1) cyclic convolution exactly by zero-padding it to a length of at least 2(N–1)–1, say to a power of two
, which can then be evaluated in O(N log N) time without the recursive application of Rader's algorithm.
This algorithm, then, requires O(N) additions plus O(N log N) time for the convolution. In practice, the O(N) additions can often be performed by absorbing the additions into the convolution: if the convolution is performed by a pair of FFTs, then the sum of xn is given by the DC (0th) output of the FFT of aq plus x0, and x0 can be added to all the outputs by adding it to the DC term of the convolution prior to the inverse FFT. Still, this algorithm requires intrinsically more operations than FFTs of nearby composite sizes, and typically takes 3–10 times as long in practice.
If Rader's algorithm is performed by using FFTs of size N–1 to compute the convolution, rather than by zero padding as mentioned above, the efficiency depends strongly upon N and the number of times that Rader's algorithm must be applied recursively. The worst case would be if N–1 were 2N2 where N2 is prime, with N2–1 = 2N3 where N3 is prime, and so on. In such cases, supposing that the chain of primes extended all the way down to some bounded value, the recursive application of Rader's algorithm would actually require O(N2) time. Such Nj are called Sophie Germain prime
s, and such a sequence of them is called a Cunningham chain
of the first kind. The lengths of Cunningham chains, however, are observed to grow more slowly than log2(N), so Rader's algorithm applied in this way is probably not Ω
(N2), though it is possibly worse than O(N log N) for the worst cases. Fortunately, a guarantee of O(N log N) complexity can be achieved by zero padding.
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) algorithm that computes the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT) of prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
sizes by re-expressing the DFT as a cyclic convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
. (The other algorithm for FFTs of prime sizes, Bluestein's algorithm
Bluestein's FFT algorithm
Bluestein's FFT algorithm , commonly called the chirp z-transform algorithm , is a fast Fourier transform algorithm that computes the discrete Fourier transform of arbitrary sizes by re-expressing the DFT as a convolution...
, also works by rewriting the DFT as a convolution.)
Since Rader's algorithm only depends upon the periodicity of the DFT kernel, it is directly applicable to any other transform (of prime order) with a similar property, such as a number-theoretic transform or the discrete Hartley transform
Discrete Hartley transform
A discrete Hartley transform is a Fourier-related transform of discrete, periodic data similar to the discrete Fourier transform , with analogous applications in signal processing and related fields. Its main distinction from the DFT is that it transforms real inputs to real outputs, with no...
.
The algorithm can be modified to gain a factor of two savings for the case of DFTs of real data, using a slightly modified re-indexing/permutation to obtain two half-size cyclic convolutions of real data (Chu & Burrus, 1982); an alternative adaptation for DFTs of real data, using the discrete Hartley transform, was described by Johnson & Frigo (2007).
Winograd extended Rader's algorithm to include prime-power DFT sizes
(Winograd 1976; Winograd 1978), and today Rader's algorithm is sometimes described as a special case of Winograd's FFT algorithm, also called the multiplicative Fourier transform algorithm (Tolimieri et al., 1997), which applies to an even larger class of sizes. However, for compositeComposite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
sizes such as prime powers, the Cooley–Tukey FFT algorithm is much simpler and more practical to implement, so Rader's algorithm is typically only used for large-prime base cases of Cooley–Tukey's recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
decomposition of the DFT (Frigo and Johnson, 2005).
Algorithm
Recall that the DFT is defined by the formula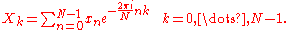If N is a prime number, then the set of non-zero indices n = 1,...,N–1 forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under multiplication modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
N. One consequence of the number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
of such groups is that there exists a generator
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of the group (sometimes called a primitive root
Primitive root modulo n
In modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
), an integer g such that n = gq (mod N) for any non-zero index n and for a unique q in 0,...,N–2 (forming a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
from q to non-zero n). Similarly k = g–p (mod N) for any non-zero index k and for a unique p in 0,...,N–2, where the negative exponent denotes the multiplicative inverse of gp modulo N. That means that we can rewrite the DFT using these new indices p and q as:
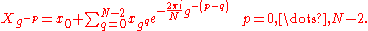
(Recall that xn and Xk are implicitly periodic in N, and also that e2πi=1. Thus, all indices and exponents are taken modulo N as required by the group arithmetic.)
The final summation, above, is precisely a cyclic convolution of the two sequences aq and bq of length N–1 (q = 0,...,N–2) defined by:
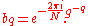
Evaluating the convolution
Since N–1 is composite, this convolution can be performed directly via the convolution theoremConvolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
and more conventional FFT algorithms. However, that may not be efficient if N–1 itself has large prime factors, requiring recursive use of Rader's algorithm. Instead, one can compute a length-(N–1) cyclic convolution exactly by zero-padding it to a length of at least 2(N–1)–1, say to a power of two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
, which can then be evaluated in O(N log N) time without the recursive application of Rader's algorithm.
This algorithm, then, requires O(N) additions plus O(N log N) time for the convolution. In practice, the O(N) additions can often be performed by absorbing the additions into the convolution: if the convolution is performed by a pair of FFTs, then the sum of xn is given by the DC (0th) output of the FFT of aq plus x0, and x0 can be added to all the outputs by adding it to the DC term of the convolution prior to the inverse FFT. Still, this algorithm requires intrinsically more operations than FFTs of nearby composite sizes, and typically takes 3–10 times as long in practice.
If Rader's algorithm is performed by using FFTs of size N–1 to compute the convolution, rather than by zero padding as mentioned above, the efficiency depends strongly upon N and the number of times that Rader's algorithm must be applied recursively. The worst case would be if N–1 were 2N2 where N2 is prime, with N2–1 = 2N3 where N3 is prime, and so on. In such cases, supposing that the chain of primes extended all the way down to some bounded value, the recursive application of Rader's algorithm would actually require O(N2) time. Such Nj are called Sophie Germain prime
Sophie Germain prime
In number theory, a prime number p is a Sophie Germain prime if 2p + 1 is also prime. For example, 23 is a Sophie Germain prime because it is a prime and 2 × 23 + 1 = 47, and 47 is also a prime number...
s, and such a sequence of them is called a Cunningham chain
Cunningham chain
In mathematics, a Cunningham chain is a certain sequence of prime numbers. Cunningham chains are named after mathematician A. J. C. Cunningham. They are also called chains of nearly doubled primes....
of the first kind. The lengths of Cunningham chains, however, are observed to grow more slowly than log2(N), so Rader's algorithm applied in this way is probably not Ω
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(N2), though it is possibly worse than O(N log N) for the worst cases. Fortunately, a guarantee of O(N log N) complexity can be achieved by zero padding.