Discrete Hartley transform
Encyclopedia
A discrete Hartley transform (DHT) is a Fourier-related transform of discrete, periodic data similar to the discrete Fourier transform
(DFT), with analogous applications in signal processing and related fields. Its main distinction from the DFT is that it transforms real inputs to real outputs, with no intrinsic involvement of complex number
s. Just as the DFT is the discrete analogue of the continuous Fourier transform
, the DHT is the discrete analogue of the continuous Hartley transform
, introduced by R. V. L. Hartley
in 1942.
Because there are fast algorithms for the DHT analogous to the fast Fourier transform
(FFT), the DHT was originally proposed by R. N. Bracewell
in 1983 as a more efficient computational tool in the common case where the data are purely real. It was subsequently argued, however, that specialized FFT algorithms for real inputs or outputs can ordinarily be found with slightly fewer operations than any corresponding algorithm for the DHT (see below).
H : Rn -> Rn (where R denotes the set of real number
s). The N real numbers x0, ...., xN-1 are transformed into the N real numbers H0, ..., HN-1 according to the formula
.
The combination
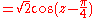is sometimes denoted 
, and should be contrasted with the 
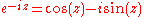that appears in the DFT definition (where i is the imaginary unit
).
As with the DFT, the overall scale factor in front of the transform and the sign of the sine term are a matter of convention. Although these conventions occasionally vary between authors, they do not affect the essential properties of the transform.
The DHT can be used to compute the DFT, and vice versa. For real inputs xn, the DFT output Xk has a real part (Hk + HN-k)/2 and an imaginary part (HN-k - Hk)/2. Conversely, the DHT is equivalent to computing the DFT of xn multiplied by 1+i, then taking the real part of the result.
As with the DFT, a cyclic convolution
z = x*y of two vectors x = (xn) and y = (yn) to produce a vector z = (zn), all of length N, becomes a simple operation after the DHT. In particular, suppose that the vectors X, Y, and Z denote the DHT of x, y, and z respectively. Then the elements of Z are given by:
where we take all of the vectors to be periodic in N (XN = X0, etcetera). Thus, just as the DFT transforms a convolution into a pointwise multiplication of complex numbers (pairs of real and imaginary parts), the DHT transforms a convolution into a simple combination of pairs of real frequency components. The inverse DHT then yields the desired vector z. In this way, a fast algorithm for the DHT (see below) yields a fast algorithm for convolution. (Note that this is slightly more expensive than the corresponding procedure for the DFT, not including the costs of the transforms below, because the pairwise operation above requires 8 real-arithmetic operations compared to the 6 of a complex multiplication. This count doesn't include the division by 2, which can be absorbed e.g. into the 1/N normalization of the inverse DHT.)
). There are fast algorithms similar to the FFT, however, that compute the same result in only O(N log N) operations. Nearly every FFT algorithm, from Cooley-Tukey
to Prime-Factor
to Winograd (Sorensen et al., 1985) to Bruun's
(Bini & Bozzo, 1993), has a direct analogue for the discrete Hartley transform. (However, a few of the more exotic FFT algorithms, such as the QFT, have not yet been investigated in the context of the DHT.)
In particular, the DHT analogue of the Cooley-Tukey algorithm is commonly known as the Fast Hartley Transform (FHT) algorithm, and was first described by Bracewell in 1984. This FHT algorithm, at least when applied to power-of-two
sizes N, is the subject of the United States patent
number 4,646,256, issued in 1987 to Stanford University
. Stanford placed this patent in the public domain in 1994 (Bracewell, 1995).
As mentioned above, DHT algorithms are typically slightly less efficient (in terms of the number of floating-point operations) than the corresponding DFT algorithm (FFT) specialized for real inputs (or outputs). This was first argued by Sorensen et al. (1987) and Duhamel & Vetterli (1987). The latter authors obtained what appears to be the lowest published operation count for the DHT of power-of-two sizes, employing a split-radix algorithm (similar to the split-radix FFT
) that breaks a DHT of length N into a DHT of length N/2 and two real-input DFTs (not DHTs) of length N/4. In this way, they argued that a DHT of power-of-two length can be computed with, at best, 2 more additions than the corresponding number of arithmetic operations for the real-input DFT.
On present-day computers, performance is determined more by cache
and CPU pipeline considerations than by strict operation counts, and a slight difference in arithmetic cost is unlikely to be significant. Since FHT and real-input FFT algorithms have similar computational structures, neither appears to have a substantial a priori speed advantage (Popovic and Sevic, 1994). As a practical matter, highly optimized real-input FFT libraries are available from many sources (e.g. from CPU vendors such as Intel), whereas highly optimized DHT libraries are less common.
On the other hand, the redundant computations in FFTs due to real inputs are more difficult to eliminate for large prime
N, despite the existence of O(N log N) complex-data algorithms for such cases, because the redundancies are hidden behind intricate permutations and/or phase rotations in those algorithms. In contrast, a standard prime-size FFT algorithm, Rader's algorithm
, can be directly applied to the DHT of real data for roughly a factor of two less computation than that of the equivalent complex FFT (Frigo and Johnson, 2005). On the other hand, a non-DHT-based adaptation of Rader's algorithm for real-input DFTs is also possible (Chu & Burrus
, 1982).
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT), with analogous applications in signal processing and related fields. Its main distinction from the DFT is that it transforms real inputs to real outputs, with no intrinsic involvement of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. Just as the DFT is the discrete analogue of the continuous Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, the DHT is the discrete analogue of the continuous Hartley transform
Hartley transform
In mathematics, the Hartley transform is an integral transform closely related to the Fourier transform, but which transforms real-valued functions to real-valued functions. It was proposed as an alternative to the Fourier transform by R. V. L. Hartley in 1942, and is one of many known...
, introduced by R. V. L. Hartley
Ralph Hartley
Ralph Vinton Lyon Hartley was an electronics researcher. He invented the Hartley oscillator and the Hartley transform, and contributed to the foundations of information theory.-Biography:...
in 1942.
Because there are fast algorithms for the DHT analogous to the fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT), the DHT was originally proposed by R. N. Bracewell
Ronald N. Bracewell
Ronald Newbold Bracewell AO was the Lewis M. Terman Professor of Electrical Engineering, Emeritus of the at Stanford University.- Education :...
in 1983 as a more efficient computational tool in the common case where the data are purely real. It was subsequently argued, however, that specialized FFT algorithms for real inputs or outputs can ordinarily be found with slightly fewer operations than any corresponding algorithm for the DHT (see below).
Definition
Formally, the discrete Hartley transform is a linear, invertible functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
H : Rn -> Rn (where R denotes the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s). The N real numbers x0, ...., xN-1 are transformed into the N real numbers H0, ..., HN-1 according to the formula
.The combination
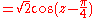is sometimes denoted , and should be contrasted with the 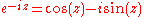that appears in the DFT definition (where i is the imaginary unitImaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
).
As with the DFT, the overall scale factor in front of the transform and the sign of the sine term are a matter of convention. Although these conventions occasionally vary between authors, they do not affect the essential properties of the transform.
Properties
The transform can be interpreted as the multiplication of the vector (x0, ...., xN-1) by an N-by-N matrix; therefore, the discrete Hartley transform is a linear operator. The matrix is invertible; the inverse transformation, which allows one to recover the xn from the Hk, is simply the DHT of Hk multiplied by 1/N. That is, the DHT is its own inverse (involutary), up to an overall scale factor.The DHT can be used to compute the DFT, and vice versa. For real inputs xn, the DFT output Xk has a real part (Hk + HN-k)/2 and an imaginary part (HN-k - Hk)/2. Conversely, the DHT is equivalent to computing the DFT of xn multiplied by 1+i, then taking the real part of the result.
As with the DFT, a cyclic convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
z = x*y of two vectors x = (xn) and y = (yn) to produce a vector z = (zn), all of length N, becomes a simple operation after the DHT. In particular, suppose that the vectors X, Y, and Z denote the DHT of x, y, and z respectively. Then the elements of Z are given by:
where we take all of the vectors to be periodic in N (XN = X0, etcetera). Thus, just as the DFT transforms a convolution into a pointwise multiplication of complex numbers (pairs of real and imaginary parts), the DHT transforms a convolution into a simple combination of pairs of real frequency components. The inverse DHT then yields the desired vector z. In this way, a fast algorithm for the DHT (see below) yields a fast algorithm for convolution. (Note that this is slightly more expensive than the corresponding procedure for the DFT, not including the costs of the transforms below, because the pairwise operation above requires 8 real-arithmetic operations compared to the 6 of a complex multiplication. This count doesn't include the division by 2, which can be absorbed e.g. into the 1/N normalization of the inverse DHT.)
Fast algorithms
Just as for the DFT, evaluating the DHT definition directly would require O(N2) arithmetical operations (see Big O notationBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
). There are fast algorithms similar to the FFT, however, that compute the same result in only O(N log N) operations. Nearly every FFT algorithm, from Cooley-Tukey
Cooley-Tukey FFT algorithm
The Cooley–Tukey algorithm, named after J.W. Cooley and John Tukey, is the most common fast Fourier transform algorithm. It re-expresses the discrete Fourier transform of an arbitrary composite size N = N1N2 in terms of smaller DFTs of sizes N1 and N2, recursively, in order to reduce the...
to Prime-Factor
Prime-factor FFT algorithm
The prime-factor algorithm , also called the Good–Thomas algorithm , is a fast Fourier transform algorithm that re-expresses the discrete Fourier transform of a size N = N1N2 as a two-dimensional N1×N2 DFT, but only for the case where N1 and N2 are relatively prime...
to Winograd (Sorensen et al., 1985) to Bruun's
Bruun's FFT algorithm
Bruun's algorithm is a fast Fourier transform algorithm based on an unusual recursive polynomial-factorization approach, proposed for powers of two by G. Bruun in 1978 and generalized to arbitrary even composite sizes by H. Murakami in 1996...
(Bini & Bozzo, 1993), has a direct analogue for the discrete Hartley transform. (However, a few of the more exotic FFT algorithms, such as the QFT, have not yet been investigated in the context of the DHT.)
In particular, the DHT analogue of the Cooley-Tukey algorithm is commonly known as the Fast Hartley Transform (FHT) algorithm, and was first described by Bracewell in 1984. This FHT algorithm, at least when applied to power-of-two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
sizes N, is the subject of the United States patent
Software patent
Software patent does not have a universally accepted definition. One definition suggested by the Foundation for a Free Information Infrastructure is that a software patent is a "patent on any performance of a computer realised by means of a computer program".In 2005, the European Patent Office...
number 4,646,256, issued in 1987 to Stanford University
Stanford University
The Leland Stanford Junior University, commonly referred to as Stanford University or Stanford, is a private research university on an campus located near Palo Alto, California. It is situated in the northwestern Santa Clara Valley on the San Francisco Peninsula, approximately northwest of San...
. Stanford placed this patent in the public domain in 1994 (Bracewell, 1995).
As mentioned above, DHT algorithms are typically slightly less efficient (in terms of the number of floating-point operations) than the corresponding DFT algorithm (FFT) specialized for real inputs (or outputs). This was first argued by Sorensen et al. (1987) and Duhamel & Vetterli (1987). The latter authors obtained what appears to be the lowest published operation count for the DHT of power-of-two sizes, employing a split-radix algorithm (similar to the split-radix FFT
Split-radix FFT algorithm
The split-radix FFT is a fast Fourier transform algorithm for computing the discrete Fourier transform , and was first described in an initially little-appreciated paper by R. Yavne and subsequently rediscovered simultaneously by various authors in 1984. The split-radix FFT is a fast Fourier...
) that breaks a DHT of length N into a DHT of length N/2 and two real-input DFTs (not DHTs) of length N/4. In this way, they argued that a DHT of power-of-two length can be computed with, at best, 2 more additions than the corresponding number of arithmetic operations for the real-input DFT.
On present-day computers, performance is determined more by cache
CPU cache
A CPU cache is a cache used by the central processing unit of a computer to reduce the average time to access memory. The cache is a smaller, faster memory which stores copies of the data from the most frequently used main memory locations...
and CPU pipeline considerations than by strict operation counts, and a slight difference in arithmetic cost is unlikely to be significant. Since FHT and real-input FFT algorithms have similar computational structures, neither appears to have a substantial a priori speed advantage (Popovic and Sevic, 1994). As a practical matter, highly optimized real-input FFT libraries are available from many sources (e.g. from CPU vendors such as Intel), whereas highly optimized DHT libraries are less common.
On the other hand, the redundant computations in FFTs due to real inputs are more difficult to eliminate for large prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
N, despite the existence of O(N log N) complex-data algorithms for such cases, because the redundancies are hidden behind intricate permutations and/or phase rotations in those algorithms. In contrast, a standard prime-size FFT algorithm, Rader's algorithm
Rader's FFT algorithm
Rader's algorithm is a fast Fourier transform algorithm that computes the discrete Fourier transform of prime sizes by re-expressing the DFT as a cyclic convolution...
, can be directly applied to the DHT of real data for roughly a factor of two less computation than that of the equivalent complex FFT (Frigo and Johnson, 2005). On the other hand, a non-DHT-based adaptation of Rader's algorithm for real-input DFTs is also possible (Chu & Burrus
C. Sidney Burrus
Charles Sidney Burrus is an American electrical engineer and the Maxfield and Oshman Professor Emeritus of Electrical and Computer Engineering at Rice University in Houston, Texas...
, 1982).