
Cunningham chain
Encyclopedia
In mathematics
, a Cunningham chain is a certain sequence of prime number
s. Cunningham chains are named after mathematician
A. J. C. Cunningham
. They are also called chains of nearly doubled primes.
A Cunningham chain of the first kind of length n is a sequence of prime numbers (p1,...,pn) such that for all 1 ≤ i < n, pi+1 = 2 pi + 1. (Hence each term of such a chain except the last one is a Sophie Germain prime
, and each term except the first is a safe prime
).
It follows that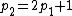 ,
, 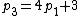 ,
, 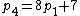 , ...,
, ..., 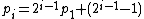 .
.
Similarly, a Cunningham chain of the second kind of length n is a sequence of prime numbers (p1,...,pn) such that for all 1 ≤ i < n, pi+1 = 2 pi - 1.
Cunningham chains are also sometimes generalized to sequences of prime numbers (p1,...,pn) such that for all 1 ≤ i < n, pi+1 = api + b for fixed coprime
integer
s a, b; the resulting chains are called generalized Cunningham chains.
A Cunningham chain is called complete if it cannot be further extended, i.e., if the previous or next term in the chain would not be a prime number anymore.
Cunningham chains are now considered useful in cryptographic systems since "they provide two concurrent suitable settings for the ElGamal cryptosystem ... [which] can be implemented in any field where the discrete logarithm problem is difficult."
and the broader Schinzel's hypothesis H
, both widely believed to be true, that for every k there are infinitely many Cunningham chains of length k. There are, however, no known direct methods of generating such chains.
q# denotes the primorial
2×3×5×7×...×q.
, the longest known Cunningham chain of either kind is of length 17. The first known was of the 1st kind starting at 2759832934171386593519, discovered by Jaroslaw Wroblewski in 2008 where he also found some of the 2nd kind.
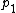 be the first prime of a Cunningham chain of the first kind. The first prime is odd, thus
be the first prime of a Cunningham chain of the first kind. The first prime is odd, thus 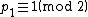 . Since each successive prime in the chain is
. Since each successive prime in the chain is 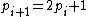 it follows that
it follows that 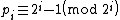 . Thus,
. Thus,  ,
, 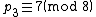 , and so forth.
, and so forth.
The above property can be informally observed by considering the primes of a chain in base 2. (Note that, as with all bases, multiplying by the number of the base "shifts" the digits to the left.) When we consider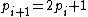 in base 2, we see that, by multiplying
in base 2, we see that, by multiplying 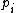 by 2, the least significant digit of
by 2, the least significant digit of 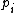 becomes the secondmost least significant digit of
becomes the secondmost least significant digit of  . Because
. Because 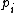 is odd--that is, the least significant digit is 1 in base 2--we know that the secondmost least significant digit of
is odd--that is, the least significant digit is 1 in base 2--we know that the secondmost least significant digit of 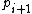 is also 1. And, finally, we can see that
is also 1. And, finally, we can see that 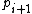 will be odd due to the addition of 1 to
will be odd due to the addition of 1 to 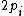 . In this way, successive primes in a Cunningham chain are essentially shifted left in binary with ones filling in the least significant digits. For example, here is a complete length 6 chain which starts at 141361469:
. In this way, successive primes in a Cunningham chain are essentially shifted left in binary with ones filling in the least significant digits. For example, here is a complete length 6 chain which starts at 141361469:
A similar result holds for Cunningham chains of the second kind. From the observation that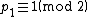 and the relation
and the relation 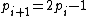 it follows that
it follows that  . In binary notation, the primes in a Cunningham chain of the second kind end with a pattern "0...01", where, for each
. In binary notation, the primes in a Cunningham chain of the second kind end with a pattern "0...01", where, for each 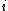 , the number of zeros in the pattern for
, the number of zeros in the pattern for 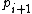 is one more than the number of zeros for
is one more than the number of zeros for  . As with Cunningham chains of the first kind, the bits left of the pattern shift left by one position with each successive prime.
. As with Cunningham chains of the first kind, the bits left of the pattern shift left by one position with each successive prime.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Cunningham chain is a certain sequence of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. Cunningham chains are named after mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
A. J. C. Cunningham
Allan Joseph Champneys Cunningham
The British mathematician Allan Joseph Champneys Cunningham started a military career with the East India Company's Bengal Engineers. During 1871–1881, he was Instructor in Mathematics at the Thomason Civil Engineering College, Roorkee...
. They are also called chains of nearly doubled primes.
A Cunningham chain of the first kind of length n is a sequence of prime numbers (p1,...,pn) such that for all 1 ≤ i < n, pi+1 = 2 pi + 1. (Hence each term of such a chain except the last one is a Sophie Germain prime
Sophie Germain prime
In number theory, a prime number p is a Sophie Germain prime if 2p + 1 is also prime. For example, 23 is a Sophie Germain prime because it is a prime and 2 × 23 + 1 = 47, and 47 is also a prime number...
, and each term except the first is a safe prime
Safe prime
A safe prime is a prime number of the form 2p + 1, where p is also a prime. The first few safe primes are...
).
It follows that
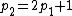 ,
, 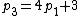 ,
, 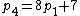 , ...,
, ..., 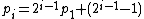 .
.Similarly, a Cunningham chain of the second kind of length n is a sequence of prime numbers (p1,...,pn) such that for all 1 ≤ i < n, pi+1 = 2 pi - 1.
Cunningham chains are also sometimes generalized to sequences of prime numbers (p1,...,pn) such that for all 1 ≤ i < n, pi+1 = api + b for fixed coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s a, b; the resulting chains are called generalized Cunningham chains.
A Cunningham chain is called complete if it cannot be further extended, i.e., if the previous or next term in the chain would not be a prime number anymore.
Cunningham chains are now considered useful in cryptographic systems since "they provide two concurrent suitable settings for the ElGamal cryptosystem ... [which] can be implemented in any field where the discrete logarithm problem is difficult."
Largest known Cunningham chains
It follows from Dickson's conjectureDickson's conjecture
In number theory, a branch of mathematics, Dickson's conjecture is the conjecture stated by that for a finite set of linear forms , , ..., with , there are infinitely many positive integers for which they are all prime, unless there is a congruence condition preventing this...
and the broader Schinzel's hypothesis H
Schinzel's hypothesis H
In mathematics, Schinzel's hypothesis H is a very broad generalisation of conjectures such as the twin prime conjecture. It aims to define the possible scope of a conjecture of the nature that several sequences of the type...
, both widely believed to be true, that for every k there are infinitely many Cunningham chains of length k. There are, however, no known direct methods of generating such chains.
| k | Kind | p1 (starting prime) | Digits | Year | Discoverer |
|---|---|---|---|---|---|
| 1 | 1st | 243112609 − 1 | 12978189 | 2008 | GIMPS / Edson Smith |
| 2 | 1st | 183027×2265440 − 1 | 79911 | 2010 | T. Wu |
| 3 | 1st | 914546877×234772 − 1 | 10477 | 2010 | T. Wu |
| 4 | 1st | 119184698×5501# − 1 | 2354 | 2005 | J. Sun |
| 5 | 2nd | 45008010405×2621# + 1 | 1116 | 2010 | D. Broadhurst |
| 6 | 1st | 37488065464×1483# − 1 | 633 | 2010 | D. Augustin |
| 7 | 1st | 162597166369×827# − 1 | 356 | 2010 | D. Augustin |
| 8 | 2nd | 1148424905221×509# + 1 | 224 | 2010 | D. Augustin |
| 9 | 1st | 65728407627×431# − 1 | 185 | 2005 | D. Augustin |
| 10 | 2nd | 1070828503293×239# + 1 | 109 | 2009 | D. Augustin |
| 11 | 2nd | 2×13931865163581×127# + 1 | 63 | 2008 | D. Augustin |
| 12 | 2nd | 13931865163581×127# + 1 | 62 | 2008 | D. Augustin |
| 13 | 1st | 1753286498051×71# − 1 | 39 | 2005 | D. Augustin |
| 14 | 2nd | 335898524600734221050749906451371 | 33 | 2008 | J. K. Andersen |
| 15 | 2nd | 28320350134887132315879689643841 | 32 | 2008 | J. Wroblewski |
| 16 | 2nd | 2368823992523350998418445521 | 28 | 2008 | J. Wroblewski |
| 17 | 2nd | 1302312696655394336638441 | 25 | 2008 | J. Wroblewski |
q# denotes the primorial
Primorial
In mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than multiplying successive positive integers, only successive prime numbers are multiplied...
2×3×5×7×...×q.
, the longest known Cunningham chain of either kind is of length 17. The first known was of the 1st kind starting at 2759832934171386593519, discovered by Jaroslaw Wroblewski in 2008 where he also found some of the 2nd kind.
Congruences of Cunningham chains
Let the odd prime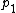 be the first prime of a Cunningham chain of the first kind. The first prime is odd, thus
be the first prime of a Cunningham chain of the first kind. The first prime is odd, thus 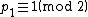 . Since each successive prime in the chain is
. Since each successive prime in the chain is 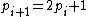 it follows that
it follows that 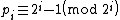 . Thus,
. Thus,  ,
, 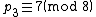 , and so forth.
, and so forth.The above property can be informally observed by considering the primes of a chain in base 2. (Note that, as with all bases, multiplying by the number of the base "shifts" the digits to the left.) When we consider
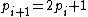 in base 2, we see that, by multiplying
in base 2, we see that, by multiplying 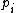 by 2, the least significant digit of
by 2, the least significant digit of 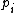 becomes the secondmost least significant digit of
becomes the secondmost least significant digit of  . Because
. Because 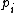 is odd--that is, the least significant digit is 1 in base 2--we know that the secondmost least significant digit of
is odd--that is, the least significant digit is 1 in base 2--we know that the secondmost least significant digit of 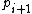 is also 1. And, finally, we can see that
is also 1. And, finally, we can see that 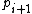 will be odd due to the addition of 1 to
will be odd due to the addition of 1 to 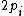 . In this way, successive primes in a Cunningham chain are essentially shifted left in binary with ones filling in the least significant digits. For example, here is a complete length 6 chain which starts at 141361469:
. In this way, successive primes in a Cunningham chain are essentially shifted left in binary with ones filling in the least significant digits. For example, here is a complete length 6 chain which starts at 141361469:| Binary | Decimal |
| 1000011011010000000100111101 | 141361469 |
| 10000110110100000001001111011 | 282722939 |
| 100001101101000000010011110111 | 565445879 |
| 1000011011010000000100111101111 | 1130891759 |
| 10000110110100000001001111011111 | 2261783519 |
| 100001101101000000010011110111111 | 4523567039 |
A similar result holds for Cunningham chains of the second kind. From the observation that
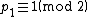 and the relation
and the relation 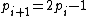 it follows that
it follows that  . In binary notation, the primes in a Cunningham chain of the second kind end with a pattern "0...01", where, for each
. In binary notation, the primes in a Cunningham chain of the second kind end with a pattern "0...01", where, for each 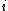 , the number of zeros in the pattern for
, the number of zeros in the pattern for 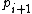 is one more than the number of zeros for
is one more than the number of zeros for  . As with Cunningham chains of the first kind, the bits left of the pattern shift left by one position with each successive prime.
. As with Cunningham chains of the first kind, the bits left of the pattern shift left by one position with each successive prime.External links
- The Prime Glossary: Cunningham chain
- PrimeLinks++: Cunningham chain
- Sequence A005602 in OEIS: the first term of the lowest complete Cunningham Chains of the first kind of length n, for 1 <= n <= 14
- Sequence A005603 in OEIS: the first term of the lowest complete Cunningham Chains of the second kind with length n, for 1 <= n <= 15

