RANSAC
Encyclopedia
RANSAC is an abbreviation for "RANdom SAmple Consensus". It is an iterative method
to estimate parameters of a mathematical model from a set of observed data which contains outliers. It is a non-deterministic algorithm in the sense that it produces a reasonable result only with a certain probability, with this probability increasing as more iterations are allowed. The algorithm was first published by Fischler and Bolles in 1981.
A basic assumption is that the data consists of "inliers", i.e., data whose distribution can be explained by some set of model parameters, and "outliers" which are data that do not fit the model. In addition to this, the data can be subject to noise. The outliers can come, e.g., from extreme values of the noise or from erroneous measurements or incorrect hypotheses about the interpretation of data. RANSAC also assumes that, given a (usually small) set of inliers, there exists a procedure which can estimate the parameters of a model that optimally explains or fits this data.
parameters.
RANSAC achieves its goal by iteratively selecting a random subset of the original data. These data are hypothetical inliers and this hypothesis is then tested as follows:
This procedure is repeated a fixed number of times, each time producing either a model which is rejected because too few points are classified as inliers or a refined model together with a corresponding error measure. In the latter case, we keep the refined model if its error is lower than the last saved model.
, works as follows:
input:
data - a set of observations
model - a model that can be fitted to data
n - the minimum number of data required to fit the model
k - the number of iterations performed by the algorithm
t - a threshold value for determining when a datum
fits a model
d - the number of close data values required to assert that a model fits well to data
output:
best_model - model parameters which best fit the data (or nil if no good model is found)
best_consensus_set - data points from which this model has been estimated
best_error - the error of this model relative to the data
iterations := 0
best_model := nil
best_consensus_set := nil
best_error := infinity
while iterations < k
maybe_inliers := n randomly selected values from data
maybe_model := model parameters fitted to maybe_inliers
consensus_set := maybe_inliers
for every point in data not in maybe_inliers
if point fits maybe_model with an error smaller than t
add point to consensus_set
if the number of elements in consensus_set is > d
(this implies that we may have found a good model,
now test how good it is)
this_model := model parameters fitted to all points in consensus_set
this_error := a measure of how well this_model fits these points
if this_error < best_error
(we have found a model which is better than any of the previous ones,
keep it until a better one is found)
best_model := this_model
best_consensus_set := consensus_set
best_error := this_error
increment iterations
return best_model, best_consensus_set, best_error
Possible variants of the RANSAC algorithm includes
w = number of inliers in data / number of points in data
A common case is that
is not well known beforehand, but some rough value can be given. Assuming that the n points needed for estimating a model are selected independently, 
is the probability that all n points are inliers and 
is the probability that at least one of the n points is an outlier, a case which implies that a bad model will be estimated from this point set. That probability to the power of k is the probability that the algorithm never selects a set of n points which all are inliers and this must be the same as 
. Consequently,
which, after taking the logarithm of both sides, leads to
This result assumes that the n data points are selected independently, that is, a point which has been selected once is replaced and can be selected again in the same iteration. This is often not a reasonable approach and the derived value for k should be taken as an upper limit in the case that the points are selected without replacement. For example, in the case of finding a line which fits the data set illustrated in the above figure, the RANSAC algorithm typically chooses 2 points in each iteration and computes
To gain additional confidence, the standard deviation
or multiples thereof can be added to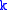
. The standard deviation of 
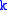is defined as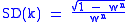
of the model parameters, i.e., it can estimate the parameters with a high degree of accuracy even when a significant number of outliers
are present in the data set. A disadvantage of RANSAC is that there is no upper bound on the time it takes to compute these parameters. When the number of iterations computed is limited the solution obtained may not be optimal, and it may not even be one that fits the data in a good way. In this way RANSAC offers a trade-off; by computing a greater number of iterations the probability of a reasonable model being produced is increased. Another disadvantage of RANSAC is that it requires the setting of problem-specific thresholds.
RANSAC can only estimate one model for a particular data set. As for any one-model approach when two (or more) model instances exist, RANSAC may fail to find either one. The Hough transform
is an alternative robust estimation technique that may be useful when more than one model instance is present.
, e.g., to simultaneously solve the correspondence problem
and estimate the fundamental matrix related to a pair of stereo cameras.
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
to estimate parameters of a mathematical model from a set of observed data which contains outliers. It is a non-deterministic algorithm in the sense that it produces a reasonable result only with a certain probability, with this probability increasing as more iterations are allowed. The algorithm was first published by Fischler and Bolles in 1981.
A basic assumption is that the data consists of "inliers", i.e., data whose distribution can be explained by some set of model parameters, and "outliers" which are data that do not fit the model. In addition to this, the data can be subject to noise. The outliers can come, e.g., from extreme values of the noise or from erroneous measurements or incorrect hypotheses about the interpretation of data. RANSAC also assumes that, given a (usually small) set of inliers, there exists a procedure which can estimate the parameters of a model that optimally explains or fits this data.
Example
A simple example is fitting of a 2D line to a set of observations. Assuming that this set contains both inliers, i.e., points which approximately can be fitted to a line, and outliers, points which cannot be fitted to this line, a simple least squares method for line fitting will in general produce a line with a bad fit to the inliers. The reason is that it is optimally fitted to all points, including the outliers. RANSAC, on the other hand, can produce a model which is only computed from the inliers, provided that the probability of choosing only inliers in the selection of data is sufficiently high. There is no guarantee for this situation, however, and there are a number of algorithm parameters which must be carefully chosen to keep the level of probability reasonably high.Overview
The input to the RANSAC algorithm is a set of observed data values, a parameterized model which can explain or be fitted to the observations, and some confidenceConfidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
parameters.
RANSAC achieves its goal by iteratively selecting a random subset of the original data. These data are hypothetical inliers and this hypothesis is then tested as follows:
- A model is fitted to the hypothetical inliers, i.e. all free parameters of the model are reconstructed from the inliers.
- All other data are then tested against the fitted model and, if a point fits well to the estimated model, also considered as a hypothetical inlier.
- The estimated model is reasonably good if sufficiently many points have been classified as hypothetical inliers.
- The model is reestimated from all hypothetical inliers, because it has only been estimated from the initial set of hypothetical inliers.
- Finally, the model is evaluated by estimating the error of the inliers relative to the model.
This procedure is repeated a fixed number of times, each time producing either a model which is rejected because too few points are classified as inliers or a refined model together with a corresponding error measure. In the latter case, we keep the refined model if its error is lower than the last saved model.
The algorithm
The generic RANSAC algorithm, in pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
, works as follows:
input:
data - a set of observations
model - a model that can be fitted to data
n - the minimum number of data required to fit the model
k - the number of iterations performed by the algorithm
t - a threshold value for determining when a datum
Datum
A geodetic datum is a reference from which measurements are made. In surveying and geodesy, a datum is a set of reference points on the Earth's surface against which position measurements are made, and an associated model of the shape of the earth to define a geographic coordinate system...
fits a model
d - the number of close data values required to assert that a model fits well to data
output:
best_model - model parameters which best fit the data (or nil if no good model is found)
best_consensus_set - data points from which this model has been estimated
best_error - the error of this model relative to the data
iterations := 0
best_model := nil
best_consensus_set := nil
best_error := infinity
while iterations < k
maybe_inliers := n randomly selected values from data
maybe_model := model parameters fitted to maybe_inliers
consensus_set := maybe_inliers
for every point in data not in maybe_inliers
if point fits maybe_model with an error smaller than t
add point to consensus_set
if the number of elements in consensus_set is > d
(this implies that we may have found a good model,
now test how good it is)
this_model := model parameters fitted to all points in consensus_set
this_error := a measure of how well this_model fits these points
if this_error < best_error
(we have found a model which is better than any of the previous ones,
keep it until a better one is found)
best_model := this_model
best_consensus_set := consensus_set
best_error := this_error
increment iterations
return best_model, best_consensus_set, best_error
Possible variants of the RANSAC algorithm includes
- Break the main loop if a sufficiently good model has been found, that is, one with sufficiently small error. May save some computation time at the expense of an additional parameter.
- Compute
this_errordirectly frommaybe_modelwithout re-estimating a model from the consensus set. May save some time at the expense of comparing errors related to models which are estimated from a small number of points and therefore more sensitive to noise.
The parameters
The values of parameters t and d have to be determined from specific requirements related to the application and the data set, possibly based on experimental evaluation. The parameter k (the number of iterations), however, can be determined from a theoretical result. Let p be the probability that the RANSAC algorithm in some iteration selects only inliers from the input data set when it chooses the n points from which the model parameters are estimated. When this happens, the resulting model is likely to be useful so p gives the probability that the algorithm produces a useful result. Let w be the probability of choosing an inlier each time a single point is selected, that is,w = number of inliers in data / number of points in data
A common case is that
is not well known beforehand, but some rough value can be given. Assuming that the n points needed for estimating a model are selected independently, is the probability that all n points are inliers and is the probability that at least one of the n points is an outlier, a case which implies that a bad model will be estimated from this point set. That probability to the power of k is the probability that the algorithm never selects a set of n points which all are inliers and this must be the same as . Consequently,which, after taking the logarithm of both sides, leads to
This result assumes that the n data points are selected independently, that is, a point which has been selected once is replaced and can be selected again in the same iteration. This is often not a reasonable approach and the derived value for k should be taken as an upper limit in the case that the points are selected without replacement. For example, in the case of finding a line which fits the data set illustrated in the above figure, the RANSAC algorithm typically chooses 2 points in each iteration and computes
maybe_model as the line between the points and it is then critical that the two points are distinct.To gain additional confidence, the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
or multiples thereof can be added to
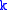. The standard deviation of 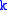is defined as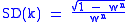Advantages and disadvantages
An advantage of RANSAC is its ability to do robust estimationRobust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
of the model parameters, i.e., it can estimate the parameters with a high degree of accuracy even when a significant number of outliers
Outlier
In statistics, an outlier is an observation that is numerically distant from the rest of the data. Grubbs defined an outlier as: An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs....
are present in the data set. A disadvantage of RANSAC is that there is no upper bound on the time it takes to compute these parameters. When the number of iterations computed is limited the solution obtained may not be optimal, and it may not even be one that fits the data in a good way. In this way RANSAC offers a trade-off; by computing a greater number of iterations the probability of a reasonable model being produced is increased. Another disadvantage of RANSAC is that it requires the setting of problem-specific thresholds.
RANSAC can only estimate one model for a particular data set. As for any one-model approach when two (or more) model instances exist, RANSAC may fail to find either one. The Hough transform
Hough transform
The Hough transform is a feature extraction technique used in image analysis, computer vision, and digital image processing. The purpose of the technique is to find imperfect instances of objects within a certain class of shapes by a voting procedure...
is an alternative robust estimation technique that may be useful when more than one model instance is present.
Applications
The RANSAC algorithm is often used in computer visionComputer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, e.g., to simultaneously solve the correspondence problem
Correspondence problem
The correspondence problem tries to figure out which parts of an image correspond to which parts of another image, after the camera has moved, time has elapsed, and/or the objects have moved around.-Overview:...
and estimate the fundamental matrix related to a pair of stereo cameras.
External links
- RANSAC Toolbox for MATLAB. A research (and didactic) oriented toolbox to explore the RANSAC algorithm in MATLABMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
. It is highly configurable and contains the routines to solve a few relevant estimation problems. - Implementation in C++ as a generic template.
- RANSAC for Dummies A simple tutorial with many examples that uses the RANSAC Toolbox for MATLAB.
- 25 Years of RANSAC Workshop
- http://www.csse.uwa.edu.au/~pk/Research/MatlabFns/#robustSource code for RANSAC in MATLABMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
]