
Pfister form
Encyclopedia
In mathematics
, a Pfister form is a particular kind of quadratic form
over a field
F (whose characteristic
is usually assumed to be not 2), introduced by A. Pfister in 1965. A Pfister form is in 2n variables, for some natural number n (also called an n-Pfister form), and may be written as a tensor product of quadratic forms
as:
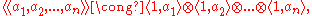
for ai elements of the field F. An n-Pfister form may also be constructed inductively from an n-1-Pfister form q and an a in F, as .
.
So all 1-Pfister forms and 2-Pfister forms look like:
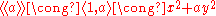 .
.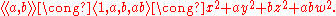
n-Pfister forms for n ≤ 3 are norm form
s of composition algebra
s. In fact, in this case, two n-Pfister forms are isometric
if and only if the corresponding composition algebras are isomorphic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Pfister form is a particular kind of quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F (whose characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
is usually assumed to be not 2), introduced by A. Pfister in 1965. A Pfister form is in 2n variables, for some natural number n (also called an n-Pfister form), and may be written as a tensor product of quadratic forms
Tensor product of quadratic forms
The tensor product of quadratic forms is most easily understood when one views the quadratic forms as quadratic spaces. So, if and are quadratic spaces, which V,W vector spaces, then the tensor product is a quadratic form q on the tensor product of vector spaces V \otimes W.It is defined in such...
as:
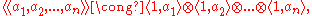
for ai elements of the field F. An n-Pfister form may also be constructed inductively from an n-1-Pfister form q and an a in F, as
 .
.So all 1-Pfister forms and 2-Pfister forms look like:
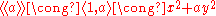 .
.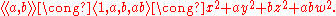
n-Pfister forms for n ≤ 3 are norm form
Norm form
In mathematics, a norm form is a homogeneous form in n variables constructed from the field norm of a field extension L/K of degree n...
s of composition algebra
Composition algebra
In mathematics, a composition algebra A over a field K is a unital algebra over K together with a nondegenerate quadratic form N which satisfiesN = NN\,...
s. In fact, in this case, two n-Pfister forms are isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
if and only if the corresponding composition algebras are isomorphic.

