
Extremal length
Encyclopedia
In the mathematical
theory of conformal and quasiconformal mapping
s, the extremal length of a collection of curve
s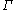 is a conformal invariant of
is a conformal invariant of 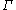 . More specifically, suppose that
. More specifically, suppose that
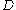 is an open set in the complex plane
is an open set in the complex plane
and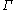 is a collection
is a collection
of paths in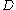 and
and 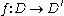 is a conformal mapping. Then the extremal length of
is a conformal mapping. Then the extremal length of 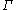 is equal to the extremal length of the image of
is equal to the extremal length of the image of 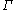 under
under 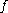 . For this reason, the extremal length is a useful tool in the study of conformal mappings. Extremal length can also be useful in dimensions greater than two,
. For this reason, the extremal length is a useful tool in the study of conformal mappings. Extremal length can also be useful in dimensions greater than two,
but the following deals primarily with the two dimensional setting.
Let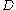 be an open set in the complex plane. Suppose that
be an open set in the complex plane. Suppose that 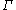 is a
is a
collection of rectifiable curves in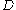 . If
. If 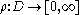
is Borel-measurable
, then for any rectifiable curve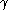 we let
we let

denote the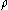 -length of
-length of 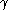 , where
, where 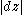 denotes the
denotes the
Euclidean
element of length. (It is possible that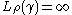 .)
.)
What does this really mean?
If is parameterized in some interval
is parameterized in some interval 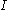 ,
,
then is the integral of the Borel-measurable function
is the integral of the Borel-measurable function
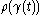 with respect to the Borel measure on
with respect to the Borel measure on 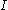
for which the measure of every subinterval is the length of the
is the length of the
restriction of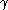 to
to 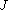 . In other words, it is the
. In other words, it is the
Lebesgue-Stieltjes integral
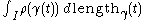 , where
, where
 is the length of the restriction of
is the length of the restriction of 
to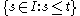 .
.
Also set
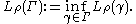
The area of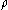 is defined as
is defined as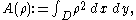
and the extremal length of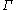 is
is
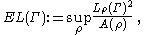
where the supremum is over all Borel-measureable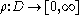 with
with 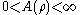 . If
. If 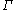 contains some non-rectifiable curves and
contains some non-rectifiable curves and
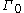 denotes the set of rectifiable curves in
denotes the set of rectifiable curves in 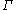 , then
, then
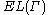 is defined to be
is defined to be 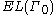 .
.
The term modulus of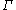 refers to
refers to 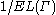 .
.
The extremal distance in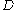 between two sets in
between two sets in 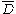 is the extremal length of the collection of curves in
is the extremal length of the collection of curves in 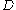 with one endpoint in one set and the other endpoint in the other set.
with one endpoint in one set and the other endpoint in the other set.
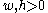 , and let
, and let 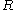 be the rectangle
be the rectangle
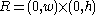 . Let
. Let 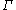 be the set of all finite
be the set of all finite
length curves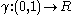 that cross the rectangle left to right,
that cross the rectangle left to right,
in the sense that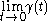
is on the left edge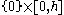 of the rectangle, and
of the rectangle, and
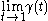 is on the right edge
is on the right edge 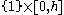 .
.
(The limits necessarily exist, because we are assuming that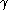
has finite length.) We will now prove that in this case
First, we may take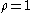 on
on 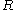 . This
. This 
gives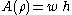 and
and 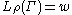 . The definition
. The definition
of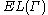 as a supremum then gives
as a supremum then gives 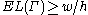 .
.
The opposite inequality is not quite so easy. Consider an arbitrary
Borel-measurable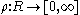 such that
such that
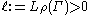 .
.
For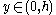 , let
, let 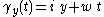
(where we are identifying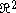 with the complex plane).
with the complex plane).
Then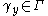 , and hence
, and hence  .
.
The latter inequality may be written as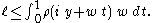
Integrating this inequality over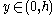 implies
implies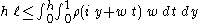 .
.
Now a change of variable and an application of the Cauchy-Schwarz inequality give
and an application of the Cauchy-Schwarz inequality give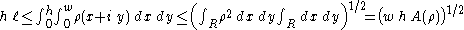 . This gives
. This gives 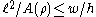 .
.
Therefore,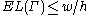 , as required.
, as required.
As the proof shows, the extremal length of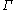 is the same as the extremal
is the same as the extremal
length of the much smaller collection of curves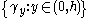 .
.
It should be pointed out that the extremal length of the family of curves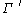
that connect the bottom edge of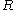 to the top edge of
to the top edge of 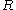 satisfies
satisfies
 , by the same argument. Therefore,
, by the same argument. Therefore, 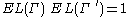 .
.
It is natural to refer to this as a duality property of extremal length, and a similar duality property
occurs in the context of the next subsection. Observe that obtaining a lower bound on
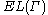 is generally easier than obtaining an upper bound, since the lower bound involves
is generally easier than obtaining an upper bound, since the lower bound involves
choosing a reasonably good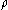 and estimating
and estimating 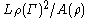 ,
,
while the upper bound involves proving a statement about all possible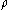 . For this reason,
. For this reason,
duality is often useful when it can be established: when we know that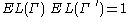 ,
,
a lower bound on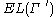 translates to an upper bound on
translates to an upper bound on 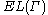 .
.
 and
and 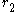 be two radii satisfying
be two radii satisfying
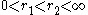 . Let
. Let 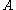 be the
be the
annulus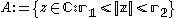 and let
and let
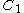 and
and 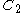 be the two boundary components
be the two boundary components
of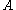 :
: 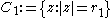
and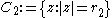 . Consider the extremal distance
. Consider the extremal distance
in between
between 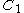 and
and 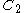 ;
;
which is the extremal length of the collection of
of
curves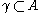 connecting
connecting 
and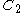 .
.
To obtain an lower bound on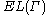 ,
,
we take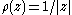 . Then for
. Then for 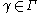
oriented from to
to 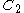
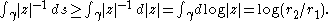
On the other hand,
We conclude that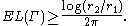
We now see that this inequality is really an equality by employing an argument similar to the one given above for the rectangle. Consider an arbitrary Borel-measurable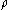 such that
such that 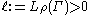 . For
. For  let
let 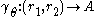 denote the curve
denote the curve 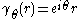 . Then
. Then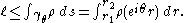
We integrate over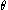 and apply the Cauchy-Schwarz inequality, to obtain:
and apply the Cauchy-Schwarz inequality, to obtain: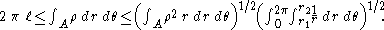
Squaring gives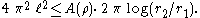
This implies the upper bound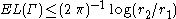 .
.
When combined with the lower bound, this yields the exact value of the extremal length: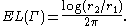
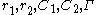 and
and  be as above, but now let
be as above, but now let 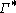 be the collection of all curves that wind once around the annulus, separating
be the collection of all curves that wind once around the annulus, separating 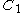 from
from 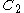 . Using the above methods, it is not hard to show that
. Using the above methods, it is not hard to show that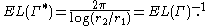
This illustrates another instance of extremal length duality.
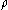 which maximized the
which maximized the
ratio and gave the extremal length corresponded to a flat metric. In other words, when the Euclidean
and gave the extremal length corresponded to a flat metric. In other words, when the Euclidean
Riemannian metric of the corresponding planar domain is scaled by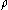 , the resulting metric is flat. In the case of the rectangle, this was just the original metric, but for the annulus, the extremal metric identified is the metric of a cylinder
, the resulting metric is flat. In the case of the rectangle, this was just the original metric, but for the annulus, the extremal metric identified is the metric of a cylinder
. We now discuss an example where an extremal metric is not flat. The projective plane with the spherical metric is obtained by identifying antipodal point
s on the unit sphere in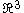 with its Riemannian spherical metric. In other words, this is the quotient of the sphere by the map
with its Riemannian spherical metric. In other words, this is the quotient of the sphere by the map 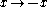 . Let
. Let 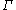 denote the set of closed curves in this projective plane that are not null-homotopic. (Each curve in
denote the set of closed curves in this projective plane that are not null-homotopic. (Each curve in 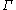 is obtained by projecting a curve on the sphere from a point to its antipode.) Then the spherical metric is extremal for this curve family. (The definition of extremal length readily extends to Riemannian surfaces.) Thus, the extremal length is
is obtained by projecting a curve on the sphere from a point to its antipode.) Then the spherical metric is extremal for this curve family. (The definition of extremal length readily extends to Riemannian surfaces.) Thus, the extremal length is 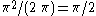 .
.
 is any collection of paths all of which have positive diameter and containing a point
is any collection of paths all of which have positive diameter and containing a point 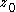 , then
, then 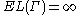 . This follows, for example, by taking
. This follows, for example, by taking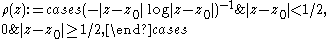
which satisfies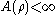 and
and 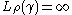 for every rectifiable
for every rectifiable 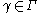 .
.
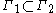 , then
, then  .
.
Moreover, the same conclusion holds if every curve contains a curve
contains a curve 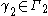 as a subcurve (that is,
as a subcurve (that is, 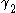 is the restriction of
is the restriction of 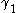 to a subinterval of its domain). Another sometimes useful inequality is
to a subinterval of its domain). Another sometimes useful inequality is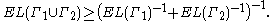
This is clear if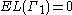 or if
or if 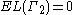 , in which case the right hand side is interpreted as
, in which case the right hand side is interpreted as 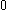 . So suppose that this is not the case and with no loss of generality assume that the curves in
. So suppose that this is not the case and with no loss of generality assume that the curves in  are all rectifiable. Let
are all rectifiable. Let  satisfy
satisfy  for
for 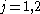 . Set
. Set 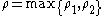 . Then
. Then 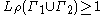 and
and 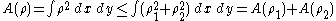 , which proves the inequality.
, which proves the inequality.
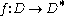 be a conformal
be a conformal
homeomorphism
(a bijective holomorphic map) between planar domains. Suppose that
 is a collection of curves in
is a collection of curves in 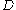 ,
,
and let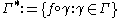 denote the
denote the
image curves under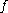 . Then
. Then 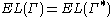 .
.
This conformal invariance statement is the primary reason why the concept of
extremal length is useful.
Here is a proof of conformal invariance. Let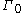 denote the set of curves
denote the set of curves
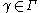 such that
such that 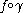 is rectifiable, and let
is rectifiable, and let
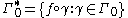 , which is the set of rectifiable
, which is the set of rectifiable
curves in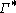 . Suppose that
. Suppose that 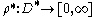 is Borel-measurable. Define
is Borel-measurable. Define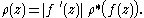
A change of variables gives
gives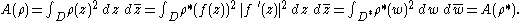
Now suppose that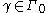 is rectifiable, and set
is rectifiable, and set 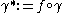 . Formally, we may use a change of variables again:
. Formally, we may use a change of variables again:
To justify this formal calculation, suppose that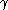 is defined in some interval
is defined in some interval 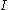 , let
, let
 denote the length of the restriction of
denote the length of the restriction of 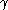 to
to 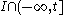 ,
,
and let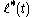 be similarly defined with
be similarly defined with 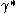 in place of
in place of  . Then it is easy to see that
. Then it is easy to see that 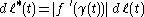 , and this implies
, and this implies  , as required. The above equalities give,
, as required. The above equalities give,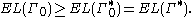
If we knew that each curve in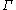 and
and  was rectifiable, this would
was rectifiable, this would
prove since we may also apply the above with
since we may also apply the above with 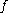 replaced by its inverse
replaced by its inverse
and interchanged with
interchanged with 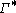 . It remains to handle the non-rectifiable curves.
. It remains to handle the non-rectifiable curves.
Now let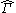 denote the set of rectifiable curves
denote the set of rectifiable curves 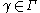 such that
such that 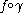 is
is
non-rectifiable. We claim that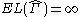 .
.
Indeed, take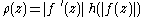 , where
, where 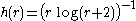 .
.
Then a change of variable as above gives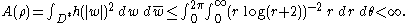
For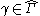 and
and 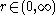 such that
such that 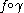
is contained in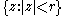 , we have
, we have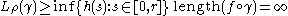 .
.
On the other hand, suppose that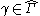 is such that
is such that 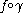 is unbounded.
is unbounded.
Set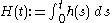 . Then
. Then
 is at least the length of the curve
is at least the length of the curve 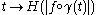
(from an interval in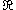 to
to 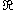 ). Since
). Since 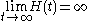 ,
,
it follows that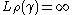 .
.
Thus, indeed,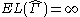 .
.
Using the results of the previous section, we have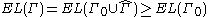 .
.
We have already seen that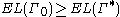 . Thus,
. Thus, 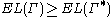 .
.
The reverse inequality holds by symmetry, and conformal invariance is therefore established.
By the calculation of the extremal distance in an annulus and the conformal
invariance it follows that the annulus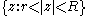 (where
(where 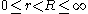 )
)
is not conformally homeomorphic to the annulus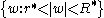 if
if 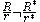 .
.
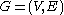 is some graph
is some graph
and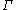 is a collection of paths in
is a collection of paths in 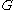 . There are two variants of extremal length in this setting. To define the edge extremal length, originally introduced by R. J. Duffin, consider a function
. There are two variants of extremal length in this setting. To define the edge extremal length, originally introduced by R. J. Duffin, consider a function 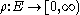 . The
. The 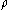 -length of a path is defined as the sum of
-length of a path is defined as the sum of 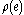 over all edges in the path, counted with multiplicity. The "area"
over all edges in the path, counted with multiplicity. The "area" 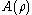 is defined as
is defined as 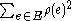 . The extremal length of
. The extremal length of 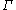 is then defined as before. If
is then defined as before. If 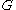 is interpreted as a resistor network, where each edge has unit resistance, then the effective resistance between two sets of veritces is precisely the edge extremal length of the collection of paths with one endpoint in one set and the other endpoint in the other set. Thus, discrete extremal length is useful for estimates in discrete potential theory
is interpreted as a resistor network, where each edge has unit resistance, then the effective resistance between two sets of veritces is precisely the edge extremal length of the collection of paths with one endpoint in one set and the other endpoint in the other set. Thus, discrete extremal length is useful for estimates in discrete potential theory
.
Another notion of discrete extremal length that is appropriate in other contexts is vertex extremal length, where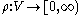 , the area is
, the area is 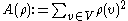 , and the length of a path is the sum of
, and the length of a path is the sum of  over the vertices visited by the path, with multiplicity.
over the vertices visited by the path, with multiplicity.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
theory of conformal and quasiconformal mapping
Quasiconformal mapping
In mathematical complex analysis, a quasiconformal mapping, introduced by and named by , is a homeomorphism between plane domains which to first order takes small circles to small ellipses of bounded eccentricity....
s, the extremal length of a collection of curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s
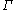 is a conformal invariant of
is a conformal invariant of 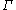 . More specifically, suppose that
. More specifically, suppose that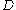 is an open set in the complex plane
is an open set in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
and
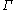 is a collection
is a collectionof paths in
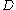 and
and 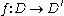 is a conformal mapping. Then the extremal length of
is a conformal mapping. Then the extremal length of 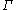 is equal to the extremal length of the image of
is equal to the extremal length of the image of 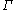 under
under 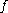 . For this reason, the extremal length is a useful tool in the study of conformal mappings. Extremal length can also be useful in dimensions greater than two,
. For this reason, the extremal length is a useful tool in the study of conformal mappings. Extremal length can also be useful in dimensions greater than two,but the following deals primarily with the two dimensional setting.
Definition of extremal length
To define extremal length, we need to first introduce several related quantities.Let
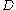 be an open set in the complex plane. Suppose that
be an open set in the complex plane. Suppose that 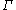 is a
is acollection of rectifiable curves in
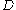 . If
. If 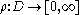
is Borel-measurable
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
, then for any rectifiable curve
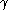 we let
we let
denote the
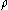 -length of
-length of 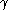 , where
, where 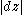 denotes the
denotes theEuclidean
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
element of length. (It is possible that
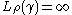 .)
.)What does this really mean?
If
 is parameterized in some interval
is parameterized in some interval 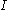 ,
,then
 is the integral of the Borel-measurable function
is the integral of the Borel-measurable function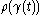 with respect to the Borel measure on
with respect to the Borel measure on 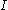
for which the measure of every subinterval
 is the length of the
is the length of therestriction of
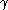 to
to 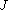 . In other words, it is the
. In other words, it is theLebesgue-Stieltjes integral
Lebesgue-Stieltjes integration
In measure-theoretic analysis and related branches of mathematics, Lebesgue–Stieltjes integration generalizes Riemann–Stieltjes and Lebesgue integration, preserving the many advantages of the former in a more general measure-theoretic framework...
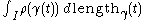 , where
, where is the length of the restriction of
is the length of the restriction of 
to
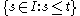 .
.Also set
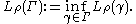
The area of
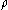 is defined as
is defined as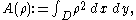
and the extremal length of
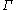 is
is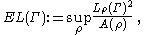
where the supremum is over all Borel-measureable
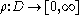 with
with 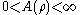 . If
. If 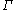 contains some non-rectifiable curves and
contains some non-rectifiable curves and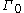 denotes the set of rectifiable curves in
denotes the set of rectifiable curves in 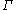 , then
, then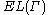 is defined to be
is defined to be 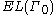 .
.The term modulus of
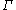 refers to
refers to 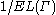 .
.The extremal distance in
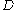 between two sets in
between two sets in 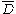 is the extremal length of the collection of curves in
is the extremal length of the collection of curves in 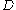 with one endpoint in one set and the other endpoint in the other set.
with one endpoint in one set and the other endpoint in the other set.Examples
In this section the extremal length is calculated in several examples. The first three of these examples are actually useful in applications of extremal length.Extremal distance in rectangle
Fix some positive numbers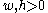 , and let
, and let 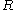 be the rectangle
be the rectangle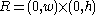 . Let
. Let 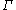 be the set of all finite
be the set of all finitelength curves
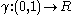 that cross the rectangle left to right,
that cross the rectangle left to right,in the sense that
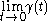
is on the left edge
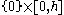 of the rectangle, and
of the rectangle, and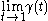 is on the right edge
is on the right edge 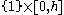 .
.(The limits necessarily exist, because we are assuming that
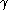
has finite length.) We will now prove that in this case

First, we may take
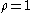 on
on 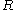 . This
. This 
gives
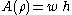 and
and 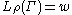 . The definition
. The definitionof
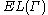 as a supremum then gives
as a supremum then gives 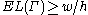 .
.The opposite inequality is not quite so easy. Consider an arbitrary
Borel-measurable
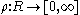 such that
such that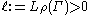 .
.For
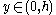 , let
, let 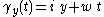
(where we are identifying
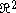 with the complex plane).
with the complex plane).Then
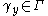 , and hence
, and hence  .
.The latter inequality may be written as
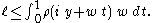
Integrating this inequality over
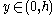 implies
implies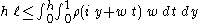 .
.Now a change of variable
 and an application of the Cauchy-Schwarz inequality give
and an application of the Cauchy-Schwarz inequality give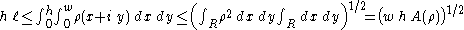 . This gives
. This gives 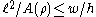 .
.Therefore,
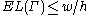 , as required.
, as required.As the proof shows, the extremal length of
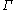 is the same as the extremal
is the same as the extremallength of the much smaller collection of curves
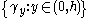 .
.It should be pointed out that the extremal length of the family of curves
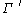
that connect the bottom edge of
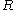 to the top edge of
to the top edge of 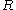 satisfies
satisfies , by the same argument. Therefore,
, by the same argument. Therefore, 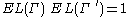 .
.It is natural to refer to this as a duality property of extremal length, and a similar duality property
occurs in the context of the next subsection. Observe that obtaining a lower bound on
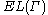 is generally easier than obtaining an upper bound, since the lower bound involves
is generally easier than obtaining an upper bound, since the lower bound involveschoosing a reasonably good
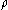 and estimating
and estimating 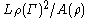 ,
,while the upper bound involves proving a statement about all possible
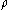 . For this reason,
. For this reason,duality is often useful when it can be established: when we know that
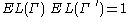 ,
,a lower bound on
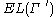 translates to an upper bound on
translates to an upper bound on 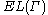 .
.Extremal distance in annulus
Let and
and 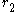 be two radii satisfying
be two radii satisfying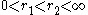 . Let
. Let 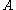 be the
be theannulus
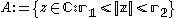 and let
and let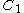 and
and 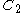 be the two boundary components
be the two boundary componentsof
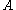 :
: 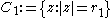
and
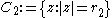 . Consider the extremal distance
. Consider the extremal distancein
 between
between 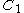 and
and 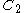 ;
;which is the extremal length of the collection
 of
ofcurves
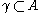 connecting
connecting 
and
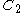 .
.To obtain an lower bound on
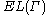 ,
,we take
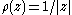 . Then for
. Then for 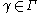
oriented from
 to
to 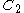
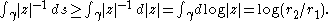
On the other hand,

We conclude that
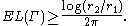
We now see that this inequality is really an equality by employing an argument similar to the one given above for the rectangle. Consider an arbitrary Borel-measurable
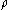 such that
such that 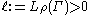 . For
. For  let
let 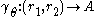 denote the curve
denote the curve 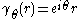 . Then
. Then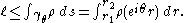
We integrate over
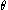 and apply the Cauchy-Schwarz inequality, to obtain:
and apply the Cauchy-Schwarz inequality, to obtain: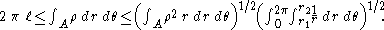
Squaring gives
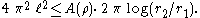
This implies the upper bound
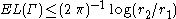 .
.When combined with the lower bound, this yields the exact value of the extremal length:
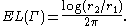
Extremal length around an annulus
Let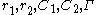 and
and  be as above, but now let
be as above, but now let 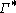 be the collection of all curves that wind once around the annulus, separating
be the collection of all curves that wind once around the annulus, separating 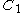 from
from 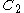 . Using the above methods, it is not hard to show that
. Using the above methods, it is not hard to show that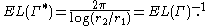
This illustrates another instance of extremal length duality.
Extremal length of topologically essential paths in projective plane
In the above examples, the extremal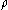 which maximized the
which maximized theratio
 and gave the extremal length corresponded to a flat metric. In other words, when the Euclidean
and gave the extremal length corresponded to a flat metric. In other words, when the EuclideanEuclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
Riemannian metric of the corresponding planar domain is scaled by
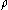 , the resulting metric is flat. In the case of the rectangle, this was just the original metric, but for the annulus, the extremal metric identified is the metric of a cylinder
, the resulting metric is flat. In the case of the rectangle, this was just the original metric, but for the annulus, the extremal metric identified is the metric of a cylinderCylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
. We now discuss an example where an extremal metric is not flat. The projective plane with the spherical metric is obtained by identifying antipodal point
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
s on the unit sphere in
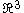 with its Riemannian spherical metric. In other words, this is the quotient of the sphere by the map
with its Riemannian spherical metric. In other words, this is the quotient of the sphere by the map 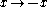 . Let
. Let 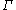 denote the set of closed curves in this projective plane that are not null-homotopic. (Each curve in
denote the set of closed curves in this projective plane that are not null-homotopic. (Each curve in 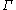 is obtained by projecting a curve on the sphere from a point to its antipode.) Then the spherical metric is extremal for this curve family. (The definition of extremal length readily extends to Riemannian surfaces.) Thus, the extremal length is
is obtained by projecting a curve on the sphere from a point to its antipode.) Then the spherical metric is extremal for this curve family. (The definition of extremal length readily extends to Riemannian surfaces.) Thus, the extremal length is 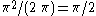 .
.Extremal length of paths containing a point
If is any collection of paths all of which have positive diameter and containing a point
is any collection of paths all of which have positive diameter and containing a point 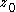 , then
, then 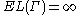 . This follows, for example, by taking
. This follows, for example, by taking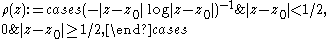
which satisfies
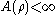 and
and 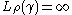 for every rectifiable
for every rectifiable 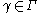 .
.Elementary properties of extremal length
The extremal length satisfies a few simple monotonicity properties. First, it is clear that if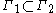 , then
, then  .
.Moreover, the same conclusion holds if every curve
 contains a curve
contains a curve 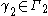 as a subcurve (that is,
as a subcurve (that is, 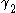 is the restriction of
is the restriction of 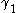 to a subinterval of its domain). Another sometimes useful inequality is
to a subinterval of its domain). Another sometimes useful inequality is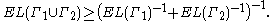
This is clear if
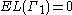 or if
or if 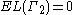 , in which case the right hand side is interpreted as
, in which case the right hand side is interpreted as 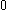 . So suppose that this is not the case and with no loss of generality assume that the curves in
. So suppose that this is not the case and with no loss of generality assume that the curves in  are all rectifiable. Let
are all rectifiable. Let  satisfy
satisfy  for
for 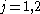 . Set
. Set 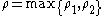 . Then
. Then 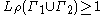 and
and 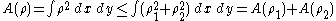 , which proves the inequality.
, which proves the inequality.Conformal invariance of extremal length
Let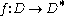 be a conformal
be a conformalConformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
(a bijective holomorphic map) between planar domains. Suppose that
 is a collection of curves in
is a collection of curves in 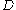 ,
,and let
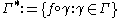 denote the
denote theimage curves under
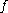 . Then
. Then 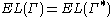 .
.This conformal invariance statement is the primary reason why the concept of
extremal length is useful.
Here is a proof of conformal invariance. Let
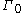 denote the set of curves
denote the set of curves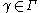 such that
such that 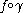 is rectifiable, and let
is rectifiable, and let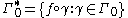 , which is the set of rectifiable
, which is the set of rectifiablecurves in
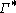 . Suppose that
. Suppose that 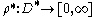 is Borel-measurable. Define
is Borel-measurable. Define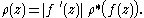
A change of variables
 gives
gives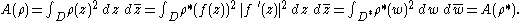
Now suppose that
 is rectifiable, and set
is rectifiable, and set 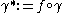 . Formally, we may use a change of variables again:
. Formally, we may use a change of variables again:
To justify this formal calculation, suppose that
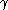 is defined in some interval
is defined in some interval 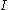 , let
, let denote the length of the restriction of
denote the length of the restriction of 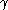 to
to 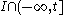 ,
,and let
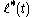 be similarly defined with
be similarly defined with 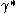 in place of
in place of  . Then it is easy to see that
. Then it is easy to see that 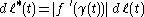 , and this implies
, and this implies  , as required. The above equalities give,
, as required. The above equalities give,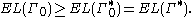
If we knew that each curve in
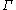 and
and  was rectifiable, this would
was rectifiable, this wouldprove
 since we may also apply the above with
since we may also apply the above with 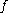 replaced by its inverse
replaced by its inverseand
 interchanged with
interchanged with 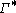 . It remains to handle the non-rectifiable curves.
. It remains to handle the non-rectifiable curves.Now let
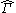 denote the set of rectifiable curves
denote the set of rectifiable curves 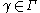 such that
such that 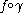 is
isnon-rectifiable. We claim that
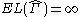 .
.Indeed, take
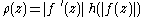 , where
, where 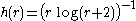 .
.Then a change of variable as above gives
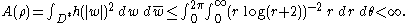
For
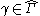 and
and 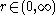 such that
such that 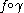
is contained in
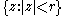 , we have
, we have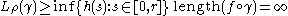 .
.On the other hand, suppose that
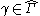 is such that
is such that 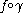 is unbounded.
is unbounded.Set
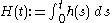 . Then
. Then is at least the length of the curve
is at least the length of the curve 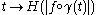
(from an interval in
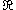 to
to 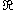 ). Since
). Since 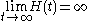 ,
,it follows that
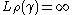 .
.Thus, indeed,
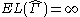 .
.Using the results of the previous section, we have
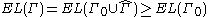 .
.We have already seen that
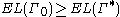 . Thus,
. Thus, 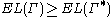 .
.The reverse inequality holds by symmetry, and conformal invariance is therefore established.
Some applications of extremal length
By the calculation of the extremal distance in an annulus and the conformal
invariance it follows that the annulus
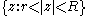 (where
(where 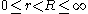 )
)is not conformally homeomorphic to the annulus
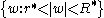 if
if 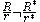 .
.Extremal length in higher dimensions
The notion of extremal length adapts to the study of various problems in dimensions 3 and higher, especially in relation to quasiconformal mappings.Discrete extremal length
Suppose that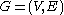 is some graph
is some graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
and
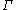 is a collection of paths in
is a collection of paths in 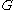 . There are two variants of extremal length in this setting. To define the edge extremal length, originally introduced by R. J. Duffin, consider a function
. There are two variants of extremal length in this setting. To define the edge extremal length, originally introduced by R. J. Duffin, consider a function 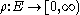 . The
. The 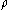 -length of a path is defined as the sum of
-length of a path is defined as the sum of 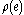 over all edges in the path, counted with multiplicity. The "area"
over all edges in the path, counted with multiplicity. The "area" 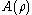 is defined as
is defined as 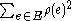 . The extremal length of
. The extremal length of 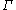 is then defined as before. If
is then defined as before. If 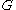 is interpreted as a resistor network, where each edge has unit resistance, then the effective resistance between two sets of veritces is precisely the edge extremal length of the collection of paths with one endpoint in one set and the other endpoint in the other set. Thus, discrete extremal length is useful for estimates in discrete potential theory
is interpreted as a resistor network, where each edge has unit resistance, then the effective resistance between two sets of veritces is precisely the edge extremal length of the collection of paths with one endpoint in one set and the other endpoint in the other set. Thus, discrete extremal length is useful for estimates in discrete potential theoryPotential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
.
Another notion of discrete extremal length that is appropriate in other contexts is vertex extremal length, where
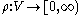 , the area is
, the area is 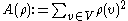 , and the length of a path is the sum of
, and the length of a path is the sum of  over the vertices visited by the path, with multiplicity.
over the vertices visited by the path, with multiplicity.

