
Q-exponential distribution
Encyclopedia
In q-analog
theory, the q-exponential distribution is a probability distribution arising from the maximization of the Tsallis entropy
under appropriate constraints, including constraining the domain to be positive. It is one example of a Tsallis distribution
. The q-exponential is a generalization of the exponential distribution in the same way that Tsallis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon Entropy. The exponential distribution
is recovered as .
.
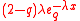
where
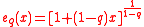
is the q-exponential.
can be derived using the standard Boltzmann–Gibbs entropy or Shannon entropy and constraining the domain of the variable to be positive, the q-exponential distribution can be derived from a maximization of the Tsallis Entropy subject to the appropriate constraints.
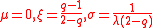
The q-exponential is the generalization of the Lomax distribution (Pareto Type II), as it extends this distribution to the cases of finite support. The Lomax parameters are:
As the Lomax distribution is a shifted version of the Pareto distribution, the q-exponential is a shifted reparameterized generalization of the Pareto. When q > 1, the q-exponential is equivalent to the Pareto shifted to have support starting at zero. Specifically: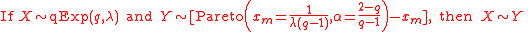
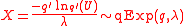
 is the q-logarithm and
is the q-logarithm and 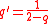
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
theory, the q-exponential distribution is a probability distribution arising from the maximization of the Tsallis entropy
Tsallis entropy
In physics, the Tsallis entropy is a generalization of the standard Boltzmann-Gibbs entropy. In the scientific literature, the physical relevance of the Tsallis entropy is highly debated...
under appropriate constraints, including constraining the domain to be positive. It is one example of a Tsallis distribution
Tsallis distribution
In q-analog theory and statistical mechanics, a Tsallis distribution is a probability distribution derived from the maximization of the Tsallis entropy under appropriate constraints. There are several different families of Tsallis distributions, yet different sources may reference an individual...
. The q-exponential is a generalization of the exponential distribution in the same way that Tsallis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon Entropy. The exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
is recovered as
 .
.Probability density function
The q-exponential distribution has the probability density function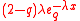
where
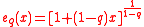
is the q-exponential.
Derivation
In a similar procedure to how the exponential distributionExponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
can be derived using the standard Boltzmann–Gibbs entropy or Shannon entropy and constraining the domain of the variable to be positive, the q-exponential distribution can be derived from a maximization of the Tsallis Entropy subject to the appropriate constraints.
Relationship to other distributions
The q-exponential is a special case of the Generalized Pareto distribution where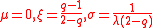
The q-exponential is the generalization of the Lomax distribution (Pareto Type II), as it extends this distribution to the cases of finite support. The Lomax parameters are:

As the Lomax distribution is a shifted version of the Pareto distribution, the q-exponential is a shifted reparameterized generalization of the Pareto. When q > 1, the q-exponential is equivalent to the Pareto shifted to have support starting at zero. Specifically:
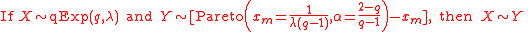
Generating random deviates
Random deviates can be drawn using Inverse transform sampling. Given a variable U that is uniformly distributed on the interval (0,1), then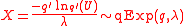
 is the q-logarithm and
is the q-logarithm and 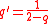
Economics (econophysics)
The q-exponential distribution has been used to describe the distribution of wealth (assets) between individuals.See also
- Constantino TsallisConstantino TsallisConstantino Tsallis is a naturalized Brazilian physicist working in Rio de Janeiro at CBPF, Brazil. He was born in Greece, and grew up in Argentina, where he studied physics at Instituto Balseiro, in Bariloche. In 1974 he received a Doctorat d'Etat et Sciences Physiques degree from the University...
- Tsallis statisticsTsallis statisticsThe term Tsallis statistics usually refers to the collection of q-analogs of mathematical functions and associated probability distributions that were originated by Constantino Tsallis. Using these tools, it is possible to derive Tsallis distributions from the optimization of the Tsallis entropic...
- Tsallis entropyTsallis entropyIn physics, the Tsallis entropy is a generalization of the standard Boltzmann-Gibbs entropy. In the scientific literature, the physical relevance of the Tsallis entropy is highly debated...
- Tsallis distributionTsallis distributionIn q-analog theory and statistical mechanics, a Tsallis distribution is a probability distribution derived from the maximization of the Tsallis entropy under appropriate constraints. There are several different families of Tsallis distributions, yet different sources may reference an individual...
- q-Gaussian
Further reading
- Juniper, J. (2007) "The Tsallis Distribution and Generalised Entropy: Prospects for Future Research into Decision-Making under Uncertainty", Centre of Full Employment and Equity, The University of Newcastle, Australia

