Tsallis entropy
Encyclopedia
In physics, the Tsallis entropy is a generalization of the standard Boltzmann-Gibbs entropy. In the scientific literature, the physical relevance of the Tsallis entropy is highly debated. It is not clear if any system obeys, and if so in which regime, the statistical mechanics that can be derived from such an approach.
The Tsallis entropy is defined as
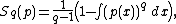
or in the discrete case
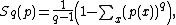
where S denotes entropy, p the probability distribution
of interest, and q is a real parameter. In the limit as q → 1, the normal Boltzmann-Gibbs entropy is recovered.
The parameter q is a measure of the non-extensitivity of the system of interest. There are continuous and discrete versions of this entropic measure.
The Tsallis Entropy has been used along with the Principle of maximum entropy
to derive the Tsallis distribution
.
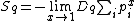
where Dq is the q-derivative
with respect to x. This may be compared to the standard entropy formula:
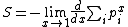
satisfies
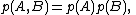
the Tsallis entropy of this system satisfies
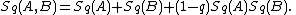
From this result, it is evident that the parameter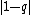
is a measure of the departure from additivity. In the limit when q = 1,
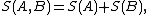
which is what is expected for an additive system. This property is sometimes referred to as "pseudo-additivity".
Tsallis entropy for an exponential family can be written (Nielsen, Nock, 2011) as
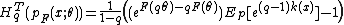
where F is log-normalizer and k the term indicating the carrier measure.
For multivariate normal, term k is zero, and therefore the Tsallis entropy is in closed-form.
The Tsallis entropy is defined as
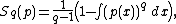
or in the discrete case
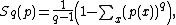
where S denotes entropy, p the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of interest, and q is a real parameter. In the limit as q → 1, the normal Boltzmann-Gibbs entropy is recovered.
The parameter q is a measure of the non-extensitivity of the system of interest. There are continuous and discrete versions of this entropic measure.
The Tsallis Entropy has been used along with the Principle of maximum entropy
Principle of maximum entropy
In Bayesian probability, the principle of maximum entropy is a postulate which states that, subject to known constraints , the probability distribution which best represents the current state of knowledge is the one with largest entropy.Let some testable information about a probability distribution...
to derive the Tsallis distribution
Tsallis distribution
In q-analog theory and statistical mechanics, a Tsallis distribution is a probability distribution derived from the maximization of the Tsallis entropy under appropriate constraints. There are several different families of Tsallis distributions, yet different sources may reference an individual...
.
Various relationships
The discrete Tsallis entropy satisfies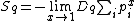where Dq is the q-derivative
Q-derivative
In mathematics, in the area of combinatorics, the q-derivative, or Jackson derivative, is a q-analog of the ordinary derivative, introduced by Frank Hilton Jackson. It is the inverse of Jackson's q-integration-Definition:...
with respect to x. This may be compared to the standard entropy formula:
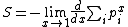
Non-additivity
Given two independent systems A and B, for which the joint probability densityProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
satisfies
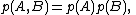
the Tsallis entropy of this system satisfies
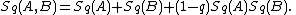
From this result, it is evident that the parameter
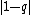is a measure of the departure from additivity. In the limit when q = 1,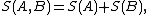which is what is expected for an additive system. This property is sometimes referred to as "pseudo-additivity".
Exponential families
Many common distributions like the normal distribution belongs to the statistical exponential families.Tsallis entropy for an exponential family can be written (Nielsen, Nock, 2011) as
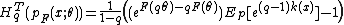
where F is log-normalizer and k the term indicating the carrier measure.
For multivariate normal, term k is zero, and therefore the Tsallis entropy is in closed-form.