Profunctor
Encyclopedia
In category theory
, a branch of mathematics
, profunctors are a generalization of relations
and also of bimodule
s. They are related to the notion of correspondence
s.
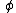from a category
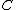to a category 
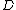, written
,
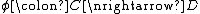is defined to be a functor
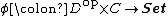
where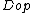
denotes the opposite category
of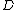
and 
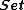denotes the category of sets
. Given morphisms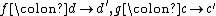
respectively in 
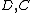and an element 
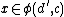, we write 
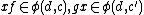to denote the actions.
Using the cartesian closure
of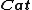
, the category of small categories
, the profunctor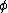
can be seen as a functor
where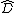
denotes the category 
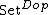of presheaves over 
.
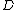A correspondence
from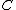
to 
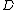is a profunctor 
.
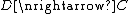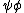of two profunctors
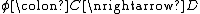and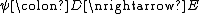 
is given by
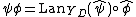
where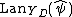
is the left Kan extension
of the functor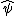
along the Yoneda functor 
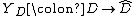of 
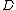(which to every object 
of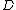 
associates the functor 
).
It can be shown that
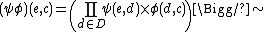
where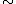
is the least equivalence relation such that 
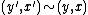whenever there exists a morphism 
in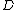 
such that
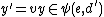and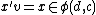 
.
Prof whose
can be seen as a profunctor 
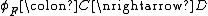by postcomposing with the Yoneda functor:
.
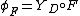It can be shown that such a profunctor
has a right adjoint. Moreover, this is a characterization: a profunctor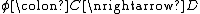 
has a right adjoint if and only if 
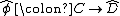factors through the Cauchy completion
of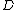
, i.e. there exists a functor 
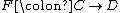such that 
.
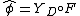Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, profunctors are a generalization of relations
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
and also of bimodule
Bimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
s. They are related to the notion of correspondence
Correspondence (mathematics)
In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...
s.
Definition
A profunctor (also named distributor by the French school and module by the Sydney school)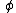 from a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
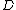to a category , written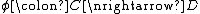,is defined to be a functor
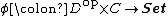
where
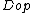denotes the opposite categoryOpposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
of
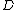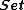and denotes the category of setsCategory of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. Given morphisms
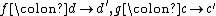respectively in 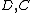and an element 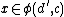, we write 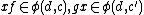to denote the actions.Using the cartesian closure
Cartesian closed category
In category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
of
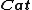, the category of small categoriesCategory of small categories
In mathematics, specifically in category theory, the category of small categories, denoted by Cat, is the category whose objects are all small categories and whose morphisms are functors between categories...
, the profunctor
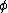can be seen as a functorwhere
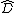denotes the category 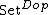of presheaves over 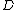.A correspondence
Correspondence (mathematics)
In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...
from
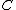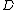to is a profunctor 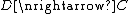.Composition of profunctors
The composite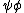 of two profunctors 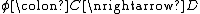and 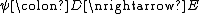is given by
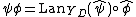
where
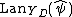is the left Kan extensionKan extension
Kan extensions are universal constructs in category theory, a branch of mathematics. They are closely related to adjoints, but are also related to limits and ends. They are named after Daniel M...
of the functor
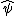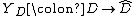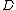along the Yoneda functor of (which to every object of 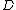associates the functor ).It can be shown that
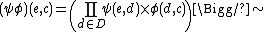
where
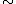is the least equivalence relation such that 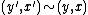whenever there exists a morphism in 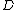such that 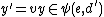and 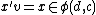.The bicategory of profunctors
Composition of profunctors is associative only up to isomorphism (because the product is not strictly associative in Set). The best one can hope is therefore to build a bicategoryBicategory
In mathematics, a bicategory is a concept in category theory used to extend the notion of category to handle the cases where the composition of morphisms is not associative, but only associative up to an isomorphism. The notion was introduced in 1967 by Jean Bénabou.Formally, a bicategory B...
Prof whose
- 0-cells are small categories,
- 1-cells between two small categories are the profunctors between those categories,
- 2-cells between two profunctors are the natural transformationNatural transformationIn category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s between those profunctors.
Lifting functors to profunctors
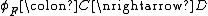A functor can be seen as a profunctor by postcomposing with the Yoneda functor: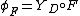.It can be shown that such a profunctor
has a right adjoint. Moreover, this is a characterization: a profunctor 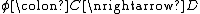has a right adjoint if and only if 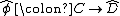factors through the Cauchy completionKaroubi envelope
In mathematics the Karoubi envelope of a category C is a classification of the idempotents of C, by means of an auxiliary category. Taking the Karoubi envelope of a preadditive category gives a pseudo-abelian category, hence the construction is sometimes called the pseudo-abelian completion...
of
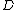, i.e. there exists a functor 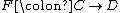such that .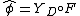