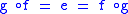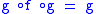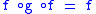Karoubi envelope
Encyclopedia
In mathematics
the Karoubi envelope (or Cauchy completion or idempotent splitting) of a category
C is a classification of the idempotents of C, by means of an auxiliary category. Taking the Karoubi envelope of a preadditive category
gives a pseudo-abelian category
, hence the construction is sometimes called the pseudo-abelian completion. It is named for the French mathematician Max Karoubi
.
Given a category C, an idempotent of C is an endomorphism

with
 .
.
An idempotent e: A → A is said to split if there is an object B and morphisms f: A → B,
g : B → A such that e = g f and 1B = f g.
The Karoubi envelope of C, sometimes written Split(C), is the category whose objects are pairs of the form (A, e) where A is an object of C and is an idempotent of C, and whose morphism
is an idempotent of C, and whose morphism
s are triples of the form
where is a morphism of C satisfying
is a morphism of C satisfying 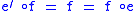 (or equivalently
(or equivalently 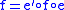 ).
).
Composition in Split(C) is as in C, but the identity morphism
on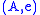 in Split(C) is
in Split(C) is 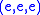 , rather than
, rather than
the identity on .
.
The category C embeds fully and faithfully in Split(C). In Split(C) every idempotent splits, and Split(C) is the universal category with this property.
The Karoubi envelope of a category C can therefore be considered as the "completion" of C which splits idempotents.
The Karoubi envelope of a category C can equivalently be defined as the full subcategory of (the presheaves over C) of retracts of representable functor
(the presheaves over C) of retracts of representable functor
s. The category of presheaves on C is equivalent to the category of presheaves on Split(C).
in Split(C) is of the form , with inverse
, with inverse 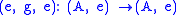 satisfying:
satisfying:
If the first equation is relaxed to just have , then f is a partial automorphism (with inverse g). A (partial) involution in Split(C) is a self-inverse (partial) automorphism.
, then f is a partial automorphism (with inverse g). A (partial) involution in Split(C) is a self-inverse (partial) automorphism.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Karoubi envelope (or Cauchy completion or idempotent splitting) of a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
C is a classification of the idempotents of C, by means of an auxiliary category. Taking the Karoubi envelope of a preadditive category
Preadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
gives a pseudo-abelian category
Pseudo-abelian category
In mathematics, specifically in category theory, a pseudo-abelian category is a category that is preadditive and is such that every idempotent has a kernel...
, hence the construction is sometimes called the pseudo-abelian completion. It is named for the French mathematician Max Karoubi
Max Karoubi
Max Karoubi is French a mathematician who works on K-theory and who founded the European mathematical society. He was one of Henri Cartan's students.-References:* of Max Karoubi* in nlab...
.
Given a category C, an idempotent of C is an endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...

with
 .
.An idempotent e: A → A is said to split if there is an object B and morphisms f: A → B,
g : B → A such that e = g f and 1B = f g.
The Karoubi envelope of C, sometimes written Split(C), is the category whose objects are pairs of the form (A, e) where A is an object of C and
 is an idempotent of C, and whose morphism
is an idempotent of C, and whose morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s are triples of the form
where
 is a morphism of C satisfying
is a morphism of C satisfying 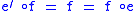 (or equivalently
(or equivalently 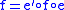 ).
).Composition in Split(C) is as in C, but the identity morphism
on
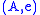 in Split(C) is
in Split(C) is 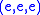 , rather than
, rather thanthe identity on
 .
.The category C embeds fully and faithfully in Split(C). In Split(C) every idempotent splits, and Split(C) is the universal category with this property.
The Karoubi envelope of a category C can therefore be considered as the "completion" of C which splits idempotents.
The Karoubi envelope of a category C can equivalently be defined as the full subcategory of
 (the presheaves over C) of retracts of representable functor
(the presheaves over C) of retracts of representable functorRepresentable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
s. The category of presheaves on C is equivalent to the category of presheaves on Split(C).
Automorphisms in the Karoubi envelope
An automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
in Split(C) is of the form
 , with inverse
, with inverse 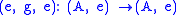 satisfying:
satisfying:If the first equation is relaxed to just have
 , then f is a partial automorphism (with inverse g). A (partial) involution in Split(C) is a self-inverse (partial) automorphism.
, then f is a partial automorphism (with inverse g). A (partial) involution in Split(C) is a self-inverse (partial) automorphism.Examples
- If C has products, then given an isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
 the mapping
the mapping  , composed with the canonical map
, composed with the canonical map  of symmetry, is a partial involution.
of symmetry, is a partial involution. - If C is a triangulated categoryTriangulated categoryA triangulated category is a mathematical category satisfying some axioms that are based on the properties of the homotopy category of spectra, and the derived category of an abelian category. A t-category is a triangulated category with a t-structure.- History :The notion of a derived category...
, the Karoubi envelope Split(C) can be endowed with the structure of a triangulated category such that the canonical functor C → Split(C) becomes a triangulated functor. - The Karoubi envelope is used in the construction of several categories of motivesMotive (algebraic geometry)In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
. - The Karoubi envelope construction takes semi-adjunctions to adjunctions. For this reason the Karoubi envelope is used in the study of models of the untyped lambda calculus. The Karoubi envelope of an extensional lambda model (a monoid, considered as a category) is cartesian closed.