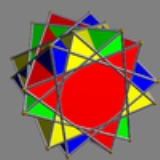
Prismatic compound of antiprisms with rotational freedom
Encyclopedia
| Compound of 2n p/q-gonal antiprisms | |||
|---|---|---|---|
|
|||
| Type | Uniform compound Uniform polyhedron compound A uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.The uniform polyhedron compounds were first enumerated by John Skilling... |
||
| Index |
|
||
| Polyhedra | 2n p/q-gonal antiprisms Prismatic uniform polyhedron In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms... |
||
| Faces | 4n {p/q} (unless p/q=2), 4np triangles | ||
| Edges | 8np | ||
| Vertices | 4np | ||
| Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:... (Dnpd) Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:... (Dnph) |
||
| Subgroup Subgroup In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H... restricting to one constituent |
Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry... (S2p) Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry... (Cph) |
||
Each member of this infinite family of uniform polyhedron compound
Uniform polyhedron compound
A uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.The uniform polyhedron compounds were first enumerated by John Skilling...
s is a symmetric arrangement of antiprisms
Prismatic uniform polyhedron
In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms...
sharing a common axis of rotational symmetry. It arises from superimposing two copies of the corresponding prismatic compound of antiprisms
Prismatic compound of antiprisms
Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of antiprisms sharing a common axis of rotational symmetry.This infinite family can be enumerated as follows:...
(without rotational freedom), and rotating each copy by an equal and opposite angle.
This infinite family can be enumerated as follows:
- For each positive integer n>0 and for each rational number p/q>3/2 (expressed with p and q coprimeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
), there occurs the compound of 2n p/q-gonal antiprisms (with rotational freedom), with symmetry group:- Dnpd if nq is odd
- Dnph if nq is even
Where p/q=2 the component is a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, sometimes not considered a true antiprism.


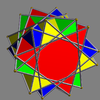 (n=2, p=3, q=1)
(n=2, p=3, q=1) (n=1, p=7, q=2)
(n=1, p=7, q=2)