János Pintz
Encyclopedia
János Pintz is a Hungarian
mathematician
working in analytic number theory
. He is a fellow of the Rényi Mathematical Institute
and is also a member of the Hungarian Academy of Sciences
.
where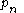
denotes the nth prime number
. In other words, for every c > 0, there exist infinitely many pairs of consecutive primes pn and pn+1 that are closer to each other than the average distance between consecutive primes by a factor of c, i.e., pn+1 − pn < c log pn.
This result was originally reported in 2003 by Dan Goldston and Cem Yıldırım but was later retracted. Then Janos Pintz joined the team and completed the proof in 2005. Later they improved this to showing that pn+1-pn<c√log n(log log n)2 occurs infinitely often.
Further, if one assumes the Elliott-Halberstam conjecture
, then one can also show that primes within 16 of each other occur infinitely often, which is nearly the twin prime conjecture
.
Hungary
Hungary , officially the Republic of Hungary , is a landlocked country in Central Europe. It is situated in the Carpathian Basin and is bordered by Slovakia to the north, Ukraine and Romania to the east, Serbia and Croatia to the south, Slovenia to the southwest and Austria to the west. The...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
working in analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
. He is a fellow of the Rényi Mathematical Institute
Alfréd Rényi Institute of Mathematics
The Alfréd Rényi Institute of Mathematics is the research institute in mathematics of the Hungarian Academy of Sciences. It was created in 1950 by Alfréd Rényi, who directed it until his death. Since its creation, the institute has been the center of mathematical research in Hungary. It received...
and is also a member of the Hungarian Academy of Sciences
Hungarian Academy of Sciences
The Hungarian Academy of Sciences is the most important and prestigious learned society of Hungary. Its seat is at the bank of the Danube in Budapest.-History:...
.
Mathematical results
- With János KomlósJános Komlós (mathematician)János Komlós is a Hungarian-American mathematician, working in probability theory and discrete mathematics. He is a professor of mathematics at Rutgers University since 1988. He graduated from the Eötvös Loránd University, then became a fellow at the Mathematical Institute of the Hungarian Academy...
and Endre SzemerédiEndre SzemerédiEndre Szemerédi is a Hungarian mathematician, working in the field of combinatorics and theoretical computer science. He is the State of New Jersey Professor of computer science at Rutgers University since 1986...
disproved the Heilbronn conjectureHeilbronn triangle problemIn mathematics, the Heilbronn triangle problem is a typical question in the area of irregularities of distribution, within elementary geometry....
. - With IwaniecHenryk IwaniecHenryk Iwaniec is a Polish American mathematician, and since 1987 a professor at Rutgers University. He was awarded the fourteenth Frank Nelson Cole Prize in Number Theory in 2002. He received the Leroy P. Steele Prize for Mathematical Exposition in 2011.-Background and education:Iwaniec studied...
he proved that for sufficiently large n there is a prime between n and n+n23/42. - Pintz gave an effective upper bound for the first number for which the Mertens conjectureMertens conjectureIn mathematics, the Mertens conjecture is the incorrect statement that the Mertens function M is bounded by √n, which implies the Riemann hypothesis...
fails. - He gave a O(x2/3) upper bound for the number of those numbers that are less than x and not the sum of two primes.
- With Imre Z. RuzsaImre Z. RuzsaImre Z. Ruzsa is a Hungarian mathematician specializing in number theory.Ruzsa participated in the International Mathematical Olympiad for Hungary, winning a silver medal in 1969, and two consecutive gold medals with perfect scores in 1970 and 1971. He graduated from the Eötvös Loránd University...
he improved a result of LinnikYuri LinnikYuri Vladimirovich Linnik was a Soviet mathematician active in number theory, probability theory and mathematical statistics.Linnik was born in Bila Tserkva, in present-day Ukraine. He went to St Petersburg University where his supervisor was Vladimir Tartakovski, and later worked at that...
by showing that every sufficiently large even number is the sum of two primes and at most 8 powers of 2. - Pintz is best known for the following result that he, Daniel GoldstonDaniel GoldstonDaniel Alan Goldston is an American mathematician who specializes in number theory. He is currently a professor of mathematics at San Jose State University....
, and Cem YıldırımCem YildirimCem Yalçın Yıldırım is a Turkish mathematician who specializes in number theory. He obtained his PhD from the University of Toronto in 1990. His advisor was John Friedlander...
proved in 2005: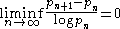
where
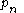denotes the nth prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. In other words, for every c > 0, there exist infinitely many pairs of consecutive primes pn and pn+1 that are closer to each other than the average distance between consecutive primes by a factor of c, i.e., pn+1 − pn < c log pn.
This result was originally reported in 2003 by Dan Goldston and Cem Yıldırım but was later retracted. Then Janos Pintz joined the team and completed the proof in 2005. Later they improved this to showing that pn+1-pn<c√log n(log log n)2 occurs infinitely often.
Further, if one assumes the Elliott-Halberstam conjecture
Elliott-Halberstam conjecture
In number theory, the Elliott–Halberstam conjecture is a conjecture about the distribution of prime numbers in arithmetic progressions. It has many applications in sieve theory. It is named for Peter D. T. A. Elliott and Heini Halberstam....
, then one can also show that primes within 16 of each other occur infinitely often, which is nearly the twin prime conjecture
Twin prime
A twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
.
- Goldston, S. W. Graham, Pintz, and Yıldırım proved that the difference between numbers which are products of exactly 2 primes is infinitely often at most 6.
See also
- Twin prime conjectureTwin primeA twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
- Mertens conjectureMertens conjectureIn mathematics, the Mertens conjecture is the incorrect statement that the Mertens function M is bounded by √n, which implies the Riemann hypothesis...
- Heilbronn triangle problemHeilbronn triangle problemIn mathematics, the Heilbronn triangle problem is a typical question in the area of irregularities of distribution, within elementary geometry....
- Prime gap
- Landau's problemsLandau's problemsAt the 1912 International Congress of Mathematicians, Edmund Landau listed four basic problems about primes. These problems were characterised in his speech as "unattackable at the present state of science" and are now known as Landau's problems...
- Fazekas Mihály Gimnázium
- Maier's theoremMaier's theoremIn number theory, Maier's theorem is a theorem about the numbers of primes in short intervals for which the Cramér's probabilistic model of primes gives the wrong answer.It states that if π is the prime counting function and λ is greater than 1 then...
External links
- János Pintz's page at the Alfréd Rényi Institute of MathematicsAlfréd Rényi Institute of MathematicsThe Alfréd Rényi Institute of Mathematics is the research institute in mathematics of the Hungarian Academy of Sciences. It was created in 1950 by Alfréd Rényi, who directed it until his death. Since its creation, the institute has been the center of mathematical research in Hungary. It received...