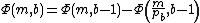
Prime counting function
Encyclopedia
In mathematics
, the prime-counting function is the function
counting the number of prime number
s less than or equal to some real number
x. It is denoted by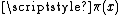 (this does not refer to the number π
(this does not refer to the number π
).
is the growth rate
of the prime-counting function. It was conjecture
d in the end of the 18th century by Gauss
and by Legendre
to be approximately
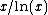
in the sense that

This statement is the prime number theorem
. An equivalent statement is
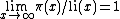
where li is the logarithmic integral function. The prime number theorem was first proved in 1896 by Jacques Hadamard
and by Charles de la Vallée Poussin
independently, using properties of the Riemann zeta function introduced by Riemann
in 1859.
More precise estimates of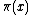 are now known; for example
are now known; for example
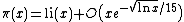
where the O is big O notation
. For a most values of we are interested in (i.e., when
we are interested in (i.e., when  is not unreasonably large)
is not unreasonably large) 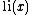 is greater than
is greater than 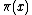 , but infinitely often the opposite is true. For a discussion of this, see Skewes' number.
, but infinitely often the opposite is true. For a discussion of this, see Skewes' number.
Proofs of the prime number theorem not using the zeta function or complex analysis
were found around 1948 by Atle Selberg
and by Paul Erdős
(for the most part independently).
In the On-Line Encyclopedia of Integer Sequences
, the π(x) column is sequence , π(x) - x / ln x is sequence , and li(x) − π(x) is sequence . The value for π(1024) is by J. Buethe, J. Franke
, A. Jost, and T. Kleinjung and assumes the Riemann hypothesis
.
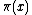 , if
, if  is not too large, is to use the sieve of Eratosthenes
is not too large, is to use the sieve of Eratosthenes
to produce the primes less than or equal to and then to count them.
and then to count them.
A more elaborate way of finding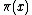 is due to Legendre
is due to Legendre
: given , if
, if 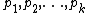 are distinct prime numbers, then the number of integers less than or equal to
are distinct prime numbers, then the number of integers less than or equal to  which are divisible by no
which are divisible by no  is
is
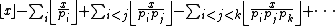
(where denotes the floor function
denotes the floor function
). This number is therefore equal to
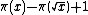
when the numbers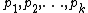 are the prime numbers less than or equal to the square root of
are the prime numbers less than or equal to the square root of  .
.
In a series of articles published between 1870 and 1885, Ernst Meissel
described (and used) a practical combinatorial way of evaluating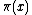 . Let
. Let  ,
, 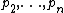 be the first
be the first  primes and denote by
primes and denote by 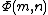 the number of natural numbers not greater than
the number of natural numbers not greater than  which are divisible by no
which are divisible by no  . Then
. Then
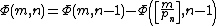
Given a natural number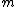 , if
, if 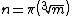 and if
and if 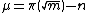 , then
, then

Using this approach, Meissel computed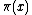 , for
, for  equal to 5×105, 106, 107, and 108.
equal to 5×105, 106, 107, and 108.
In 1959, Derrick Henry Lehmer
extended and simplified Meissel's method. Define, for real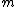 and for natural numbers
and for natural numbers  , and
, and 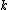 ,
, 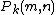 as the number of numbers not greater than m with exactly k prime factors, all greater than
as the number of numbers not greater than m with exactly k prime factors, all greater than  . Furthermore, set
. Furthermore, set 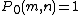 . Then
. Then
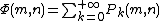
where the sum actually has only finitely many nonzero terms. Let denote an integer such that
denote an integer such that 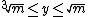 , and set
, and set  . Then
. Then 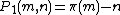 and
and 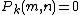 when
when 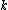 ≥ 3. Therefore
≥ 3. Therefore

The computation of can be obtained this way:
can be obtained this way:
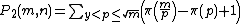
On the other hand, the computation of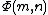 can be done using the following rules:
can be done using the following rules:
Using his method and an IBM
701, Lehmer was able to compute .
.
Further improvements to this method were made by Lagarias, Miller, Odlyzko, Deléglise and Rivat.
The Chinese mathematician
Hwang Cheng, in a conference about prime number functions at the University of Bordeaux
, used the following identities:
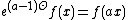

and setting , Laplace-transforming both sides and applying a geometric sum on
, Laplace-transforming both sides and applying a geometric sum on 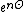 got the expression
got the expression
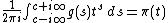
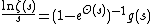
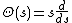
 or
or 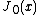 . This has jumps of 1/n for prime powers pn, with it taking a value half-way between the two sides at discontinuities. That added detail is because then it may be defined by an inverse Mellin transform
. This has jumps of 1/n for prime powers pn, with it taking a value half-way between the two sides at discontinuities. That added detail is because then it may be defined by an inverse Mellin transform
. Formally, we may define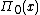 by
by
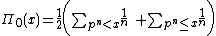
where p is a prime.
We may also write
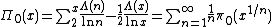
where Λ(n) is the von Mangoldt function
and

Möbius inversion formula
then gives
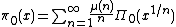
Knowing the relationship between log of the Riemann zeta function and the von Mangoldt function
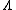 , and using the Perron formula we have
, and using the Perron formula we have
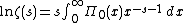
The Chebyshev function
weights primes or prime powers pn by ln(p):
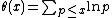
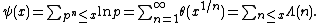
Riemann's prime-counting function has the ordinary generating function:
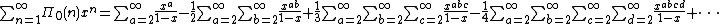
. They stem from the work of Riemann and von Mangoldt
, and are generally known as explicit formulas.
We have the following expression for ψ:
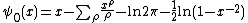
where
Here ρ are the zeros of the Riemann zeta function in the critical strip, where the real part of ρ is between zero and one. The formula is valid for values of x greater than one, which is the region of interest. The sum over the roots is conditionally convergent, and should be taken in order of increasing absolute value of the imaginary part. Note that the same sum over the trivial roots gives the last subtrahend in the formula.
For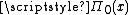 we have a more complicated formula
we have a more complicated formula
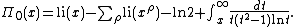
Again, the formula is valid for x > 1, while ρ are the nontrivial zeros of the zeta function ordered according to their absolute value, and, again, the latter integral, taken with minus sign, is just the same sum, but over the trivial zeros. The first term li(x) is the usual logarithmic integral function
; the expression li(xρ) in the second term should be considered as Ei(ρ ln x), where Ei is the analytic continuation
of the exponential integral
function from positive reals to the complex plane with branch cut along the negative reals.
Thus, Möbius inversion formula
gives us
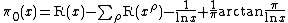
valid for x > 1, where
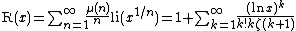
is so-called Riemann's R-function. The latter series for it is known as Gram series and converges for all positive x.
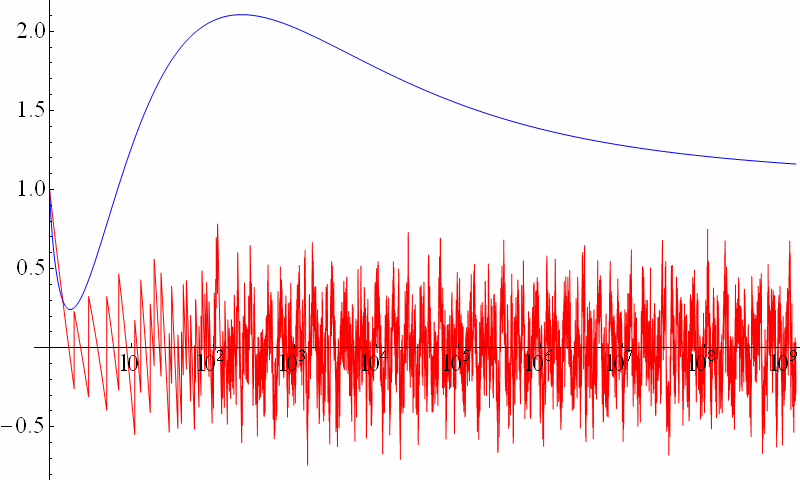 The sum over non-trivial zeta zeros in the formula for
The sum over non-trivial zeta zeros in the formula for 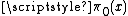 describes the fluctuations of
describes the fluctuations of  , while the remaining terms give the "smooth" part of prime-counting function, so one can use
, while the remaining terms give the "smooth" part of prime-counting function, so one can use
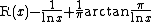
as the best estimator of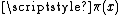 for x > 1.
for x > 1.
The amplitude of the "noisy" part is heuristically about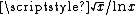 , so the fluctuations of the distribution of primes may be clearly represented with the Δ-function:
, so the fluctuations of the distribution of primes may be clearly represented with the Δ-function:
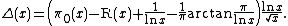
An extensive table of the values of Δ(x) is available.
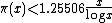 for x > 1.
for x > 1.
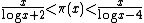 for x ≥ 55.
for x ≥ 55.
Here are some inequalities for the nth prime, pn.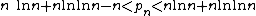 for n ≥ 6.
for n ≥ 6.
The left inequality holds for n ≥ 1 and the right inequality holds for n ≥ 6.
An approximation for the nth prime number is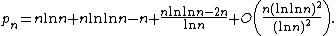
is equivalent to a much tighter bound on the error in the estimate for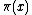 , and hence to a more regular distribution of prime numbers,
, and hence to a more regular distribution of prime numbers,
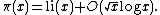
Specifically,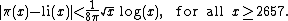
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the prime-counting function is the function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
counting the number of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s less than or equal to some real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
x. It is denoted by
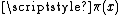 (this does not refer to the number π
(this does not refer to the number πPi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
).
History
Of great interest in number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
is the growth rate
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
of the prime-counting function. It was conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
d in the end of the 18th century by Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
and by Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
to be approximately
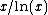
in the sense that

This statement is the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
. An equivalent statement is
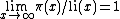
where li is the logarithmic integral function. The prime number theorem was first proved in 1896 by Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
and by Charles de la Vallée Poussin
Charles Jean de la Vallée-Poussin
Charles-Jean Étienne Gustave Nicolas de la Vallée Poussin was a Belgian mathematician. He is most well known for proving the Prime number theorem.The king of Belgium ennobled him with the title of baron.-Biography:...
independently, using properties of the Riemann zeta function introduced by Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
in 1859.
More precise estimates of
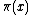 are now known; for example
are now known; for example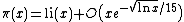
where the O is big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
. For a most values of
 we are interested in (i.e., when
we are interested in (i.e., when  is not unreasonably large)
is not unreasonably large) 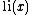 is greater than
is greater than 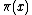 , but infinitely often the opposite is true. For a discussion of this, see Skewes' number.
, but infinitely often the opposite is true. For a discussion of this, see Skewes' number.Proofs of the prime number theorem not using the zeta function or complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
were found around 1948 by Atle Selberg
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
and by Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
(for the most part independently).
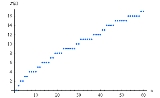
Table of π(x), x / ln x, and li(x)
The table shows how the three functions π(x), x / ln x and li(x) compare at powers of 10. See also, and.| x | π(x) | π(x) − x / ln x | li(x) − π(x) | x / π(x) |
|---|---|---|---|---|
| 10 | 4 | −0.3 | 2.2 | 2.500 |
| 102 | 25 | 3.3 | 5.1 | 4.000 |
| 103 | 168 | 23 | 10 | 5.952 |
| 104 | 1,229 | 143 | 17 | 8.137 |
| 105 | 9,592 | 906 | 38 | 10.425 |
| 106 | 78,498 | 6,116 | 130 | 12.740 |
| 107 | 664,579 | 44,158 | 339 | 15.047 |
| 108 | 5,761,455 | 332,774 | 754 | 17.357 |
| 109 | 50,847,534 | 2,592,592 | 1,701 | 19.667 |
| 1010 | 455,052,511 | 20,758,029 | 3,104 | 21.975 |
| 1011 | 4,118,054,813 | 169,923,159 | 11,588 | 24.283 |
| 1012 | 37,607,912,018 | 1,416,705,193 | 38,263 | 26.590 |
| 1013 | 346,065,536,839 | 11,992,858,452 | 108,971 | 28.896 |
| 1014 | 3,204,941,750,802 | 102,838,308,636 | 314,890 | 31.202 |
| 1015 | 29,844,570,422,669 | 891,604,962,452 | 1,052,619 | 33.507 |
| 1016 | 279,238,341,033,925 | 7,804,289,844,393 | 3,214,632 | 35.812 |
| 1017 | 2,623,557,157,654,233 | 68,883,734,693,281 | 7,956,589 | 38.116 |
| 1018 | 24,739,954,287,740,860 | 612,483,070,893,536 | 21,949,555 | 40.420 |
| 1019 | 234,057,667,276,344,607 | 5,481,624,169,369,960 | 99,877,775 | 42.725 |
| 1020 | 2,220,819,602,560,918,840 | 49,347,193,044,659,701 | 222,744,644 | 45.028 |
| 1021 | 21,127,269,486,018,731,928 | 446,579,871,578,168,707 | 597,394,254 | 47.332 |
| 1022 | 201,467,286,689,315,906,290 | 4,060,704,006,019,620,994 | 1,932,355,208 | 49.636 |
| 1023 | 1,925,320,391,606,803,968,923 | 37,083,513,766,578,631,309 | 7,250,186,216 | 51.939 |
| 1024 | 18,435,599,767,349,200,867,866 | 339,996,354,713,708,049,069 | 17,146,907,278 | 54.243 |
In the On-Line Encyclopedia of Integer Sequences
On-Line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...
, the π(x) column is sequence , π(x) - x / ln x is sequence , and li(x) − π(x) is sequence . The value for π(1024) is by J. Buethe, J. Franke
Jens Franke
Jens Franke is a German mathematician. He holds a chair at the University of Bonn's Hausdorff Center for Mathematics since 1992. Franke's research has covered various problems of number theory, algebraic geometry and analysis on locally symmetric spaces.Franke attended the University of Jena,...
, A. Jost, and T. Kleinjung and assumes the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
.
Algorithms for evaluating π(x)
A simple way to find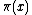 , if
, if  is not too large, is to use the sieve of Eratosthenes
is not too large, is to use the sieve of EratosthenesSieve of Eratosthenes
In mathematics, the sieve of Eratosthenes , one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to a specified integer....
to produce the primes less than or equal to
 and then to count them.
and then to count them.A more elaborate way of finding
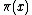 is due to Legendre
is due to LegendreAdrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
: given
 , if
, if 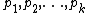 are distinct prime numbers, then the number of integers less than or equal to
are distinct prime numbers, then the number of integers less than or equal to  which are divisible by no
which are divisible by no  is
is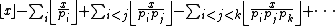
(where
 denotes the floor function
denotes the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
). This number is therefore equal to
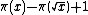
when the numbers
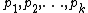 are the prime numbers less than or equal to the square root of
are the prime numbers less than or equal to the square root of  .
.In a series of articles published between 1870 and 1885, Ernst Meissel
Ernst Meissel
Daniel Friedrich Ernst Meissel was a German astronomer who contributed to various aspects of number theory.-External links:...
described (and used) a practical combinatorial way of evaluating
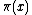 . Let
. Let  ,
, 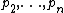 be the first
be the first  primes and denote by
primes and denote by 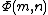 the number of natural numbers not greater than
the number of natural numbers not greater than  which are divisible by no
which are divisible by no  . Then
. Then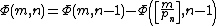
Given a natural number
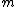 , if
, if 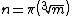 and if
and if 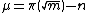 , then
, then
Using this approach, Meissel computed
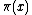 , for
, for  equal to 5×105, 106, 107, and 108.
equal to 5×105, 106, 107, and 108.In 1959, Derrick Henry Lehmer
Derrick Henry Lehmer
Derrick Henry "Dick" Lehmer was an American mathematician who refined Édouard Lucas' work in the 1930s and devised the Lucas–Lehmer test for Mersenne primes...
extended and simplified Meissel's method. Define, for real
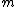 and for natural numbers
and for natural numbers  , and
, and 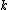 ,
, 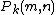 as the number of numbers not greater than m with exactly k prime factors, all greater than
as the number of numbers not greater than m with exactly k prime factors, all greater than  . Furthermore, set
. Furthermore, set 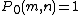 . Then
. Then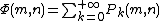
where the sum actually has only finitely many nonzero terms. Let
 denote an integer such that
denote an integer such that 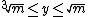 , and set
, and set  . Then
. Then 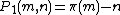 and
and 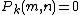 when
when 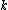 ≥ 3. Therefore
≥ 3. Therefore
The computation of
 can be obtained this way:
can be obtained this way: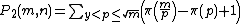
On the other hand, the computation of
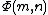 can be done using the following rules:
can be done using the following rules:Using his method and an IBM
IBM
International Business Machines Corporation or IBM is an American multinational technology and consulting corporation headquartered in Armonk, New York, United States. IBM manufactures and sells computer hardware and software, and it offers infrastructure, hosting and consulting services in areas...
701, Lehmer was able to compute
 .
.Further improvements to this method were made by Lagarias, Miller, Odlyzko, Deléglise and Rivat.
The Chinese mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Hwang Cheng, in a conference about prime number functions at the University of Bordeaux
University of Bordeaux
University of Bordeaux is an association of higher education institutions in and around Bordeaux, France. Its current incarnation was established 21 March 2007. The group is the largest system of higher education schools in southwestern France. It is part of the Academy of Bordeaux.There are seven...
, used the following identities:
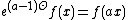

and setting
 , Laplace-transforming both sides and applying a geometric sum on
, Laplace-transforming both sides and applying a geometric sum on 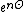 got the expression
got the expression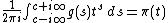
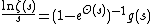
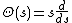
Other prime-counting functions
Other prime-counting functions are also used because they are more convenient to work with. One is Riemann's prime-counting function, usually denoted as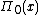 or
or 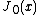 . This has jumps of 1/n for prime powers pn, with it taking a value half-way between the two sides at discontinuities. That added detail is because then it may be defined by an inverse Mellin transform
. This has jumps of 1/n for prime powers pn, with it taking a value half-way between the two sides at discontinuities. That added detail is because then it may be defined by an inverse Mellin transformMellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
. Formally, we may define
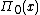 by
by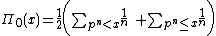
where p is a prime.
We may also write
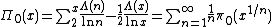
where Λ(n) is the von Mangoldt function
Von Mangoldt function
In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt.-Definition:The von Mangoldt function, conventionally written as Λ, is defined as...
and

Möbius inversion formula
Möbius inversion formula
In mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius. Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by...
then gives
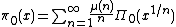
Knowing the relationship between log of the Riemann zeta function and the von Mangoldt function
Von Mangoldt function
In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt.-Definition:The von Mangoldt function, conventionally written as Λ, is defined as...
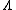 , and using the Perron formula we have
, and using the Perron formula we have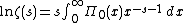
The Chebyshev function
Chebyshev function
[Image:ChebyshevPsi.png|thumb|right|The Chebyshev function ψ, with x [Image:ChebyshevPsi.png|thumb|right|The Chebyshev function ψ, with x ...
weights primes or prime powers pn by ln(p):
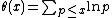
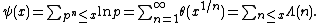
Riemann's prime-counting function has the ordinary generating function:
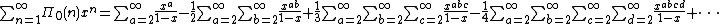
Formulas for prime-counting functions
Formulas for prime-counting functions come in two kinds: arithmetic formulas and analytic formulas. Analytic formulas for prime-counting were the first used to prove the prime number theoremPrime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
. They stem from the work of Riemann and von Mangoldt
Hans Carl Friedrich von Mangoldt
Hans Carl Friedrich von Mangoldt was a German mathematician who contributed to the solution of the prime number theorem.Von Mangoldt completed his Doctor of Philosophy in 1878 at the University of Berlin, where his advisors were Ernst Kummer and Karl Weierstrass...
, and are generally known as explicit formulas.
We have the following expression for ψ:
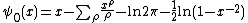
where
Here ρ are the zeros of the Riemann zeta function in the critical strip, where the real part of ρ is between zero and one. The formula is valid for values of x greater than one, which is the region of interest. The sum over the roots is conditionally convergent, and should be taken in order of increasing absolute value of the imaginary part. Note that the same sum over the trivial roots gives the last subtrahend in the formula.
For
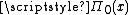 we have a more complicated formula
we have a more complicated formula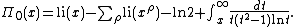
Again, the formula is valid for x > 1, while ρ are the nontrivial zeros of the zeta function ordered according to their absolute value, and, again, the latter integral, taken with minus sign, is just the same sum, but over the trivial zeros. The first term li(x) is the usual logarithmic integral function
Logarithmic integral function
In mathematics, the logarithmic integral function or integral logarithm li is a special function. It occurs in problems of physics and has number theoretic significance, occurring in the prime number theorem as an estimate of the number of prime numbers less than a given value.-Integral...
; the expression li(xρ) in the second term should be considered as Ei(ρ ln x), where Ei is the analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of the exponential integral
Exponential integral
In mathematics, the exponential integral is a special function defined on the complex plane given the symbol Ei.-Definitions:For real, nonzero values of x, the exponential integral Ei can be defined as...
function from positive reals to the complex plane with branch cut along the negative reals.
Thus, Möbius inversion formula
Möbius inversion formula
In mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius. Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by...
gives us
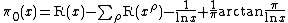
valid for x > 1, where
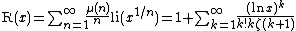
is so-called Riemann's R-function. The latter series for it is known as Gram series and converges for all positive x.

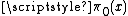 describes the fluctuations of
describes the fluctuations of  , while the remaining terms give the "smooth" part of prime-counting function, so one can use
, while the remaining terms give the "smooth" part of prime-counting function, so one can use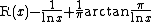
as the best estimator of
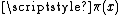 for x > 1.
for x > 1.The amplitude of the "noisy" part is heuristically about
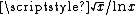 , so the fluctuations of the distribution of primes may be clearly represented with the Δ-function:
, so the fluctuations of the distribution of primes may be clearly represented with the Δ-function: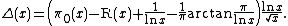
An extensive table of the values of Δ(x) is available.
Inequalities
Here are some useful inequalities for π(x).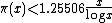 for x > 1.
for x > 1.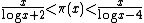 for x ≥ 55.
for x ≥ 55.Here are some inequalities for the nth prime, pn.
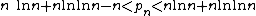 for n ≥ 6.
for n ≥ 6.The left inequality holds for n ≥ 1 and the right inequality holds for n ≥ 6.
An approximation for the nth prime number is
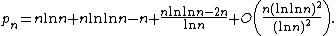
The Riemann hypothesis
The Riemann hypothesisRiemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
is equivalent to a much tighter bound on the error in the estimate for
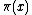 , and hence to a more regular distribution of prime numbers,
, and hence to a more regular distribution of prime numbers,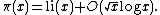
Specifically,
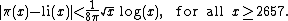
External links
- Chris Caldwell, The Nth Prime Page at The Prime PagesPrime pagesThe Prime Pages is a website about prime numbers maintained by Chris Caldwell at the University of Tennessee at Martin.The site maintains the list of the "5,000 largest known primes", selected smaller primes of special forms, and many "top twenty" lists for primes of various forms...
.