
Prim's algorithm
Encyclopedia
In computer science
, Prim's algorithm is a greedy algorithm
that finds a minimum spanning tree
for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree
that includes every vertex
, where the total weight of all the edges
in the tree is minimized. The algorithm was developed in 1930 by Czech
mathematician Vojtěch Jarník
and later independently by computer scientist
Robert C. Prim
in 1957 and rediscovered by Edsger Dijkstra
in 1959. Therefore it is also sometimes called the DJP algorithm, the Jarník algorithm, or the Prim–Jarník algorithm.
Other algorithms for this problem include Kruskal's algorithm
and Borůvka's algorithm
.
The algorithm continuously increases the size of a tree, one edge at a time, starting with a tree consisting of a single vertex, until it spans all vertices.
A simple implementation using an adjacency matrix
graph representation and searching an array of weights to find the minimum weight edge to add requires O(V2) running time. Using a simple binary heap
data structure and an adjacency list
representation, Prim's algorithm can be shown to run in time O(E log V) where E is the number of edges and V is the number of vertices. Using a more sophisticated Fibonacci heap
, this can be brought down to O(E + V log V), which is asymptotically faster
when the graph is dense
enough that E is Ω(V).
. At every iteration of Prim's algorithm, an edge must be found that connects a vertex in a subgraph to a vertex outside the subgraph. Since P is connected, there will always be a path to every vertex. The output Y of Prim's algorithm is a tree
, because the edge and vertex added to Y are connected. Let Y1 be a minimum spanning tree of P. If Y1=Y then Y is a minimum spanning tree. Otherwise, let e be the first edge added during the construction of Y that is not in Y1, and V be the set of vertices connected by the edges added before e. Then one endpoint of e is in V and the other is not. Since Y1 is a spanning tree of P, there is a path in Y1 joining the two endpoints. As one travels along the path, one must encounter an edge f joining a vertex in V to one that is not in V. Now, at the iteration when e was added to Y, f could also have been added and it would be added instead of e if its weight was less than e. Since f was not added, we conclude that
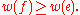
Let Y2 be the graph obtained by removing f from and adding e to Y1. It is easy to show that Y2 is connected, has the same number of edges as Y1, and the total weights of its edges is not larger than that of Y1, therefore it is also a minimum spanning tree of P and it contains e and all the edges added before it during the construction of V. Repeat the steps above and we will eventually obtain a minimum spanning tree of P that is identical to Y. This shows Y is a minimum spanning tree.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, Prim's algorithm is a greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
that finds a minimum spanning tree
Minimum spanning tree
Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...
for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
that includes every vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
, where the total weight of all the edges
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
in the tree is minimized. The algorithm was developed in 1930 by Czech
Czech people
Czechs, or Czech people are a western Slavic people of Central Europe, living predominantly in the Czech Republic. Small populations of Czechs also live in Slovakia, Austria, the United States, the United Kingdom, Chile, Argentina, Canada, Germany, Russia and other countries...
mathematician Vojtěch Jarník
Vojtech Jarník
Vojtěch Jarník was a Czech mathematician.His main area of work was in number theory and mathematical analysis; he proved a number of results on lattice point problems. He also developed the graph theory algorithm known as Prim's algorithm....
and later independently by computer scientist
Computer scientist
A computer scientist is a scientist who has acquired knowledge of computer science, the study of the theoretical foundations of information and computation and their application in computer systems....
Robert C. Prim
Robert C. Prim
Robert Clay Prim is an American mathematician and computer scientist.In 1941, Prim received his B.S. in Electrical Engineering from Princeton University. Later in 1949, he received his Ph.D. in Mathematics there also...
in 1957 and rediscovered by Edsger Dijkstra
Edsger Dijkstra
Edsger Wybe Dijkstra ; ) was a Dutch computer scientist. He received the 1972 Turing Award for fundamental contributions to developing programming languages, and was the Schlumberger Centennial Chair of Computer Sciences at The University of Texas at Austin from 1984 until 2000.Shortly before his...
in 1959. Therefore it is also sometimes called the DJP algorithm, the Jarník algorithm, or the Prim–Jarník algorithm.
Other algorithms for this problem include Kruskal's algorithm
Kruskal's algorithm
Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
and Borůvka's algorithm
Boruvka's algorithm
Borůvka's algorithm is an algorithm for finding a minimum spanning tree in a graph for which all edge weights are distinct.It was first published in 1926 by Otakar Borůvka as a method of constructing an efficient electricity network for Moravia....
.
Description
The only spanning tree of the empty graph (with an empty vertex set) is again the empty graph. The following description assumes that this special case is handled separately.The algorithm continuously increases the size of a tree, one edge at a time, starting with a tree consisting of a single vertex, until it spans all vertices.
- Input: A non-empty connected weighted graph with vertices V and edges E (the weights can be negative).
- Initialize: Vnew = {x}, where x is an arbitrary node (starting point) from V, Enew = {}
- Repeat until Vnew = V:
- Choose an edge (u, v) with minimal weight such that u is in Vnew and v is not (if there are multiple edges with the same weight, any of them may be picked)
- Add v to Vnew, and (u, v) to Enew
- Output: Vnew and Enew describe a minimal spanning tree
Time complexity
| Minimum edge weight data structure | Time complexity (total) |
|---|---|
| adjacency matrix Adjacency matrix In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices... , searching |
O(V2) |
| binary heap Binary heap A binary heap is a heap data structure created using a binary tree. It can be seen as a binary tree with two additional constraints:*The shape property: the tree is a complete binary tree; that is, all levels of the tree, except possibly the last one are fully filled, and, if the last level of... and adjacency list Adjacency list In graph theory, an adjacency list is the representation of all edges or arcs in a graph as a list.If the graph is undirected, every entry is a set of two nodes containing the two ends of the corresponding edge; if it is directed, every entry is a tuple of two nodes, one denoting the source node... |
O((V + E) log V) = O(E log V) |
| Fibonacci heap Fibonacci heap In computer science, a Fibonacci heap is a heap data structure consisting of a collection of trees. It has a better amortized running time than a binomial heap. Fibonacci heaps were developed by Michael L. Fredman and Robert E. Tarjan in 1984 and first published in a scientific journal in 1987... and adjacency list Adjacency list In graph theory, an adjacency list is the representation of all edges or arcs in a graph as a list.If the graph is undirected, every entry is a set of two nodes containing the two ends of the corresponding edge; if it is directed, every entry is a tuple of two nodes, one denoting the source node... |
O(E + V log V) |
A simple implementation using an adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
graph representation and searching an array of weights to find the minimum weight edge to add requires O(V2) running time. Using a simple binary heap
Binary heap
A binary heap is a heap data structure created using a binary tree. It can be seen as a binary tree with two additional constraints:*The shape property: the tree is a complete binary tree; that is, all levels of the tree, except possibly the last one are fully filled, and, if the last level of...
data structure and an adjacency list
Adjacency list
In graph theory, an adjacency list is the representation of all edges or arcs in a graph as a list.If the graph is undirected, every entry is a set of two nodes containing the two ends of the corresponding edge; if it is directed, every entry is a tuple of two nodes, one denoting the source node...
representation, Prim's algorithm can be shown to run in time O(E log V) where E is the number of edges and V is the number of vertices. Using a more sophisticated Fibonacci heap
Fibonacci heap
In computer science, a Fibonacci heap is a heap data structure consisting of a collection of trees. It has a better amortized running time than a binomial heap. Fibonacci heaps were developed by Michael L. Fredman and Robert E. Tarjan in 1984 and first published in a scientific journal in 1987...
, this can be brought down to O(E + V log V), which is asymptotically faster
Asymptotic computational complexity
In computational complexity theory, asymptotic computational complexity is the usage of the asymptotic analysis for the estimation of computational complexity of algorithms and computational problems, commonly associated with the usage of the big O notation....
when the graph is dense
Dense graph
In mathematics, a dense graph is a graph in which the number of edges is close to the maximal number of edges. The opposite, a graph with only a few edges, is a sparse graph...
enough that E is Ω(V).
Example run
| Image | Description |
|---|---|
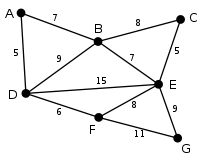 |
This is our original weighted graph. The numbers near the edges indicate their weight. |
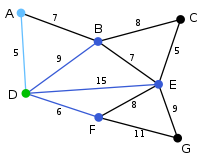 |
Vertex D has been arbitrarily chosen as a starting point. Vertices A, B, E and F are connected to D through a single edge. A is the vertex nearest to D and will be chosen as the second vertex along with the edge AD. |
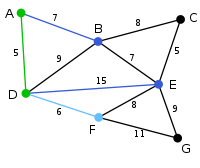 |
The next vertex chosen is the vertex nearest to either D or A. B is 9 away from D and 7 away from A, E is 15, and F is 6. F is the smallest distance away, so we highlight the vertex F and the arc DF. |
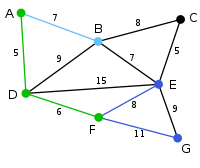 |
The algorithm carries on as above. Vertex B, which is 7 away from A, is highlighted. |
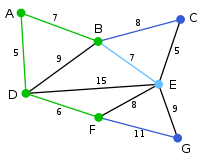 |
In this case, we can choose between C, E, and G. C is 8 away from B, E is 7 away from B, and G is 11 away from F. E is nearest, so we highlight the vertex E and the arc BE. |
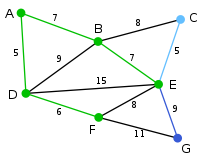 |
Here, the only vertices available are C and G. C is 5 away from E, and G is 9 away from E. C is chosen, so it is highlighted along with the arc EC. |
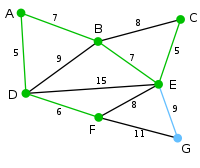 |
Vertex G is the only remaining vertex. It is 11 away from F, and 9 away from E. E is nearer, so we highlight G and the arc EG. |
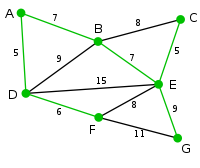 |
Now all the vertices have been selected and the minimum spanning tree Minimum spanning tree Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees... is shown in green. In this case, it has weight 39. |
| U | Edge(u,v) | V \ U |
|---|---|---|
| {} | {A,B,C,D,E,F,G} | |
| {D} | (D,A) = 5 V (D,B) = 9 (D,E) = 15 (D,F) = 6 |
{A,B,C,E,F,G} |
| {A,D} | (D,B) = 9 (D,E) = 15 (D,F) = 6 V (A,B) = 7 |
{B,C,E,F,G} |
| {A,D,F} | (D,B) = 9 (D,E) = 15 (A,B) = 7 V (F,E) = 8 (F,G) = 11 |
{B,C,E,G} |
| {A,B,D,F} | (B,C) = 8 (B,E) = 7 V (D,B) = 9 cycle (D,E) = 15 (F,E) = 8 (F,G) = 11 |
{C,E,G} |
| {A,B,D,E,F} | (B,C) = 8 (D,B) = 9 cycle (D,E) = 15 cycle (E,C) = 5 V (E,G) = 9 (F,E) = 8 cycle (F,G) = 11 |
{C,G} |
| {A,B,C,D,E,F} | (B,C) = 8 cycle (D,B) = 9 cycle (D,E) = 15 cycle (E,G) = 9 V (F,E) = 8 cycle (F,G) = 11 |
{G} |
| {A,B,C,D,E,F,G} | (B,C) = 8 cycle (D,B) = 9 cycle (D,E) = 15 cycle (F,E) = 8 cycle (F,G) = 11 cycle |
{} |
Proof of correctness
Let P be a connected, weighted graphGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. At every iteration of Prim's algorithm, an edge must be found that connects a vertex in a subgraph to a vertex outside the subgraph. Since P is connected, there will always be a path to every vertex. The output Y of Prim's algorithm is a tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, because the edge and vertex added to Y are connected. Let Y1 be a minimum spanning tree of P. If Y1=Y then Y is a minimum spanning tree. Otherwise, let e be the first edge added during the construction of Y that is not in Y1, and V be the set of vertices connected by the edges added before e. Then one endpoint of e is in V and the other is not. Since Y1 is a spanning tree of P, there is a path in Y1 joining the two endpoints. As one travels along the path, one must encounter an edge f joining a vertex in V to one that is not in V. Now, at the iteration when e was added to Y, f could also have been added and it would be added instead of e if its weight was less than e. Since f was not added, we conclude that
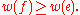
Let Y2 be the graph obtained by removing f from and adding e to Y1. It is easy to show that Y2 is connected, has the same number of edges as Y1, and the total weights of its edges is not larger than that of Y1, therefore it is also a minimum spanning tree of P and it contains e and all the edges added before it during the construction of V. Repeat the steps above and we will eventually obtain a minimum spanning tree of P that is identical to Y. This shows Y is a minimum spanning tree.

