Asymptotic computational complexity
Encyclopedia
In computational complexity theory
, asymptotic computational complexity is the usage of the asymptotic analysis
for the estimation of computational complexity of algorithm
s and computational problem
s, commonly associated with the usage of the big O notation
.
In terms of the most commonly estimated computational resource
s, it is spoken about the asymptotic time complexity
and asymptotic space complexity. Other asymptotically estimated resources include circuit complexity
and various measures of parallel computation, such as the number of (parallel) processors.
Since the groundlaying 1965 paper of Hartmanis
and Stearns
and the 1979 book by Garey and Johnson on NP-completeness, the term "computational complexity
" (of algorithms) most commonly refers to the asymptotic computational complexity.
Further, unless specified otherwise, the term "computational complexity" usually refers to the upper bound
for the asymptotic computational complexity of an algorithm or a problem, which is usually written in terms of the Big O notation
, e.g..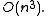
Other types of (asymptotic) computational complexity estimates are lower bounds ("Big Omega
" notation; e.g., Ω(n)) and asymptotically tight estimates, when the asymptotic upper and lower bounds coincide (written using the "Big Theta
"; e.g., Θ(n log n)).
A further tacit assumption is that the worst case analysis of computational complexity is in question unless stated otherwise. An alternative approach is probabilistic analysis of algorithms
.
In most practical cases deterministic algorithm
s or randomized algorithm
s are discussed, although theoretical computer science
also considers nondeterministic algorithm
s and other advanced models of computation.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, asymptotic computational complexity is the usage of the asymptotic analysis
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
for the estimation of computational complexity of algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s and computational problem
Computational problem
In theoretical computer science, a computational problem is a mathematical object representing a collection of questions that computers might want to solve. For example, the problem of factoring...
s, commonly associated with the usage of the big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
.
In terms of the most commonly estimated computational resource
Computational resource
In computational complexity theory, a computational resource is a resource used by some computational models in the solution of computational problems....
s, it is spoken about the asymptotic time complexity
Time complexity
In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
and asymptotic space complexity. Other asymptotically estimated resources include circuit complexity
Circuit complexity
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of Boolean circuits that compute them....
and various measures of parallel computation, such as the number of (parallel) processors.
Since the groundlaying 1965 paper of Hartmanis
Juris Hartmanis
Juris Hartmanis is a prominent computer scientist and computational theorist who, with Richard E. Stearns, received the 1993 ACM Turing Award "in recognition of their seminal paper which established the foundations for the field of computational complexity theory".Hartmanis was born in Latvia...
and Stearns
Richard Stearns (computer scientist)
Richard Edwin Stearns is a prominent computer scientist who, with Juris Hartmanis, received the 1993 ACM Turing Award "in recognition of their seminal paper which established the foundations for the field of computational complexity theory"...
and the 1979 book by Garey and Johnson on NP-completeness, the term "computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
" (of algorithms) most commonly refers to the asymptotic computational complexity.
Further, unless specified otherwise, the term "computational complexity" usually refers to the upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
for the asymptotic computational complexity of an algorithm or a problem, which is usually written in terms of the Big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, e.g..
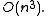Other types of (asymptotic) computational complexity estimates are lower bounds ("Big OmegaOmega
Omega is the 24th and last letter of the Greek alphabet. In the Greek numeric system, it has a value of 800. The word literally means "great O" , as opposed to omicron, which means "little O"...
" notation; e.g., Ω(n)) and asymptotically tight estimates, when the asymptotic upper and lower bounds coincide (written using the "Big Theta
Theta
Theta is the eighth letter of the Greek alphabet, derived from the Phoenician letter Teth...
"; e.g., Θ(n log n)).
A further tacit assumption is that the worst case analysis of computational complexity is in question unless stated otherwise. An alternative approach is probabilistic analysis of algorithms
Probabilistic analysis of algorithms
In analysis of algorithms, probabilistic analysis of algorithms is an approach to estimate the computational complexity of an algorithm or a computational problem. It starts from an assumption about a probabilistic distribution of the set of all possible inputs...
.
In most practical cases deterministic algorithm
Deterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
s or randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
s are discussed, although theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
also considers nondeterministic algorithm
Nondeterministic algorithm
In computer science, a nondeterministic algorithm is an algorithm that can exhibit different behaviors on different runs, as opposed to a deterministic algorithm. There are several ways an algorithm may behave differently from run to run. A concurrent algorithm can perform differently on different...
s and other advanced models of computation.