
Polarization of an algebraic form
Encyclopedia
In mathematics
, in particular in algebra
, polarization is a technique for expressing a homogeneous polynomial
in a simpler fashion by adjoining more variables. Specifically, given a homogeneous polynomial, polarization produces a multilinear form from which the original polynomial can be recovered by evaluating along a certain diagonal.
Although the technique is deceptively simple, it has applications in many areas of abstract mathematics: in particular to algebraic geometry
, invariant theory
, and representation theory
. Polarization and related techniques form the foundations for Weyl's invariant theory.
Let u(1), u(2), ..., u(d) be a collection of indeterminate
s with u(i) = (u1(i), u2(i), ..., un(i)), so that there are dn variables altogether. The polar form of f is a polynomial
which is linear separately in each u(i) (i.e., F is multilinear), symmetric in the u(i), and such that
The polar form of f is given by the following construction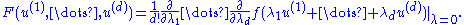
In other words, F is a constant multiple of the coefficient of λ1 λ2...λd in the expansion of f(λ1u(1) + ... + λdu(d)).
Then the polarization of f is a function in x(1) = (x(1), y(1)) and x(2) = (x(2), y(2)) given by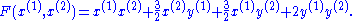
in which d! is a unit. In particular, it holds over any field
of characteristic zero or whose characteristic is strictly greater than d.
in n variables over k. Then A is graded by degree
, so that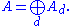
The polarization of algebraic forms then induces an isomorphism of vector spaces in each degree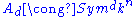
where Symd is the d-th symmetric power of the n-dimensional space kn.
These isomorphisms can be expressed independently of a basis as follows. If V is a finite-dimensional vector space and A is the ring of k-valued polynomial functions on V, graded by homogeneous degree, then polarization yields an isomorphism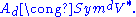
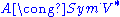
where Sym.V* is the full symmetric algebra
over V*.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular in algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, polarization is a technique for expressing a homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
in a simpler fashion by adjoining more variables. Specifically, given a homogeneous polynomial, polarization produces a multilinear form from which the original polynomial can be recovered by evaluating along a certain diagonal.
Although the technique is deceptively simple, it has applications in many areas of abstract mathematics: in particular to algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
, and representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
. Polarization and related techniques form the foundations for Weyl's invariant theory.
The technique
The fundamental ideas are as follows. Let f(u) be a polynomial in n variables u = (u1, u2, ..., un). Suppose that f is homogeneous of degree d, which means that- f(t u) = td f(u) for all t.
Let u(1), u(2), ..., u(d) be a collection of indeterminate
Indeterminate
Indeterminate has a variety of meanings in mathematics:* Indeterminate * Indeterminate system* Indeterminate equation* Statically indeterminate* Indeterminate formIt is also a term in botany and gardening:*Indeterminate growth...
s with u(i) = (u1(i), u2(i), ..., un(i)), so that there are dn variables altogether. The polar form of f is a polynomial
- F(u(1), u(2), ..., u(d))
which is linear separately in each u(i) (i.e., F is multilinear), symmetric in the u(i), and such that
- F(u,u, ..., u)=f(u).
The polar form of f is given by the following construction
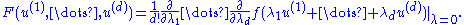
In other words, F is a constant multiple of the coefficient of λ1 λ2...λd in the expansion of f(λ1u(1) + ... + λdu(d)).
Examples
- Suppose that x=(x,y) and f(x) is the quadratic formQuadratic formIn mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
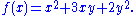
Then the polarization of f is a function in x(1) = (x(1), y(1)) and x(2) = (x(2), y(2)) given by
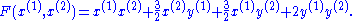
- More generally, if f is any quadratic form, then the polarization of f agrees with the conclusion of the polarization identityPolarization identityIn mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. Let \|x\| \, denote the norm of vector x and \langle x, \ y \rangle \, the inner product of vectors x and y...
.
- A cubic example. Let f(x,y)=x3 + 2xy2. Then the polarization of f is given by
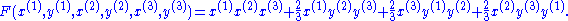
Mathematical details and consequences
The polarization of a homogeneous polynomial of degree d is valid over any commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
in which d! is a unit. In particular, it holds over any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristic zero or whose characteristic is strictly greater than d.
The polarization isomorphism (by degree)
For simplicity, let k be a field of characteristic zero and let A=k[x] be the polynomial ringPolynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
in n variables over k. Then A is graded by degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
, so that
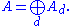
The polarization of algebraic forms then induces an isomorphism of vector spaces in each degree
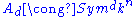
where Symd is the d-th symmetric power of the n-dimensional space kn.
These isomorphisms can be expressed independently of a basis as follows. If V is a finite-dimensional vector space and A is the ring of k-valued polynomial functions on V, graded by homogeneous degree, then polarization yields an isomorphism
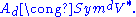
The algebraic isomorphism
Furthermore, the polarization is compatible with the algebraic structure on A, so that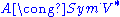
where Sym.V* is the full symmetric algebra
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
over V*.
Remarks
- For fields of positive characteristic p, the foregoing isomorphisms apply if the graded algebras are truncated at degree p-1.
- There do exist generalizations when V is an infinite dimensional topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
.

