
Poisson's ratio
Encyclopedia
Poisson's ratio named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain
(perpendicular to the applied load), to the extension or axial strain (in the direction of the applied load).
When a material is compressed in one direction, it usually tends to expand in the other two directions perpendicular to the direction of compression. This phenomenon is called the Poisson effect. Poisson's ratio (nu
(nu
) is a measure of the Poisson effect. The Poisson ratio is the ratio of the fraction (or percent) of expansion divided by the fraction (or percent) of compression, for small values of these changes.
Conversely, if the material is stretched rather than compressed, it usually tends to contract in the directions transverse to the direction of stretching. Again, the Poisson ratio will be the ratio of relative contraction to relative stretching, and will have the same value as above. In certain rare cases, a material will actually shrink in the transverse direction when compressed (or expand when stretched) which will yield a negative value of the Poisson ratio.
The Poisson's ratio of a stable, isotropic, linear elastic
material cannot be less than −1.0 nor greater than 0.5 due to the requirement that Young's modulus
, the shear modulus and bulk modulus
have positive values. Most materials have Poisson's ratio values ranging between 0.0 and 0.5. A perfectly incompressible material deformed elastically at small strains would have a Poisson's ratio of exactly 0.5. Most steels and rigid polymers when used within their design limits (before yield
) exhibit values of about 0.3, increasing to 0.5 for post-yield deformation (which occurs largely at constant volume.) Rubber has a Poisson ratio of nearly 0.5. Cork's Poisson ratio is close to 0: showing very little lateral expansion when compressed. Some materials, mostly polymer foams, have a negative Poisson's ratio; if these auxetic materials
are stretched in one direction, they become thicker in perpendicular directions. Some anisotropic materials have one or more Poisson ratios above 0.5 in some directions.
Assuming that the material is stretched or compressed along the axial direction (the x axis in the diagram):
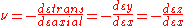
where is the resulting Poisson's ratio,
is the resulting Poisson's ratio,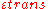 is transverse strain (negative for axial tension (stretching), positive for axial compression)
is transverse strain (negative for axial tension (stretching), positive for axial compression) is axial strain (positive for axial tension, negative for axial compression).
is axial strain (positive for axial tension, negative for axial compression).
. When the bonds elongate in the direction of load , they shorten in the other directions. This behavior multiplied many times throughout the material lattice is what drives the phenomenon.
 in the x direction, and a length decrease of
in the x direction, and a length decrease of 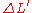 in the y and z directions, the infinitesimal diagonal strains are given by:
in the y and z directions, the infinitesimal diagonal strains are given by:
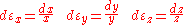
Integrating the definition of Poisson's ratio:

Solving and exponentiating, the relationship between and
and 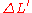 is found to be:
is found to be:
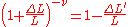
For very small values of and
and  , the first-order approximation yields:
, the first-order approximation yields:
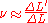
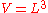 and
and  :
:
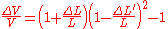
Using the above derived relationship between and
and 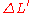 :
:
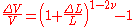
and for very small values of and
and 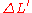 , the first-order approximation yields:
, the first-order approximation yields:
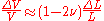
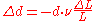
The above formula is true only in the case of small deformations; if deformations are large then the following (more precise) formula can be used:
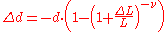
where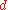 is original diameter
is original diameter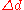 is rod diameter change
is rod diameter change is Poisson's ratio
is Poisson's ratio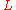 is original length, before stretch
is original length, before stretch is the change of length.
is the change of length.
The value is negative because it decrease with increase of length
(for compressive forces) into three dimensions: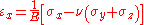

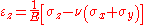
or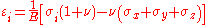
where ,
, 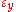 and
and 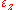 are strain
are strain
in the direction of ,
, 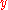 and
and  axis
axis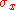 ,
, 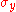 and
and  are stress
are stress
in the direction of ,
, 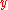 and
and  axis
axis is Young's modulus
is Young's modulus
(the same in all directions: ,
, 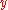 and
and  for isotropic materials)
for isotropic materials) is Poisson's ratio (the same in all directions:
is Poisson's ratio (the same in all directions:  ,
, 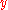 and
and  for isotropic materials)
for isotropic materials)
These equations will hold in the general case which includes shear forces as well as compressive forces, and the full generalization of Hooke's law is given by:
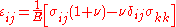
where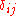 is the Kronecker delta and
is the Kronecker delta and
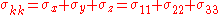
s such as wood, Hooke's law
can be expressed in matrix
form as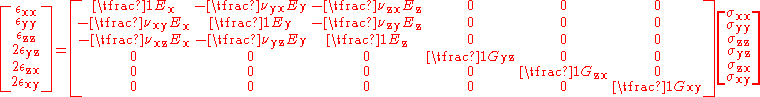
where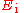 is the Young's modulus
is the Young's modulus
along axis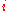
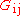 is the shear modulus in direction
is the shear modulus in direction 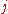 on the plane whose normal is in direction
on the plane whose normal is in direction 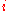
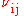 is the Poisson's ratio that corresponds to a contraction in direction
is the Poisson's ratio that corresponds to a contraction in direction 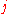 when an extension is applied in direction
when an extension is applied in direction  .
.
The Poisson's ratio of an orthotropic material is different in each direction (x, y and z). However, the symmetry of the stress and strain tensors implies that not all the six Poisson's ratios in the equation are independent. There are only nine independent material properties; three elastic moduli, three shear moduli, and three Poisson's ratios. The remaining three Poisson's ratios can be obtained from the relations

From the above relations we can see that if then
then  . The larger Poisson's ratio (in this case
. The larger Poisson's ratio (in this case  ) is called the major Poisson's ratio while the smaller one (in this case
) is called the major Poisson's ratio while the smaller one (in this case 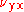 ) is called the minor Poisson's ratio. We can find similar relations between the other Poisson's ratios.
) is called the minor Poisson's ratio. We can find similar relations between the other Poisson's ratios.
 , then Hookes's law takes the form
, then Hookes's law takes the form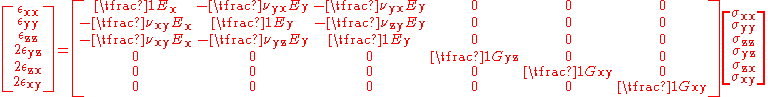
where we have used the plane of symmetry to reduce the number of constants, i.e.,
to reduce the number of constants, i.e., 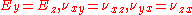 .
.
The symmetry of the stress and strain tensors implies that
This leaves us with six independent constants . However, transverse isotropy gives rise to a further constraint between
. However, transverse isotropy gives rise to a further constraint between 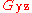 and
and 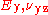 which is
which is
Therefore, there are five independent elastic material properties two of which are Poisson's ratios. For the assumed plane of symmetry, the larger of and
and 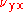 is the major Poisson's ratio. The other major and minor Poisson's ratios are equal.
is the major Poisson's ratio. The other major and minor Poisson's ratios are equal.
Another area of application for Poisson's effect is in the realm of structural geology
. Rocks, like most materials, are subject to Poisson's effect while under stress. In a geological timescale, excessive erosion or sedimentation of Earth's crust can either create or remove large vertical stresses upon the underlying rock. This rock will expand or contract in the vertical direction as a direct result of the applied stress, and it will also deform in the horizontal direction as a result of Poisson's effect. This change in strain in the horizontal direction can affect or form joints and dormant stresses in the rock.
The use of cork as a stopper for wine bottles is the result of the fact that cork has a Poisson ratio of practically zero. This means that, as the cork is inserted into the bottle, the upper part which is not yet inserted will not expand as the lower part is compressed. The force needed to insert a cork into a bottle arises only from the compression of the cork and the friction between the cork and the bottle. If the stopper were made of rubber, for example, (with a Poisson ratio of about 1/2), there would be a relatively large additional force required to overcome the expansion of the upper part of the rubber stopper.
Strain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
(perpendicular to the applied load), to the extension or axial strain (in the direction of the applied load).
When a material is compressed in one direction, it usually tends to expand in the other two directions perpendicular to the direction of compression. This phenomenon is called the Poisson effect. Poisson's ratio
 (nu
(nuNu (letter)
Nu , is the 13th letter of the Greek alphabet. In the system of Greek numerals it has a value of 50...
) is a measure of the Poisson effect. The Poisson ratio is the ratio of the fraction (or percent) of expansion divided by the fraction (or percent) of compression, for small values of these changes.
Conversely, if the material is stretched rather than compressed, it usually tends to contract in the directions transverse to the direction of stretching. Again, the Poisson ratio will be the ratio of relative contraction to relative stretching, and will have the same value as above. In certain rare cases, a material will actually shrink in the transverse direction when compressed (or expand when stretched) which will yield a negative value of the Poisson ratio.
The Poisson's ratio of a stable, isotropic, linear elastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
material cannot be less than −1.0 nor greater than 0.5 due to the requirement that Young's modulus
Young's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
, the shear modulus and bulk modulus
Bulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
have positive values. Most materials have Poisson's ratio values ranging between 0.0 and 0.5. A perfectly incompressible material deformed elastically at small strains would have a Poisson's ratio of exactly 0.5. Most steels and rigid polymers when used within their design limits (before yield
Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
) exhibit values of about 0.3, increasing to 0.5 for post-yield deformation (which occurs largely at constant volume.) Rubber has a Poisson ratio of nearly 0.5. Cork's Poisson ratio is close to 0: showing very little lateral expansion when compressed. Some materials, mostly polymer foams, have a negative Poisson's ratio; if these auxetic materials
Auxetics
Auxetics are materials that have a negative Poisson's ratio. When stretched, they become thicker perpendicular to the applied force. This occurs due to their hinge-like structures, which flex when stretched...
are stretched in one direction, they become thicker in perpendicular directions. Some anisotropic materials have one or more Poisson ratios above 0.5 in some directions.
Assuming that the material is stretched or compressed along the axial direction (the x axis in the diagram):
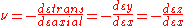
where
 is the resulting Poisson's ratio,
is the resulting Poisson's ratio,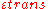 is transverse strain (negative for axial tension (stretching), positive for axial compression)
is transverse strain (negative for axial tension (stretching), positive for axial compression) is axial strain (positive for axial tension, negative for axial compression).
is axial strain (positive for axial tension, negative for axial compression).Cause of Poisson’s effect
On the molecular level, Poisson’s effect is caused by slight movements between molecules and the stretching of molecular bonds within the material lattice to accommodate the stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
. When the bonds elongate in the direction of load , they shorten in the other directions. This behavior multiplied many times throughout the material lattice is what drives the phenomenon.
Length change
For a cube stretched in the x-direction (see figure 1) with a length increase of in the x direction, and a length decrease of
in the x direction, and a length decrease of 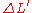 in the y and z directions, the infinitesimal diagonal strains are given by:
in the y and z directions, the infinitesimal diagonal strains are given by: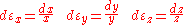
Integrating the definition of Poisson's ratio:

Solving and exponentiating, the relationship between
 and
and 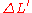 is found to be:
is found to be: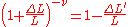
For very small values of
 and
and  , the first-order approximation yields:
, the first-order approximation yields: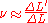
Volumetric change
The relative change of volume ΔV/V due to the stretch of the material can now be calculated. Using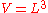 and
and  :
: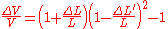
Using the above derived relationship between
 and
and 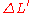 :
: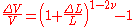
and for very small values of
 and
and 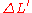 , the first-order approximation yields:
, the first-order approximation yields: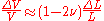
Width change
If a rod with diameter (or width, or thickness) d and length L is subject to tension so that its length will change by ΔL then its diameter d will change by: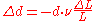
The above formula is true only in the case of small deformations; if deformations are large then the following (more precise) formula can be used:
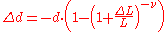
where
 is original diameter
is original diameter is rod diameter change
is rod diameter change is Poisson's ratio
is Poisson's ratio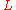 is original length, before stretch
is original length, before stretch is the change of length.
is the change of length.The value is negative because it decrease with increase of length
Isotropic materials
For a linear isotropic material subjected only to compressive (i.e. normal) forces, the deformation of a material in the direction of one axis will produce a deformation of the material along the other axis in three dimensions. Thus it is possible to generalize Hooke's LawHooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
(for compressive forces) into three dimensions:
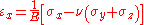

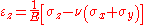
or
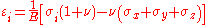
where
 ,
, 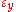 and
and 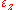 are strain
are strainStrain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
in the direction of
 ,
, 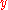 and
and  axis
axis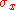 ,
, 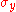 and
and  are stress
are stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
in the direction of
 ,
, 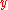 and
and  axis
axis is Young's modulus
is Young's modulusYoung's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
(the same in all directions:
 ,
, 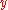 and
and  for isotropic materials)
for isotropic materials) is Poisson's ratio (the same in all directions:
is Poisson's ratio (the same in all directions:  ,
, 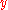 and
and  for isotropic materials)
for isotropic materials)These equations will hold in the general case which includes shear forces as well as compressive forces, and the full generalization of Hooke's law is given by:
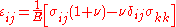
where
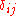 is the Kronecker delta and
is the Kronecker delta and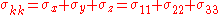
Orthotropic materials
For orthotropic materialOrthotropic material
An orthotropic material has two or three mutually orthogonal twofold axes of rotational symmetry so that its mechanical properties are, in general, different along each axis. Orthotropic materials are thus anisotropic; their properties depend on the direction in which they are measured...
s such as wood, Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
can be expressed in matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
form as
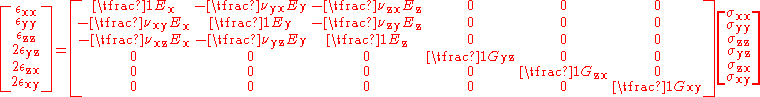
where
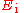 is the Young's modulus
is the Young's modulusYoung's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
along axis
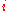
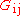 is the shear modulus in direction
is the shear modulus in direction 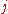 on the plane whose normal is in direction
on the plane whose normal is in direction 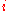
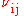 is the Poisson's ratio that corresponds to a contraction in direction
is the Poisson's ratio that corresponds to a contraction in direction 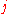 when an extension is applied in direction
when an extension is applied in direction  .
.The Poisson's ratio of an orthotropic material is different in each direction (x, y and z). However, the symmetry of the stress and strain tensors implies that not all the six Poisson's ratios in the equation are independent. There are only nine independent material properties; three elastic moduli, three shear moduli, and three Poisson's ratios. The remaining three Poisson's ratios can be obtained from the relations

From the above relations we can see that if
 then
then  . The larger Poisson's ratio (in this case
. The larger Poisson's ratio (in this case  ) is called the major Poisson's ratio while the smaller one (in this case
) is called the major Poisson's ratio while the smaller one (in this case 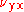 ) is called the minor Poisson's ratio. We can find similar relations between the other Poisson's ratios.
) is called the minor Poisson's ratio. We can find similar relations between the other Poisson's ratios.Transversely isotropic materials
Transversely isotropic materials have a plane of symmetry in which the elastic properties are isotropic. If we assume that this plane of symmetry is , then Hookes's law takes the form
, then Hookes's law takes the form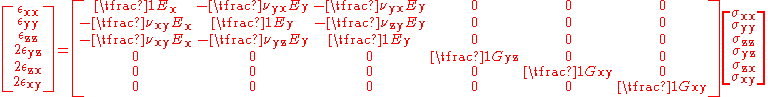
where we have used the plane of symmetry
 to reduce the number of constants, i.e.,
to reduce the number of constants, i.e., 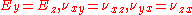 .
.The symmetry of the stress and strain tensors implies that

This leaves us with six independent constants
 . However, transverse isotropy gives rise to a further constraint between
. However, transverse isotropy gives rise to a further constraint between 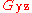 and
and 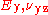 which is
which is
Therefore, there are five independent elastic material properties two of which are Poisson's ratios. For the assumed plane of symmetry, the larger of
 and
and 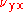 is the major Poisson's ratio. The other major and minor Poisson's ratios are equal.
is the major Poisson's ratio. The other major and minor Poisson's ratios are equal.Poisson's ratio values for different materials

Negative Poisson's ratio materials
Some materials known as auxetic materials display a negative Poisson’s ratio. When subjected to positive strain in a longitudinal axis, the transverse strain in the material will actually be positive (i.e. it would increase the cross sectional area). For these materials, it is usually due to uniquely oriented, hinged molecular bonds. In order for these bonds to stretch in the longitudinal direction, the hinges must ‘open’ in the transverse direction, effectively exhibiting a positive strain.Applications of Poisson's effect
One area in which Poisson's effect has a considerable influence is in pressurized pipe flow. When the air or liquid inside a pipe is highly pressurized it exerts a uniform force on the inside of the pipe, resulting in a radial stress within the pipe material. Due to Poisson's effect, this radial stress will cause the pipe to slightly increase in diameter and decrease in length. The decrease in length, in particular, can have a noticeable effect upon the pipe joints, as the effect will accumulate for each section of pipe joined in series. A restrained joint may be pulled apart or otherwise prone to failure.Another area of application for Poisson's effect is in the realm of structural geology
Structural geology
Structural geology is the study of the three-dimensional distribution of rock units with respect to their deformational histories. The primary goal of structural geology is to use measurements of present-day rock geometries to uncover information about the history of deformation in the rocks, and...
. Rocks, like most materials, are subject to Poisson's effect while under stress. In a geological timescale, excessive erosion or sedimentation of Earth's crust can either create or remove large vertical stresses upon the underlying rock. This rock will expand or contract in the vertical direction as a direct result of the applied stress, and it will also deform in the horizontal direction as a result of Poisson's effect. This change in strain in the horizontal direction can affect or form joints and dormant stresses in the rock.
The use of cork as a stopper for wine bottles is the result of the fact that cork has a Poisson ratio of practically zero. This means that, as the cork is inserted into the bottle, the upper part which is not yet inserted will not expand as the lower part is compressed. The force needed to insert a cork into a bottle arises only from the compression of the cork and the friction between the cork and the bottle. If the stopper were made of rubber, for example, (with a Poisson ratio of about 1/2), there would be a relatively large additional force required to overcome the expansion of the upper part of the rubber stopper.
See also
- 3-D elasticity
- Hooke's LawHooke's lawIn mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
- Impulse excitation techniqueImpulse excitation technique-Practical:The impulse excitation technique is a nondestructive test method that uses natural frequency, dimensions and mass of a test-piece to determine Young's modulus, Shear modulus, Poisson's ratio and damping coefficient....
- Orthotropic materialOrthotropic materialAn orthotropic material has two or three mutually orthogonal twofold axes of rotational symmetry so that its mechanical properties are, in general, different along each axis. Orthotropic materials are thus anisotropic; their properties depend on the direction in which they are measured...
- Coefficient of thermal expansion

