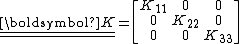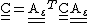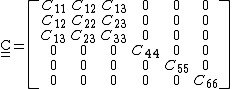Orthotropic material
Encyclopedia

Material
Material is anything made of matter, constituted of one or more substances. Wood, cement, hydrogen, air and water are all examples of materials. Sometimes the term "material" is used more narrowly to refer to substances or components with certain physical properties that are used as inputs to...
has two or three mutually orthogonal twofold axes of rotational symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
so that its mechanical properties are, in general, different along each axis. Orthotropic materials are thus anisotropic; their properties depend on the direction in which they are measured. An isotropic material, in contrast, has the same properties in every direction.
One common example of an orthotropic material with two axis of symmetry would be a polymer reinforced by parallel glass or graphite fibers. The strength and stiffness of such a composite material will usually be greater in a direction parallel to the fibers than in the transverse direction. Another example would be a biological membrane, in which the properties in the plane of the membrane will be different from those in the perpendicular direction. Such materials are sometimes called transverse isotropic
Transverse isotropy
A transversely isotropic material is one with physical properties which are symmetric about an axis that is normal to a plane of isotropy. This transverse plane has infinite planes of symmetry and thus, within this plane, the material properties are same in all directions...
.
A familiar example of an orthotropic material with three mutually perpendicular axis is wood, in which the properties (such as strength and stiffness) along its grain and in each of the two perpendicular directions are different. Hankinson's equation
Hankinson's equation
Hankinson's equation is a mathematical relationship for predicting the off-axis uniaxial compressive strength of wood. The formula can also be used to compute the fiber stress or the stress wave velocity at the elastic limit as a function of grain angle in wood...
provides a means to quantify the difference in strength in different directions. Another example is a metal which has been rolled to form a sheet; the properties in the rolling direction and each of the two transverse directions will be different due to the anisotropic structure that develops during rolling.
It is important to keep in mind that a material which is anisotropic on one length scale may be isotropic on another (usually larger) length scale. For instance, most metals are polycrystalline with very small grains
Crystallite
Crystallites are small, often microscopic crystals that, held together through highly defective boundaries, constitute a polycrystalline solid. Metallurgists often refer to crystallites as grains.- Details :...
. Each of the individual grains may be anisotropic, but if the material as a whole comprises many randomly oriented grains, then its measured mechanical properties will be an average of the properties over all possible orientations of the individual grains.
Anisotropic material relations
Material behavior is represented in physical theories by constitutive relations. A large class of physical behaviors can be represented by linear material models that take the form of a second-order tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
. The material tensor provides a relation between two vectors and can be written as
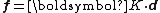
where
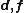 are two vectors representing physical quantities and
are two vectors representing physical quantities and 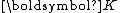 is the second-order material tensor. If we express the above equation in terms of components with respect to an orthonormal coordinate system
is the second-order material tensor. If we express the above equation in terms of components with respect to an orthonormal coordinate systemCoordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
, we can write
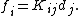
Summation over repeated indices has been assumed in the above relation. In matrix form we have
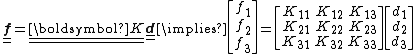
Examples of physical problems that fit the above template are listed in the table below.
| Problem | 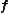 | 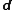 | 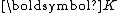 |
|---|---|---|---|
| Electrical conduction | Electrical current 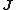 |
Electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... 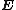 |
Electrical conductivity 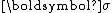 |
| Dielectric Dielectric A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric... s |
Electrical displacement 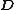 |
Electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... 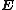 |
Electric permittivity 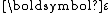 |
| Magnetism Magnetism Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well... |
Magnetic induction Magnetic induction Magnetic induction may refer to one of the following:* Electromagnetic induction* Magnetic field B is sometimes called magnetic induction... 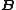 |
Magnetic field Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... 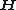 |
Magnetic permeability 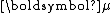 |
| Thermal conduction | Heat flux Heat flux Heat flux or thermal flux is the rate of heat energy transfer through a given surface. The SI derived unit of heat rate is joule per second, or watt. Heat flux is the heat rate per unit area. In SI units, heat flux is measured in W/m2]. Heat rate is a scalar quantity, while heat flux is a vectorial... 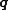 |
Temperature gradient Temperature gradient A temperature gradient is a physical quantity that describes in which direction and at what rate the temperature changes the most rapidly around a particular location. The temperature gradient is a dimensional quantity expressed in units of degrees per unit length... 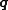 |
Thermal conductivity Thermal conductivity In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction.... 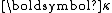 |
| Diffusion Diffusion Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles... |
Particle flux Flux In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time... 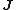 |
Concentration gradient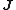 |
Diffusivity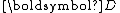 |
| Flow Fluid dynamics In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics... in porous media |
Weighted fluid velocity Velocity In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ... 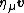 |
Pressure gradient Pressure gradient In atmospheric sciences , the pressure gradient is a physical quantity that describes in which direction and at what rate the pressure changes the most rapidly around a particular location. The pressure gradient is a dimensional quantity expressed in units of pressure per unit length... 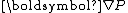 |
Fluid permeability 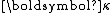 |
Condition for material symmetry
The material matrix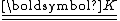 has a symmetry with respect to a given orthogonal transformation (
has a symmetry with respect to a given orthogonal transformation (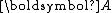 ) if it does not change when subjected to that transformation.
) if it does not change when subjected to that transformation.For invariance of the material properties under such a transformation we require
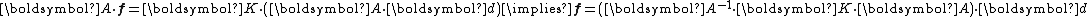
Hence the condition for material symmetry is (using the definition of an orthogonal transformation)
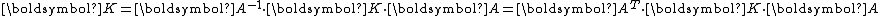
Orthogonal transformations can be represented in Cartesian coordinates by a
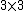 matrix
matrix 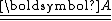 given by
given by
Therefore the symmetry condition can be written in matrix form as
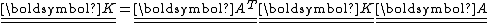
Orthotropic material properties
An orthotropic material has three orthogonal symmetry planes. If we choose an orthonormal coordinate system such that the axes coincide with the normals to the three symmetry planes, the transformation matrices are
It can be shown that if the matrix
 for a material is invariant under reflection about two orthogonal planes then it is also invariant under reflection about the third orthogonal plane.
for a material is invariant under reflection about two orthogonal planes then it is also invariant under reflection about the third orthogonal plane.Consider the reflection
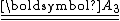 about the
about the  plane. Then we have
plane. Then we have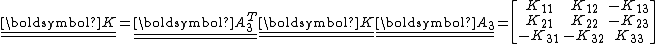
The above relation implies that
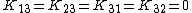 . Next consider a reflection
. Next consider a reflection  about the
about the 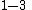 plane. We then have
plane. We then have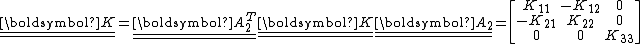
That implies that
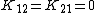 . Therefore the material properties of an orthotropic material are described by the matrix
. Therefore the material properties of an orthotropic material are described by the matrixAnisotropic elasticity
In linear elasticityLinear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
, the relation between stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
and strain depend on the type of material under consideration. This relation is known as Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
. For anisotropic materials Hooke's law can be written as
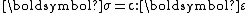
where
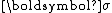 is the stress tensor
is the stress tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
,
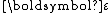 is the strain tensor, and
is the strain tensor, and  is the elastic stiffness tensor. If the tensors in the above expression are described in terms of components with respect to an orthonormal coordinate system
is the elastic stiffness tensor. If the tensors in the above expression are described in terms of components with respect to an orthonormal coordinate systemCoordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
we can write
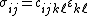
where summation has been assumed over repeated indices. Since the stress and strain tensors are symmetric, and since the stress-strain relation in linear elasticity can be derived from a strain energy density function
Strain energy density function
A strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
, the following symmetries hold for linear elastic materials

Because of the above symmetries, the stress-strain relation for linear elastic materials can be expressed in matrix form as
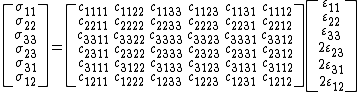
An alternative representation in Voigt notation
Voigt notation
In mathematics, Voigt notation or Voigt form in multilinear algebra is a way to represent a symmetric tensor by reducing its order. There are a few variants and associated names for this idea: Mandel notation, Mandel–Voigt notation and Nye notation are others found. Kelvin notation is a revival by...
is
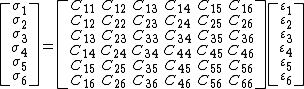
or
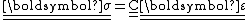
The stiffness matrix
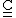 in the above relation satisfies point symmetry .
in the above relation satisfies point symmetry .Condition for material symmetry
The stiffness matrix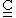 satisfies a given symmetry condition if it does not change when subjected to the corresponding orthogonal transformation. The orthogonal transformation may represent symmetry with respect to a point, an axis, or a plane. Orthogonal transformations in linear elasticity include rotations and reflections, but not shape changing transformations and can be represented, in orthonormal coordinates, by a
satisfies a given symmetry condition if it does not change when subjected to the corresponding orthogonal transformation. The orthogonal transformation may represent symmetry with respect to a point, an axis, or a plane. Orthogonal transformations in linear elasticity include rotations and reflections, but not shape changing transformations and can be represented, in orthonormal coordinates, by a  matrix
matrix 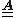 given by
given by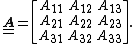
In Voigt notation, the transformation matrix for the stress tensor can be expressed as a
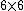 matrix
matrix 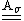 given by
given by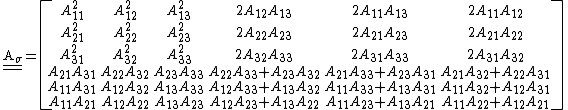
The transformation for the strain tensor has a slightly different form because of the choice of notation. This transformation matrix is
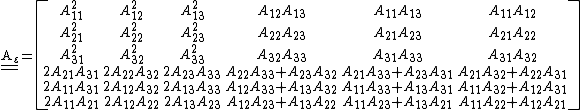
It can be shown that
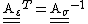 .
.
The elastic properties of a continuum are invariant under an orthogonal transformationif and only if
Stiffness and compliance matrices in orthotropic elasticity
An orthotropic elastic material has three orthogonal symmetry planes. If we choose an orthonormal coordinate system such that the axes coincide with the normals to the three symmetry planes, the transformation matrices are
We can show that if the matrix
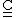 for a linear elastic material is invariant under reflection about two orthogonal planes then it is also invariant under reflection about the third orthogonal plane.
for a linear elastic material is invariant under reflection about two orthogonal planes then it is also invariant under reflection about the third orthogonal plane.If we consider the reflection
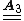 about the
about the 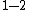 plane, then we have
plane, then we have
Then the requirement
 implies that
implies that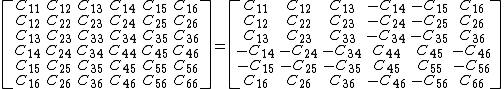
The above requirement can be satisfied only if
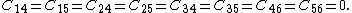
Let us next consider the reflection
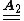 about the
about the 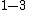 plane. In that case
plane. In that case
Using the invariance condition again, we get the additional requirement that
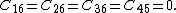
No further information can be obtained because the reflection about third symmetry plane is not independent of reflections about the planes that we have already considered. Therefore, the stiffness matrix of an orthotropic linear elastic material can be written as
The inverse of this matrix is commonly written as
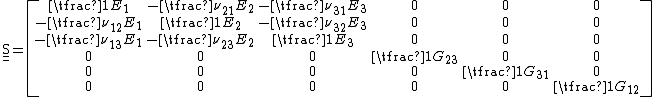
where
 is the Young's modulus
is the Young's modulusYoung's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
along axis
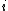 ,
, 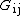 is the shear modulus in direction
is the shear modulus in direction 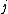 on the plane whose normal is in direction
on the plane whose normal is in direction 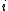 , and
, and 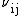 is the Poisson's ratio
is the Poisson's ratioPoisson's ratio
Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
that corresponds to a contraction in direction
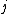 when an extension is applied in direction
when an extension is applied in direction 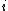 .
.Bounds on the moduli of orthotropic elastic materials
The strain-stress relation for orthotropic linear elastic materials can be written in Voigt notation as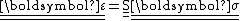
where the compliance matrix
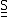 is given by
is given by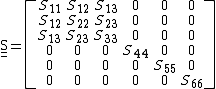
The compliance matrix is symmetric and must be positive definite for the strain energy density
Strain energy density function
A strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
to be positive. This implies from Sylvester's criterion
Sylvester's criterion
In mathematics, Sylvester’s criterion is a necessary and sufficient criterion to determine whether a Hermitian matrix is positive-definite. It is named after James Joseph Sylvester....
that all the principal minor
Minor (linear algebra)
In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns...
s of the matrix are positive, i.e.,

where
 is the
is the 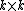 principal submatrix of
principal submatrix of 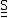 .
.Then,
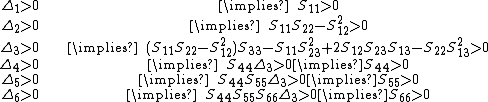
We can show that this set of conditions implies that
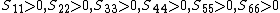
or
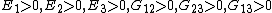
However, no similar lower bounds can be placed on the values of the Poisson's ratios
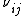 .
.See also
- AnisotropyAnisotropyAnisotropy is the property of being directionally dependent, as opposed to isotropy, which implies identical properties in all directions. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties An example of anisotropy is the light...
- Stress (mechanics)
- Infinitesimal strain theory
- Finite strain theory
- Hooke's lawHooke's lawIn mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
Further reading
- Orthotropy modeling equations from OOFEMOOFEMOOFEM is an open source multi-physics finite element code with object oriented architecture. The aim of this project is to provide efficient and robust tool for FEM computations as well as to offer highly modular and extensible environment for development....
Matlib manual section. - Hooke's law for orthotropic materials