
Plimpton 322
Encyclopedia

Babylonia
Babylonia was an ancient cultural region in central-southern Mesopotamia , with Babylon as its capital. Babylonia emerged as a major power when Hammurabi Babylonia was an ancient cultural region in central-southern Mesopotamia (present-day Iraq), with Babylon as its capital. Babylonia emerged as...
n clay tablet
Clay tablet
In the Ancient Near East, clay tablets were used as a writing medium, especially for writing in cuneiform, throughout the Bronze Age and well into the Iron Age....
, notable as containing an example of Babylonian mathematics
Babylonian mathematics
Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
. It has number 322 in the G.A. Plimpton Collection at Columbia University
Columbia University
Columbia University in the City of New York is a private, Ivy League university in Manhattan, New York City. Columbia is the oldest institution of higher learning in the state of New York, the fifth oldest in the United States, and one of the country's nine Colonial Colleges founded before the...
. This tablet, believed to have been written about 1800 BC
18th century BC
The 18th century BCE was the century which lasted from 1800 BCE to 1701 BCE.-Events:*1800 BCE: Iron age in India*1800 BCE: Beginning of the Nordic Bronze Age in the period system devised by Oscar Montelius....
, has a table of four columns and 15 rows of numbers in the cuneiform script
Cuneiform script
Cuneiform script )) is one of the earliest known forms of written expression. Emerging in Sumer around the 30th century BC, with predecessors reaching into the late 4th millennium , cuneiform writing began as a system of pictographs...
of the period.
This table lists what are now called Pythagorean triples, i.e., integers a, b, c satisfying
 . The triples are too many to have been constructed by brute force. From a modern perspective, a method for constructing such triples is a significant early achievement, known before only among the Greeks. At the same time, one should recall the tablet's author was a scribe, rather than a professional mathematician; it has been suggested that one of his goals may have been to produce examples for school problems.
. The triples are too many to have been constructed by brute force. From a modern perspective, a method for constructing such triples is a significant early achievement, known before only among the Greeks. At the same time, one should recall the tablet's author was a scribe, rather than a professional mathematician; it has been suggested that one of his goals may have been to produce examples for school problems.Although the tablet was interpreted in the past as a trigonometric table, more recently published work sees this as anachronistic, and gives it a different function. For readable popular treatments of this tablet see or, more briefly, . is a more detailed and technical discussion of the interpretation of the tablet's numbers, with an extensive bibliography.
Provenance and dating
Plimpton 322 is partly broken, approximately 13 cm wide, 9 cm tall, and 2 cm thick. New York publisher George Arthur PlimptonGeorge Arthur Plimpton
George Arthur Plimpton was an American publisher and philanthropist.Plimpton was born in Walpole, Massachusetts, the son and grandson of iron manufacturers. He graduated from the Phillips Exeter Academy in 1873 and Amherst College in 1876...
purchased the tablet from an archaeological dealer, Edgar J. Banks
Edgar James Banks
Edgar James Banks . American diplomat, antiquarian and novelist. Banks was an antiquities enthusiast and entrepreneurial roving archaeologist in the closing days of the Ottoman Empire, who has been held up as an original for the fictional composite figure of Indiana Jones...
, in about 1922, and bequeathed it with the rest of his collection to Columbia University
Columbia University
Columbia University in the City of New York is a private, Ivy League university in Manhattan, New York City. Columbia is the oldest institution of higher learning in the state of New York, the fifth oldest in the United States, and one of the country's nine Colonial Colleges founded before the...
in the mid 1930s. According to Banks, the tablet came from Senkereh, a site in southern Iraq corresponding to the ancient city of Larsa
Larsa
Larsa was an important city of ancient Sumer, the center of the cult of the sun god Utu. It lies some 25 km southeast of Uruk in Iraq's Dhi Qar Governorate, near the east bank of the Shatt-en-Nil canal at the site of the modern settlement Tell as-Senkereh or Sankarah.-History:According to...
.
The tablet is believed to have been written about 1800 BC, based in part on the style of handwriting used for its cuneiform script
Cuneiform script
Cuneiform script )) is one of the earliest known forms of written expression. Emerging in Sumer around the 30th century BC, with predecessors reaching into the late 4th millennium , cuneiform writing began as a system of pictographs...
: writes that this handwriting "is typical of documents from southern Iraq of 4000–3500 years ago." More specifically, based on formatting similarities with other tablets from Larsa that have explicit dates written on them, Plimpton 322 can be dated to the period 1822–1784 BC. Robson
Eleanor Robson
Eleanor Robson is a Reader in History and Philosophy of Science at the Department of History and Philosophy of Science, Cambridge University, vice-chair of the British School of Archaeology in Iraq and a Quondam Fellow of All Souls College, Oxford....
points out that Plimpton 322 was written in the same format as other administrative, rather than mathematical, documents of the period.
Content
The main content of Plimpton 322 is a table of numbers, with four columns and fifteen rows, in Babylonian sexagesimal notation. The fourth column is just a row number, in order from 1 to 15. The second and third columns are completely visible in the surviving tablet. However, the edge of the first column has been broken off, and there are two consistent extrapolations for what the missing digits could be; these interpretations differ only in whether or not each number starts with an additional digit equal to 1. With the differing extrapolations shown in parentheses, these numbers are:It is possible that additional columns were present in the broken-off part of the tablet to the left of these columns. Conversion of these numbers from sexagesimal to decimal raises additional ambiguities, as the Babylonian sexagesimal notation did not specify the power of the initial digit of each number.
Interpretation
In each row, the number in the second column can be interpreted as the shortest side s of a right triangle, and the number in the third column can be interpreted as the hypotenuseHypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
d of the triangle. The number in the first column is either the fraction
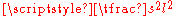 or
or 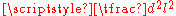 , where l denotes the longest side of the same right triangle. Scholars still differ, however, on how these numbers were generated.
, where l denotes the longest side of the same right triangle. Scholars still differ, however, on how these numbers were generated.argued for a number-theoretic
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
interpretation, pointing out that this table provides a list of (pairs of numbers from) Pythagorean triple
Pythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
s. For instance, line 11 of the table can be interpreted as describing a triangle with short side 3/4 and hypotenuse 5/4, forming the side:hypotenuse ratio of the familiar (3,4,5) right triangle
Special right triangles
A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45-45-90. This is called an "angle-based" right triangle...
. If p and q are two coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
numbers, then
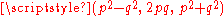 form a Pythagorean triple, and all Pythagorean triples can be formed in this way. For instance, line 11 can be generated by this formula with p = 1 and q = 1/2. As Neugebauer argues, each line of the tablet can be generated by a pair (p,q) that are both regular number
form a Pythagorean triple, and all Pythagorean triples can be formed in this way. For instance, line 11 can be generated by this formula with p = 1 and q = 1/2. As Neugebauer argues, each line of the tablet can be generated by a pair (p,q) that are both regular numberRegular number
Regular numbers are numbers that evenly divide powers of 60. As an example, 602 = 3600 = 48 × 75, so both 48 and 75 are divisors of a power of 60...
s, integer divisors of a power of 60. This property of p and q being regular leads to a denominator that is regular, and therefore to a finite sexagesimal representation for the fraction in the first column. Neugebauer's explanation is the one followed e.g. by . However, as points out, Neugebauer's theory fails to explain how the values of p and q were chosen: there are 92 pairs of coprime regular numbers up to 60, and only 15 entries in the table. In addition, it does not explain why the table entries are in the order they are listed in, nor what the numbers in the first column were used for.
discussed a possible trigonometric
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
explanation: the values of the first column can be interpreted as the squared cosine or tangent
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
(depending on the missing digit) of the angle opposite the short side of the right triangle described by each row, and the rows are sorted by these angles in roughly one-degree increments. However, Robson argues on linguistic grounds that this theory is "conceptually anachronistic": it depends on too many other ideas not present in the record of Babylonian mathematics from that time.
In contraposition with earlier explanations of the tablet,
claims that historical, cultural and linguistic evidence all reveal the tablet to be more likely "a list of regular
Regular number
Regular numbers are numbers that evenly divide powers of 60. As an example, 602 = 3600 = 48 × 75, so both 48 and 75 are divisors of a power of 60...
reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
pairs
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
." In 2003, the MAA awarded Robson with the Lester R. Ford Award for her work, stating it is "unlikely that the author of Plimpton 322 was either a professional or amateur mathematician. More likely he seems to have been a teacher and Plimpton 322 a set of exercises." Robson takes an approach that in modern terms would be characterized as algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic, though she describes it in concrete geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
terms and argues that the Babylonians would also have interpreted this approach geometrically.
Robson bases her interpretation on another tablet, YBC 6967, from roughly the same time and place. This tablet describes a method for solving what we would nowadays describe as quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
s of the form,
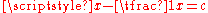 , by steps (described in geometric terms) in which the solver calculates a sequence of intermediate values v1 = c/2, v2 = v12, v3 = 1 + v2, and v4 = v31/2, from which one can calculate x = v4 + v1 and 1/x = v4 - v1.
, by steps (described in geometric terms) in which the solver calculates a sequence of intermediate values v1 = c/2, v2 = v12, v3 = 1 + v2, and v4 = v31/2, from which one can calculate x = v4 + v1 and 1/x = v4 - v1.Robson argues that the columns of Plimpton 322 can be interpreted as the following values, for regular number values of x and 1/x in numerical order:
-
- v3 in the first column,
- v1 = (x - 1/x)/2 in the second column, and
- v4 = (x + 1/x)/2 in the third column.
In this interpretation, x and 1/x would have appeared on the tablet in the broken-off portion to the left of the first column. For instance, row 11 of Plimpton 322 can be generated in this way for x = 2.
Thus, the tablet can be interpreted as giving a sequence of worked-out exercises of the type solved by the method from tablet YBC 6967, and reveals mathematical methods typical of scribal
Scribe
A scribe is a person who writes books or documents by hand as a profession and helps the city keep track of its records. The profession, previously found in all literate cultures in some form, lost most of its importance and status with the advent of printing...
schools of the time, and that it is written in a document format used by administrators in that period. Therefore, Robson argues that the author was likely a scribe, a bureaucrat in Larsa.
The repetitive mathematical set-up of the tablet, and of similar tablets such as BM 80209, would have been useful in allowing a teacher to set problems in the same format as each other but with different data. In short, Robson suggests that the tablet would likely have been used by a teacher as a problem set to assign to students.
Exhibitions
- "Before Pythagoras: The Culture of Old Babylonian Mathematics", Institute for the Study of the Ancient WorldInstitute for the Study of the Ancient WorldThe ' is a center for advanced scholarly research and graduate education that cultivates comparative and connective investigations of the ancient world from the western Mediterranean to China. It is a discrete entity within New York University, independent of any other school or department of the...
, New York UniversityNew York UniversityNew York University is a private, nonsectarian research university based in New York City. NYU's main campus is situated in the Greenwich Village section of Manhattan...
, November 12 - December 17, 2010. Includes photo and description of Plimpton 322).. Review of "Before Pythagoras" exhibit, mentioning controversy over Plimpton 322. - "Jewels in Her Crown: Treasures from the Special Collections of Columbia’s Libraries", Rare Book & Manuscript Library, Columbia UniversityColumbia UniversityColumbia University in the City of New York is a private, Ivy League university in Manhattan, New York City. Columbia is the oldest institution of higher learning in the state of New York, the fifth oldest in the United States, and one of the country's nine Colonial Colleges founded before the...
, October 8, 2004 - January 28, 2005. Photo and description of Item 158: Plimpton Cuneiform 322.

