Combinatorial principles
Encyclopedia
In proving results in combinatorics
several useful combinatorial rules or combinatorial principles are commonly recognized and used.
The rule of sum
, rule of product
, and inclusion-exclusion principle
are often used for enumerative
purposes. Bijective proof
s are utilized to demonstrate that two sets have the same number of elements. The pigeonhole principle often ascertains the existence of something or is used to determine the minimum or maximum number of something in a discrete
context. Many combinatorial identities arise from double counting
methods or the method of distinguished element
. Generating function
s and recurrence relation
s are powerful tools that can be used to manipulate sequences, and can describe if not resolve many combinatorial situations.

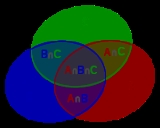
The inclusion-exclusion principle relates the size of the union of multiple sets, the size of each set, and the size of each possible intersection of the sets. The smallest example is when there are two sets: the number of elements in the union of A and B is equal to the sum of the number of elements in A and B, minus the number of elements in their intersection.
Generally, according to this principle, if A1, ..., An are finite sets, then
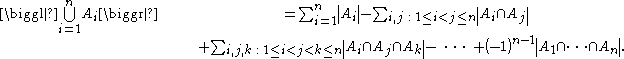

s for the terms of a sequence are more desired.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
several useful combinatorial rules or combinatorial principles are commonly recognized and used.
The rule of sum
Rule of sum
In combinatorics, the rule of sum or addition principle is a basic counting principle. Stated simply, it is the idea that if we have a ways of doing something and b ways of doing another thing and we can not do both at the same time, then there are a + b ways to choose one of the...
, rule of product
Rule of product
In combinatorics, the rule of product or multiplication principle is a basic counting principle...
, and inclusion-exclusion principle
Inclusion-exclusion principle
In combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
are often used for enumerative
Enumerative combinatorics
Enumerative combinatorics is an area of combinatorics that deals with the number of ways that certain patterns can be formed. Two examples of this type of problem are counting combinations and counting permutations...
purposes. Bijective proof
Bijective proof
In combinatorics, bijective proof is a proof technique that finds a bijective function f : A → B between two sets A and B, thus proving that they have the same number of elements, |A| = |B|. One place the technique is useful is where we wish to know the size of A, but can find no direct way of...
s are utilized to demonstrate that two sets have the same number of elements. The pigeonhole principle often ascertains the existence of something or is used to determine the minimum or maximum number of something in a discrete
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
context. Many combinatorial identities arise from double counting
Double counting (proof technique)
In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set...
methods or the method of distinguished element
Method of distinguished element
In enumerative combinatorial mathematics, identities are sometimes established by arguments that rely on singling out one "distinguished element" of a set.-Examples:...
. Generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
s and recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s are powerful tools that can be used to manipulate sequences, and can describe if not resolve many combinatorial situations.
Rule of sum
The rule of sum is an intuitive principle stating that if there are a possible outcomes for an event (or ways to do something) and b possible outcomes for another event (or ways to do another thing), and the two events cannot both occur (or the two things can't both be done), then there are a + b total possible outcomes for the events (or total possible ways to do one of the things). More formally, the sum of the sizes of two disjoint sets is equal to the size of their union.Rule of product
The rule of product is another intuitive principle stating that if there are a ways to do something and b ways to do another thing, then there are a · b ways to do both things.Inclusion-exclusion principle

The inclusion-exclusion principle relates the size of the union of multiple sets, the size of each set, and the size of each possible intersection of the sets. The smallest example is when there are two sets: the number of elements in the union of A and B is equal to the sum of the number of elements in A and B, minus the number of elements in their intersection.
Generally, according to this principle, if A1, ..., An are finite sets, then
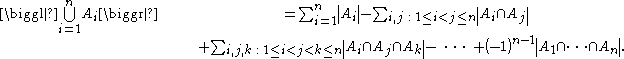
Bijective proof
Bijective proofs prove that two sets have the same number of elements by finding a bijective function (one-to-one correspondence) from one set to the other.Double counting
Double counting is a technique that equates two expressions that count the size of a set in two ways.Pigeonhole principle
The pigeonhole principle states that if a items are each put into one of b boxes, where a > b, then one of the boxes contains more than one item. Using this one can, for example, demonstrate the existence of some element in a set with some specific properties.Method of distinguished element
The method of distinguished element singles out a "distinguished element" of a set to prove some result.Generating function
Generating functions can be thought of as polynomials with infinitely many terms whose coefficients correspond to terms of a sequence. This new representation of the sequence opens up new methods for finding identities and closed forms pertaining to certain sequences. The (ordinary) generating function of a sequence an is
Recurrence relation
A recurrence relation defines each term of a sequence in terms of the preceding terms. Recurrence relations may lead to previously unknown properties of a sequence, but generally closed-form expressionClosed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
s for the terms of a sequence are more desired.

