Perrin number
Encyclopedia
In mathematics
, the Perrin numbers are defined by the recurrence relation
and
The sequence of Perrin numbers starts with
The number of different maximal independent set
s in an n-vertex cycle graph
is counted by the nth Perrin number.
(1878). In 1899, the same sequence was mentioned by
R. Perrin. The most extensive treatment of this sequence was given by Adams and Shanks (1982).
of the Perrin sequence is
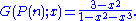
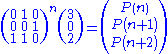
This equation has 3 roots; one real root p (known as the plastic number
) and two complex conjugate roots q and r. Given these three roots, the Perrin sequence analogue of the Fibonacci sequence Binet formula is
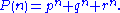
Since the magnitudes of the complex roots q and r are both less than 1, the powers of these roots approach 0 for large n. For large n the formula reduces to
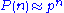
This formula can be used to quickly calculate values of the Perrin sequence for large n. The ratio of successive terms in the Perrin sequence approaches p, a.k.a. the plastic number
, which has a value of approximately 1.324718. This constant bears the same relationship to the Perrin sequence as the golden ratio
does to the Lucas sequence
. Similar connections exist also between p and the Padovan sequence
, between the golden ratio
and Fibonacci numbers, and between the silver ratio
and Pell number
s.
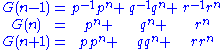
which gives us three linear equations with coefficients over the splitting field
of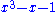
; by inverting a matrix we can solve for 
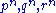and then we can raise them to the kth power and compute the sum.
Example magma
code:
P<x> := PolynomialRing(Rationals);
S<t> := SplittingField(x^3-x-1);
P2<y> := PolynomialRing(S);
p,q,r := Explode([r[1] : r in Roots(y^3-y-1)]);
Mi:=Matrix([[1/p,1/q,1/r],[1,1,1],[p,q,r]])^(-1);
T<u,v,w> := PolynomialRing(S,3);
v1 := ChangeRing(Mi,T) *Matrix([[u],[v],[w]]);
[p^i*v1[1,1]^3 + q^i*v1[2,1]^3 + r^i*v1[3,1]^3 : i in [-1..1]];
with the result that, if we have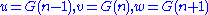
, then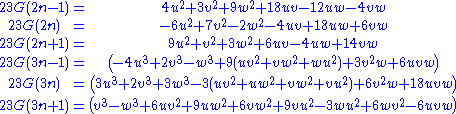
The number 23 here arises from the discriminant of the defining polynomial of the sequence.
This allows you to compute the nth Perrin number using integer arithmetic in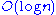
multiplies.
s n, n may still divide P(n). If n has this property, it is called a Perrin pseudoprime
.
The question of the existence of Perrin pseudoprimes was considered by Perrin himself, but it was not known whether they existed until Adams and Shanks (1982) discovered the smallest one, 271441 = 5212; the next-smallest is 904631 = 7 x 13 x 9941. There are seventeen of them less than a billion; Jon Grantham has proved that there are infinitely many Perrin pseudoprimes.
. The first few Perrin primes are:
E. W. Weisstein found a 32,147 digit probable Perrin prime P(263226) in May 2006.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Perrin numbers are defined by the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
- P(0) = 3, P(1) = 0, P(2) = 2,
and
- P(n) = P(n − 2) + P(n − 3) for n > 2.
The sequence of Perrin numbers starts with
- 3, 00 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, 2, 3, 2, 5, 5, 7, 1010 (number)10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
, 1212 (number)12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten...
, 1717 (number)17 is the natural number following 16 and preceding 18. It is prime.In spoken English, the numbers 17 and 70 are sometimes confused because they sound similar. When carefully enunciated, they differ in which syllable is stressed: 17 vs 70...
, 2222 (number)22 is the natural number following 21 and preceding 23.- In mathematics :Twenty-two is an even composite number, its proper divisors being 1, 2 and 11....
, 2929 (number)29 is the natural number following 28 and preceding 30.-In mathematics:It is the tenth prime number, and also the fourth primorial prime. It forms a twin prime pair with thirty-one, which is also a primorial prime. Twenty-nine is also the sixth Sophie Germain prime. It is also the sum of three...
, 3939 (number)39 is the natural number following 38 and preceding 40.- In mathematics :Thirty-nine is the sum of five consecutive primes and the sum of the first three powers of 3...
...
The number of different maximal independent set
Maximal independent set
In graph theory, a maximal independent set or maximal stable set is an independent set that is not a subset of any other independent set. That is, it is a set S such that every edge of the graph has at least one endpoint not in S and every vertex not in S has at least one neighbor in S...
s in an n-vertex cycle graph
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
is counted by the nth Perrin number.
History
This sequence was analyzed by Édouard LucasEdouard Lucas
François Édouard Anatole Lucas was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him.-Biography:...
(1878). In 1899, the same sequence was mentioned by
R. Perrin. The most extensive treatment of this sequence was given by Adams and Shanks (1982).
Generating function
The generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
of the Perrin sequence is
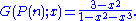
Matrix formula
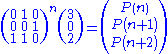
Binet-like formula
The Perrin sequence numbers can be written in terms of powers of the roots of the equationThis equation has 3 roots; one real root p (known as the plastic number
Plastic number
In mathematics, the plastic number ρ is a mathematical constant which is the unique real solution of the cubic equationx^3=x+1\, ....
) and two complex conjugate roots q and r. Given these three roots, the Perrin sequence analogue of the Fibonacci sequence Binet formula is
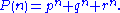
Since the magnitudes of the complex roots q and r are both less than 1, the powers of these roots approach 0 for large n. For large n the formula reduces to
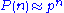
This formula can be used to quickly calculate values of the Perrin sequence for large n. The ratio of successive terms in the Perrin sequence approaches p, a.k.a. the plastic number
Plastic number
In mathematics, the plastic number ρ is a mathematical constant which is the unique real solution of the cubic equationx^3=x+1\, ....
, which has a value of approximately 1.324718. This constant bears the same relationship to the Perrin sequence as the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
does to the Lucas sequence
Lucas number
The Lucas numbers are an integer sequence named after the mathematician François Édouard Anatole Lucas , who studied both that sequence and the closely related Fibonacci numbers...
. Similar connections exist also between p and the Padovan sequence
Padovan sequence
The Padovan sequence is the sequence of integers P defined by the initial valuesP=P=P=1,and the recurrence relationP=P+P.The first few values of P are...
, between the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
and Fibonacci numbers, and between the silver ratio
Silver ratio
In mathematics, two quantities are in the silver ratio if the ratio between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational mathematical constant,...
and Pell number
Pell number
In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers...
s.
Multiplication formula
From the Binet formula, we can obtain a formula for G(kn) in terms of G(n−1), G(n) and G(n+1); we know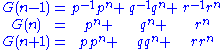which gives us three linear equations with coefficients over the splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of
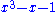; by inverting a matrix we can solve for 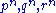and then we can raise them to the kth power and compute the sum.Example magma
Magma computer algebra system
Magma is a computer algebra system designed to solve problems in algebra, number theory, geometry and combinatorics. It is named after the algebraic structure magma...
code:
P<x> := PolynomialRing(Rationals);
S<t> := SplittingField(x^3-x-1);
P2<y> := PolynomialRing(S);
p,q,r := Explode([r[1] : r in Roots(y^3-y-1)]);
Mi:=Matrix([[1/p,1/q,1/r],[1,1,1],[p,q,r]])^(-1);
T<u,v,w> := PolynomialRing(S,3);
v1 := ChangeRing(Mi,T) *Matrix([[u],[v],[w]]);
[p^i*v1[1,1]^3 + q^i*v1[2,1]^3 + r^i*v1[3,1]^3 : i in [-1..1]];
with the result that, if we have
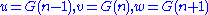, then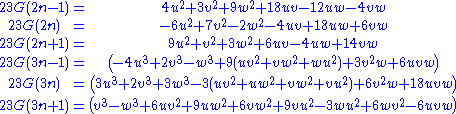The number 23 here arises from the discriminant of the defining polynomial of the sequence.
This allows you to compute the nth Perrin number using integer arithmetic in
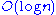multiplies.Perrin pseudoprimes
It has been proven that for all primes p, p divides P(p). However, the converse is not true: for some composite numberComposite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
s n, n may still divide P(n). If n has this property, it is called a Perrin pseudoprime
Pseudoprime
In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.- Definition :...
.
The question of the existence of Perrin pseudoprimes was considered by Perrin himself, but it was not known whether they existed until Adams and Shanks (1982) discovered the smallest one, 271441 = 5212; the next-smallest is 904631 = 7 x 13 x 9941. There are seventeen of them less than a billion; Jon Grantham has proved that there are infinitely many Perrin pseudoprimes.
Perrin primes
A Perrin prime is a Perrin number that is primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. The first few Perrin primes are:
- 2, 3, 5, 7, 17, 29, 277, 367, 853, 14197, 43721, 1442968193, 792606555396977, 187278659180417234321, 66241160488780141071579864797
E. W. Weisstein found a 32,147 digit probable Perrin prime P(263226) in May 2006.