
Pseudoprime
Encyclopedia
In number theory
, the Fermat pseudoprimes make up the most important class of pseudoprime
s that come from Fermat's little theorem
.
states that if p is prime and a is coprime
to p, then ap−1 − 1 is divisible
by p. If a composite integer x is coprime to an integer a > 1 and x divides ax−1 − 1, then x is called a Fermat pseudoprime to base a. In other words, a composite integer is a Fermat pseudoprime to base a if it successfully passes Fermat primality test
for the base a.
The smallest base-2 Fermat pseudoprime is 341. It is not a prime, since it equals 11·31, but it satisfies Fermat's little theorem: 2340 ≡ 1 (mod 341) and thus passes
Fermat primality test
for the base 2.
Pseudoprimes to base 2 are sometimes called Poulet numbers, Sarrus numbers, or Fermatians .
An integer x that is a Fermat pseudoprime for all values of a that are coprime to x is called a Carmichael number.
Every odd number q satisfies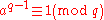 for
for 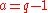 . This trivial case is excluded in the definition of a Fermat pseudoprime given by Crandall
. This trivial case is excluded in the definition of a Fermat pseudoprime given by Crandall
and Pomerance
:
This stronger definition excludes every power of three (9, 27, 81, 243, ...), and many even integers from the base-2 Fermat pseudoprimes.
A Poulet number all of whose divisors d divide 2d − 2 is called a super-Poulet number. There are infinitely many Poulet numbers which are not super-Poulet Numbers.
s or Euler–Jacobi pseudoprimes, for which there are no analogues of Carmichael numbers. This leads to probabilistic algorithm
s such as the Solovay–Strassen primality test and the Miller–Rabin primality test, which produce what are known as industrial-grade primes. Industrial-grade primes are integers for which primality has not been "certified" (i.e. rigorously proven), but have undergone a test such as the Miller–Rabin test which has nonzero, but arbitrarily low, probability of failure.
algorithms such as RSA require the ability to quickly find large primes. The usual algorithm to generate prime numbers is to generate random odd numbers and test
them for primality. However, deterministic
primality tests are slow. If the user is willing to tolerate an arbitrarily small chance that the number found is not a prime number but a pseudoprime, it is possible to use the much faster and simpler Fermat primality test
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Fermat pseudoprimes make up the most important class of pseudoprime
Pseudoprime
In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.- Definition :...
s that come from Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
.
Definition
Fermat's little theoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
states that if p is prime and a is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to p, then ap−1 − 1 is divisible
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
by p. If a composite integer x is coprime to an integer a > 1 and x divides ax−1 − 1, then x is called a Fermat pseudoprime to base a. In other words, a composite integer is a Fermat pseudoprime to base a if it successfully passes Fermat primality test
Fermat primality test
The Fermat primality test is a probabilistic test to determine if a number is probable prime.-Concept:Fermat's little theorem states that if p is prime and 1 \le a...
for the base a.
The smallest base-2 Fermat pseudoprime is 341. It is not a prime, since it equals 11·31, but it satisfies Fermat's little theorem: 2340 ≡ 1 (mod 341) and thus passes
Fermat primality test
Fermat primality test
The Fermat primality test is a probabilistic test to determine if a number is probable prime.-Concept:Fermat's little theorem states that if p is prime and 1 \le a...
for the base 2.
Pseudoprimes to base 2 are sometimes called Poulet numbers, Sarrus numbers, or Fermatians .
An integer x that is a Fermat pseudoprime for all values of a that are coprime to x is called a Carmichael number.
Variations
Some sources use variations of the definition, for example to only allow odd numbers to be pseudoprimes.Every odd number q satisfies
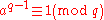 for
for 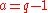 . This trivial case is excluded in the definition of a Fermat pseudoprime given by Crandall
. This trivial case is excluded in the definition of a Fermat pseudoprime given by CrandallRichard Crandall
Richard E. Crandall is an American Physicist and computer scientist who has made contributions to computational number theory.He is most notable for the development of the irrational base discrete weighted transform, an important method of finding very large primes. He has, at various times, been...
and Pomerance
Carl Pomerance
Carl Bernard Pomerance is a well-known number theorist. He attended college at Brown University and later received his Ph.D. from Harvard University in 1972 with a dissertation proving that any odd perfect number has at least 7 distinct prime factors. He immediately joined the faculty at the...
:
- A composite number q is a Fermat pseudoprime to a base a, if
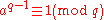 and
and 
This stronger definition excludes every power of three (9, 27, 81, 243, ...), and many even integers from the base-2 Fermat pseudoprimes.
Distribution
There are infinitely many pseudoprimes to a given base (in fact, infinitely many Carmichael numbers), but they are rather rare. There are only three pseudo-primes to base 2 below 1000, and below a million there are only 245. Starting at 17·257, the product of consecutive Fermat numbers is a base-2 pseudo-prime.Factorizations
The factorizations of the 60 Poulet numbers up to 60787, including 13 Carmichael numbers (in bold), are in the below table.
|
|
|
|
A Poulet number all of whose divisors d divide 2d − 2 is called a super-Poulet number. There are infinitely many Poulet numbers which are not super-Poulet Numbers.
Smallest Fermat pseudoprimes
The smallest pseudoprime for each base a ≤ 200 is given in the following table; the colors mark the number of prime factors. Unlike in the definition at the start of the article, pseudoprimes below a are excluded in the table.| a | smallest p-p | a | smallest p-p | a | smallest p-p | a | smallest p-p |
|---|---|---|---|---|---|---|---|
| 51 | 65 = 5 · 13 | 101 | 175 = 5² · 7 | 151 | 175 = 5² · 7 | ||
| 2 | 341 = 11 · 31 | 52 | 85 = 5 · 17 | 102 | 133 = 7 · 19 | 152 | 153 = 3² · 17 |
| 3 | 91 = 7 · 13 | 53 | 65 = 5 · 13 | 103 | 133 = 7 · 19 | 153 | 209 = 11 · 19 |
| 4 | 15 = 3 · 5 | 54 | 55 = 5 · 11 | 104 | 105 = 3 · 5 · 7 | 154 | 155 = 5 · 31 |
| 5 | 124 = 2² · 31 | 55 | 63 = 3² · 7 | 105 | 451 = 11 · 41 | 155 | 231 = 3 · 7 · 11 |
| 6 | 35 = 5 · 7 | 56 | 57 = 3 · 19 | 106 | 133 = 7 · 19 | 156 | 217 = 7 · 31 |
| 7 | 25 = 5² | 57 | 65 = 5 · 13 | 107 | 133 = 7 · 19 | 157 | 186 = 2 · 3 · 31 |
| 8 | 9 = 3² | 58 | 133 = 7 · 19 | 108 | 341 = 11 · 31 | 158 | 159 = 3 · 53 |
| 9 | 28 = 2² · 7 | 59 | 87 = 3 · 29 | 109 | 117 = 3² · 13 | 159 | 247 = 13 · 19 |
| 10 | 33 = 3 · 11 | 60 | 341 = 11 · 31 | 110 | 111 = 3 · 37 | 160 | 161 = 7 · 23 |
| 11 | 15 = 3 · 5 | 61 | 91 = 7 · 13 | 111 | 190 = 2 · 5 · 19 | 161 | 190=2 · 5 · 19 |
| 12 | 65 = 5 · 13 | 62 | 63 = 3² · 7 | 112 | 121 = 11² | 162 | 481 = 13 · 37 |
| 13 | 21 = 3 · 7 | 63 | 341 = 11 · 31 | 113 | 133 = 7 · 19 | 163 | 186 = 2 · 3 · 31 |
| 14 | 15 = 3 · 5 | 64 | 65 = 5 · 13 | 114 | 115 = 5 · 23 | 164 | 165 = 3 · 5 · 11 |
| 15 | 341 = 11 · 13 | 65 | 112 = 24 · 7 | 115 | 133 = 7 · 19 | 165 | 172 = 2² · 43 |
| 16 | 51 = 3 · 17 | 66 | 91 = 7 · 13 | 116 | 117 = 3² · 13 | 166 | 301 = 7 · 43 |
| 17 | 45 = 3² · 5 | 67 | 85 = 5 · 17 | 117 | 145 = 5 · 29 | 167 | 231 = 3 · 7 · 11 |
| 18 | 25 = 5² | 68 | 69 = 3 · 23 | 118 | 119 = 7 · 17 | 168 | 169 = 13² |
| 19 | 45 = 3² · 5 | 69 | 85 = 5 · 17 | 119 | 177 = 3 · 59 | 169 | 231 = 3 · 7 · 11 |
| 20 | 21 = 3 · 7 | 70 | 169 = 13² | 120 | 121 = 11² | 170 | 171 = 3² · 19 |
| 21 | 55 = 5 · 11 | 71 | 105 = 3 · 5 · 7 | 121 | 133 = 7 · 19 | 171 | 215 = 5 · 43 |
| 22 | 69 = 3 · 23 | 72 | 85 = 5 · 17 | 122 | 123 = 3 · 41 | 172 | 247 = 13 · 19 |
| 23 | 33 = 3 · 11 | 73 | 111 = 3 · 37 | 123 | 217 = 7 · 31 | 173 | 205 = 5 · 41 |
| 24 | 25 = 5² | 74 | 75 = 3 · 5² | 124 | 125 = 5³ | 174 | 175 = 5² · 7 |
| 25 | 28 = 2² · 7 | 75 | 91 = 7 · 13 | 125 | 133 = 7 · 19 | 175 | 319 = 11 · 19 |
| 26 | 27 = 3³ | 76 | 77 = 7 · 11 | 126 | 247 = 13 · 19 | 176 | 177 = 3 · 59 |
| 27 | 65 = 5 · 13 | 77 | 247 = 13 · 19 | 127 | 153 = 3² · 17 | 177 | 196 = 2² · 7² |
| 28 | 45 = 3² · 5 | 78 | 341 = 11 · 31 | 128 | 129 = 3 · 43 | 178 | 247 = 13 · 19 |
| 29 | 35 = 5 · 7 | 79 | 91 = 7 · 13 | 129 | 217 = 7 · 31 | 179 | 185 = 5 · 37 |
| 30 | 49 = 7² | 80 | 81 = 34 | 130 | 217 = 7 · 31 | 180 | 217 = 7 · 31 |
| 31 | 49 = 7² | 81 | 85 = 5 · 17 | 131 | 143 = 11 · 13 | 181 | 195 = 3 · 5 · 13 |
| 32 | 33 = 3 · 11 | 82 | 91 = 7 · 13 | 132 | 133 = 7 · 19 | 182 | 183 = 3 · 61 |
| 33 | 85 = 5 · 17 | 83 | 105 = 3 · 5 · 7 | 133 | 145 = 5 · 29 | 183 | 221 = 13 · 17 |
| 34 | 35 = 5 · 7 | 84 | 85 = 5 · 17 | 134 | 135 = 3³ · 5 | 184 | 185 = 5 · 37 |
| 35 | 51 = 3 · 17 | 85 | 129 = 3 · 43 | 135 | 221 = 13 · 17 | 185 | 217 = 7 · 31 |
| 36 | 91 = 7 · 13 | 86 | 87 = 3 · 29 | 136 | 265 = 5 · 53 | 186 | 187 = 11 · 17 |
| 37 | 45 = 3² · 5 | 87 | 91 = 7 · 13 | 137 | 148 = 2² · 37 | 187 | 217 = 7 · 31 |
| 38 | 39 = 3 · 13 | 88 | 91 = 7 · 13 | 138 | 259 = 7 · 37 | 188 | 189 = 3³ · 7 |
| 39 | 95 = 5 · 19 | 89 | 99 = 3² · 11 | 139 | 161 = 7 · 23 | 189 | 235 = 5 · 47 |
| 40 | 91 = 7 · 13 | 90 | 91 = 7 · 13 | 140 | 141 = 3 · 47 | 190 | 231 = 3 · 7 · 11 |
| 41 | 105 = 3 · 5 · 7 | 91 | 115 = 5 · 23 | 141 | 355 = 5 · 71 | 191 | 217 = 7 · 31 |
| 42 | 205 = 5 · 41 | 92 | 93 = 3 · 31 | 142 | 143 = 11 · 13 | 192 | 217 = 7 · 31 |
| 43 | 77 = 7 · 11 | 93 | 301 = 7 · 43 | 143 | 213 = 3 · 71 | 193 | 276 = 2² · 3 · 23 |
| 44 | 45 = 3² · 5 | 94 | 95 = 5 · 19 | 144 | 145 = 5 · 29 | 194 | 195 = 3 · 5 · 13 |
| 45 | 76 = 2² · 19 | 95 | 141 = 3 · 47 | 145 | 153 = 3² · 17 | 195 | 259 = 7 · 37 |
| 46 | 133 = 7 · 19 | 96 | 133 = 7 · 19 | 146 | 147 = 3 · 7² | 196 | 205 = 5 · 41 |
| 47 | 65 = 5 · 13 | 97 | 105 = 3 · 5 · 7 | 147 | 169 = 13² | 197 | 231 = 3 · 7 · 11 |
| 48 | 49 = 7² | 98 | 99 = 3² · 11 | 148 | 231 = 3 · 7 · 11 | 198 | 247 = 13 · 19 |
| 49 | 66 = 2 · 3 · 11 | 99 | 145 = 5 · 29 | 149 | 175 = 5² · 7 | 199 | 225 = 3² · 5² |
| 50 | 51 = 3 · 17 | 100 | 153 = 3² · 17 | 150 | 169 = 13² | 200 | 201 = 3 · 67 |
Euler–Jacobi pseudoprimes
Another approach is to use more refined notions of pseudoprimality, e.g. strong pseudoprimeStrong pseudoprime
In number theory, a strong pseudoprime is a composite number that passes a primality test. All primes pass this test, but a small fraction of composites pass as well, making them "false primes"...
s or Euler–Jacobi pseudoprimes, for which there are no analogues of Carmichael numbers. This leads to probabilistic algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
s such as the Solovay–Strassen primality test and the Miller–Rabin primality test, which produce what are known as industrial-grade primes. Industrial-grade primes are integers for which primality has not been "certified" (i.e. rigorously proven), but have undergone a test such as the Miller–Rabin test which has nonzero, but arbitrarily low, probability of failure.
Applications
The rarity of such pseudoprimes has important practical implications. For example, public-key cryptographyPublic-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
algorithms such as RSA require the ability to quickly find large primes. The usual algorithm to generate prime numbers is to generate random odd numbers and test
Primality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
them for primality. However, deterministic
Deterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
primality tests are slow. If the user is willing to tolerate an arbitrarily small chance that the number found is not a prime number but a pseudoprime, it is possible to use the much faster and simpler Fermat primality test
Fermat primality test
The Fermat primality test is a probabilistic test to determine if a number is probable prime.-Concept:Fermat's little theorem states that if p is prime and 1 \le a...
.
External links
- W. F. Galway, Database of Base-2 Pseudoprimes up to 10^15 (including Strong Pseudoprimes and Carmichael numbers)

