Padovan sequence
Encyclopedia
The Padovan sequence is the sequence
of integer
s P(n) defined by the initial values

and the recurrence relation

The first few values of P(n) are
 The Padovan sequence is named after Richard Padovan
The Padovan sequence is named after Richard Padovan
who attributed its discovery to Dutch
architect Hans van der Laan in his 1994 essay Dom. Hans van der Laan : Modern Primitive. The sequence was described by Ian Stewart
in his Scientific American
column Mathematical Recreations in June 1996.
The above definition is the one given by Ian Stewart and by MathWorld
. Other sources may start the sequence at a different place, in which case some of the identities in this article must be adjusted with appropriate offsets.
the Padovan sequence also satisfies the recurrence relation
Starting from this, the defining recurrence and other recurrences as they are discovered,
one can create an infinite number of further recurrences by repeatedly replacing by
by 
The Perrin sequence satisfies the same recurrence relations as the Padovan sequence, although it has different initial values. This is a property of recurrence relations.
The Perrin sequence can be obtained from the Padovan sequence by the
following formula:


Starting with m=-1 and working backwards, we extend P(m) to negative indices:

Sums of alternate terms, sums of every third term and sums of every fifth term are also related to other terms in the sequence:






Sums involving products of terms in the Padovan sequence satisfy the following identities:




The Padovan sequence is related to sums of binomial coefficient
s by the following identity:

For example, for k = 12, the values for the pair (m, n) with 2m + n = 12 which give non-zero binomial coefficients are (6, 0), (5, 2) and (4, 4), and:


This equation has 3 roots; one real root p (known as the plastic number
) and two complex conjugate roots q and r. Given these three roots, the Padovan sequence can be expressed by a formula involving p,q and r:

where a, b and c are constants.
Since the magnitudes of the complex roots q and r are both less than 1 (and hence p is a Pisot–Vijayaraghavan number), the powers of these roots approach 0 for large n, and tends to zero.
tends to zero.
For all , P(n) is the integer closest to
, P(n) is the integer closest to  ,
,
where s = p/a = 1.0453567932525329623... is the only real root of s3 − 2s2 + 23s − 23 = 0. The ratio of successive terms in the Padovan sequence approaches p, which has a value of approximately 1.324718. This constant bears the same relationship to the Padovan sequence
and the Perrin sequence as the golden ratio
does to the Fibonacci sequence.
of the Padovan sequence is

This can be used to prove identities involving products of the Padovan sequence with geometric terms, such as:

called the Fibonacci polynomials, the Padovan sequence numbers can be generalized to
yield the Padovan polynomials.
. The first few Padovan primes are
then this Lindenmayer system or L-system
produces the following sequence of strings:
and if we count the length of each string, we obtain the Padovan sequence of numbers:
Also, if you count the number of As, Bs and Cs in each string, then for the nth
string, you have P(n − 5) As, P(n − 3) Bs and P(n − 4) Cs. The count of BB pairs, AA pairs
and CC pairs are also Padovan numbers.
This is the Padovan cuboid spiral
. Successive sides of this spiral have lengths that are
the Padovan sequence numbers multiplied by the square root of 2.
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s P(n) defined by the initial values

and the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....

The first few values of P(n) are
- 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265, ...

Richard Padovan
Richard Padovan is an architect, author, translator and lecturer. In the 1950s he studied at the Architectural Association School of Architecture; he has practised architecture in several European countries, and taught at the University of Bath...
who attributed its discovery to Dutch
Netherlands
The Netherlands is a constituent country of the Kingdom of the Netherlands, located mainly in North-West Europe and with several islands in the Caribbean. Mainland Netherlands borders the North Sea to the north and west, Belgium to the south, and Germany to the east, and shares maritime borders...
architect Hans van der Laan in his 1994 essay Dom. Hans van der Laan : Modern Primitive. The sequence was described by Ian Stewart
Ian Stewart (mathematician)
Ian Nicholas Stewart FRS is a professor of mathematics at the University of Warwick, England, and a widely known popular-science and science-fiction writer. He is the first recipient of the , awarded jointly by the LMS and the IMA for his work on promoting mathematics.-Biography:Stewart was born...
in his Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
column Mathematical Recreations in June 1996.
The above definition is the one given by Ian Stewart and by MathWorld
MathWorld
MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
. Other sources may start the sequence at a different place, in which case some of the identities in this article must be adjusted with appropriate offsets.
Recurrence relations
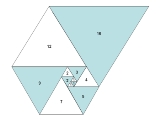
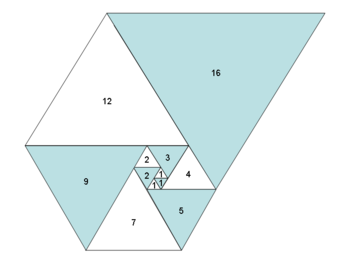
In the spiral, each triangle shares a side with two others giving a visual proof thatthe Padovan sequence also satisfies the recurrence relation

Starting from this, the defining recurrence and other recurrences as they are discovered,
one can create an infinite number of further recurrences by repeatedly replacing
 by
by 
The Perrin sequence satisfies the same recurrence relations as the Padovan sequence, although it has different initial values. This is a property of recurrence relations.
The Perrin sequence can be obtained from the Padovan sequence by the
following formula:

Extension to negative parameters
As with any sequence defined by a recurrence relation, Padovan numers P(m) for m<0 can be defined by rewriting the recurrence relation as
Starting with m=-1 and working backwards, we extend P(m) to negative indices:
| P−20 | P−19 | P−18 | P−17 | P−16 | P−15 | P−14 | P−13 | P−12 | P−11 | P-10 | P-9 | P-8 | P-7 | P-6 | P-5 | P-4 | P-3 | P-2 | P-1 | P0 | P1 | P2 |
| 7 | -7 | 4 | 0 | −3 | 4 | −3 | 1 | 1 | -2 | 2 | -1 | 0 | 1 | -1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
Sums of terms
The sum of the first n terms in the Padovan sequence is 2 less than P(n + 5) i.e.
Sums of alternate terms, sums of every third term and sums of every fifth term are also related to other terms in the sequence:






Sums involving products of terms in the Padovan sequence satisfy the following identities:



Other identities
The Padovan sequence also satisfies the identity
The Padovan sequence is related to sums of binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s by the following identity:

For example, for k = 12, the values for the pair (m, n) with 2m + n = 12 which give non-zero binomial coefficients are (6, 0), (5, 2) and (4, 4), and:

Binet-like formula
The Padovan sequence numbers can be written in terms of powers of the roots of the equation
This equation has 3 roots; one real root p (known as the plastic number
Plastic number
In mathematics, the plastic number ρ is a mathematical constant which is the unique real solution of the cubic equationx^3=x+1\, ....
) and two complex conjugate roots q and r. Given these three roots, the Padovan sequence can be expressed by a formula involving p,q and r:

where a, b and c are constants.
Since the magnitudes of the complex roots q and r are both less than 1 (and hence p is a Pisot–Vijayaraghavan number), the powers of these roots approach 0 for large n, and
 tends to zero.
tends to zero.For all
 , P(n) is the integer closest to
, P(n) is the integer closest to  ,
,where s = p/a = 1.0453567932525329623... is the only real root of s3 − 2s2 + 23s − 23 = 0. The ratio of successive terms in the Padovan sequence approaches p, which has a value of approximately 1.324718. This constant bears the same relationship to the Padovan sequence
and the Perrin sequence as the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
does to the Fibonacci sequence.
Combinatorial interpretations
- P(n) is the number of ways of writing n + 2 as an ordered sum in which each term is either 2 or 3 (i.e. the number of compositionsComposition (number theory)In mathematics, a composition of an integer n is a way of writing n as the sum of a sequence of positive integers. Two sequences that differ in the order of their terms define different compositions of their sum, while they are considered to define the same partition of that number. Any integer...
of n + 2 in which each term is either 2 or 3). For example, P(6) = 4, and there are 4 ways to write 8 as an ordered sum of 2s and 3s:
-
- 2 + 2 + 2 + 2 ; 2 + 3 + 3 ; 3 + 2 + 3 ; 3 + 3 + 2
- The number of ways of writing n as an ordered sum in which no term is 2 is P(2n − 2). For example, P(6) = 4, and there are 4 ways to write 4 as an ordered sum in which no term is 2:
-
- 4 ; 1 + 3 ; 3 + 1 ; 1 + 1 + 1 + 1
- The number of ways of writing n as a palindromic ordered sum in which no term is 2 is P(n). For example, P(6) = 4, and there are 4 ways to write 6 as a palindromic ordered sum in which no term is 2:
-
- 6 ; 3 + 3 ; 1 + 4 + 1 ; 1 + 1 + 1 + 1 + 1 + 1
- The number of ways of writing n as an ordered sum in which each term is congruent to 2 mod 3 is equal to P(n − 4). For example, P(6) = 4, and there are 4 ways to write 10 as an ordered sum in which each term is congruent to 2 mod 3:
-
- 8 + 2 ; 2 + 8 ; 5 + 5 ; 2 + 2 + 2 + 2 + 2
Generating function
The generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
of the Padovan sequence is

This can be used to prove identities involving products of the Padovan sequence with geometric terms, such as:

Generalizations
In a similar way to the Fibonacci numbers that can be generalized to a set of polynomialscalled the Fibonacci polynomials, the Padovan sequence numbers can be generalized to
yield the Padovan polynomials.
Padovan prime
A Padovan prime is P(n) that is primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. The first few Padovan primes are
- 2, 3, 5, 7, 37, 151, 3329, 23833, ....
Padovan L-system
If we define the following simple grammar:- variables : A B C
- constants : none
- start : A
- rules : (A → B), (B → C), (C → AB)
then this Lindenmayer system or L-system
L-system
An L-system or Lindenmayer system is a parallel rewriting system, namely a variant of a formal grammar, most famously used to model the growth processes of plant development, but also able to model the morphology of a variety of organisms...
produces the following sequence of strings:
- n = 0 : A
- n = 1 : B
- n = 2 : C
- n = 3 : AB
- n = 4 : BC
- n = 5 : CAB
- n = 6 : ABBC
- n = 7 : BCCAB
- n = 8 : CABABBC
and if we count the length of each string, we obtain the Padovan sequence of numbers:
- 1 1 1 2 2 3 4 5 ...
Also, if you count the number of As, Bs and Cs in each string, then for the nth
string, you have P(n − 5) As, P(n − 3) Bs and P(n − 4) Cs. The count of BB pairs, AA pairs
and CC pairs are also Padovan numbers.
Padovan Cuboid Spiral
A spiral can be formed based on connecting the corners of a set of 3 dimensional cuboids.This is the Padovan cuboid spiral
Padovan cuboid spiral
In mathematics the Padovan cuboid spiral is the spiral created by joining the diagonals of faces of successive cuboids added to a unit cube. The cuboids are added sequentially so that the resulting cuboid has dimensions that are successive Padovan numbers....
. Successive sides of this spiral have lengths that are
the Padovan sequence numbers multiplied by the square root of 2.
External links
- Padovan sequence: in the OEIS
- Dom Hans Van Der Laan And The Plastic Number by Richard Padovan
- Tales of a Neglected Number by Ian Stewart
- A Padovan Sequence Calculator can be found here.

