Perfect power
Encyclopedia
In mathematics
, a perfect power is a positive integer
that can be expressed as an integer power
of another positive integer. More formally, n is a perfect power if there exist natural number
s m > 1, and k > 1 such that mk = n. In this case, n may be called a perfect kth power. If k = 2 or k = 3, then n is called a perfect square
or perfect cube, respectively. Sometimes 1 is also considered a perfect power (1k = 1 for any k).
of perfect powers can be generated by iterating through the possible values for m and k. The first few ascending perfect powers in numerical order (showing duplicate powers) are :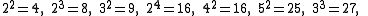
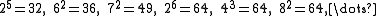
The sum
of the reciprocals of the perfect powers (including duplicates) is 1: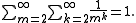
which can be proved as follows: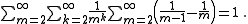
The first perfect powers without duplicates are :, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, 128, 144, 169, 196, 216, 225, 243, 256, 289, 324, 343, 361, 400, 441, 484, ...
The sum of the reciprocals of the perfect powers p without duplicates is:
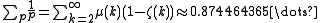
where μ(k) is the Möbius function
and ζ(k) is the Riemann zeta function.
According to Euler
, Goldbach
showed (in a now lost letter) that the sum of 1/(p−1) over the set of perfect powers p, excluding 1 and excluding duplicates, is 1:
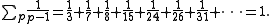
This is sometimes known as the Goldbach-Euler theorem.
The constant concatenating "0." with the base 10 representations of perfect powers in order will be irrational number.
. One of the simplest such methods is to consider all possible values for k across each of the divisor
s of n, up to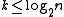
. So if the divisors of 
are 
then one of the values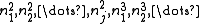 
must be equal to n if n is indeed a perfect power.
This method can immediately be simplified by instead considering only prime
values of k. This is because if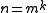
for a composite
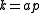where p is prime, then this can simply be rewritten as 
. Because of this result, the minimal value of k must necessarily be prime.
proved that the only pair of consecutive perfect powers is 23 = 8 and 32 = 9, thus proving Catalan's conjecture.
Pillai's conjecture states that for any given positive integer k there are only a finite number of pairs of perfect powers whose difference is k. This is an unsolved problem.
Define the following function on the range of positive integers: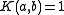
where a = 1 or a = b
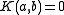where b > a
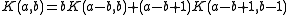elsewhere
This function generates the following output:
Also define the following function on the range of positive integers:
(This is very closely related to the Binomial Theorem and Pascal's Triangle)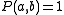
where a = 1 or b = 1
elsewhere
The table this generates can be seen as pascal's triangle fallen over to the left, so that what were rows on Pascal's triangle have become diagonal series in the table.
It can then be stated that: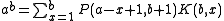
Example: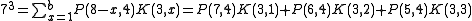
Expanding P(7,4)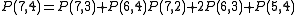
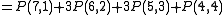
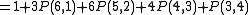
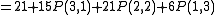
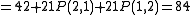
Or you can look up the values on the table and get P(6,4) = 56, and P(5,4) = 35.
By definition, K(3,1) = 1. Expanding K(3,2)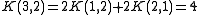
By definition, K(3,3) = 1.
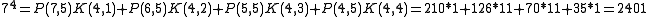
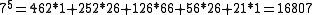
This calculation method can be used for all integer power calculations, as negative integers act the same way, simply applying he negative if the exponent is odd.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a perfect power is a positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
that can be expressed as an integer power
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of another positive integer. More formally, n is a perfect power if there exist natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s m > 1, and k > 1 such that mk = n. In this case, n may be called a perfect kth power. If k = 2 or k = 3, then n is called a perfect square
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
or perfect cube, respectively. Sometimes 1 is also considered a perfect power (1k = 1 for any k).
Examples and sums
A sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of perfect powers can be generated by iterating through the possible values for m and k. The first few ascending perfect powers in numerical order (showing duplicate powers) are :
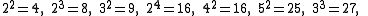
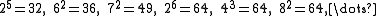
The sum
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of the reciprocals of the perfect powers (including duplicates) is 1:
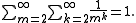
which can be proved as follows:
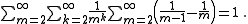
The first perfect powers without duplicates are :, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, 128, 144, 169, 196, 216, 225, 243, 256, 289, 324, 343, 361, 400, 441, 484, ...
The sum of the reciprocals of the perfect powers p without duplicates is:
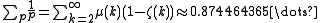
where μ(k) is the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
and ζ(k) is the Riemann zeta function.
According to Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, Goldbach
Christian Goldbach
Christian Goldbach was a German mathematician who also studied law. He is remembered today for Goldbach's conjecture.-Biography:...
showed (in a now lost letter) that the sum of 1/(p−1) over the set of perfect powers p, excluding 1 and excluding duplicates, is 1:
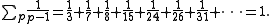
This is sometimes known as the Goldbach-Euler theorem.
The constant concatenating "0." with the base 10 representations of perfect powers in order will be irrational number.
Detecting perfect powers
Detecting whether or not a given natural number n is a perfect power may be accomplished in many different ways, with varying levels of complexityComputational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
. One of the simplest such methods is to consider all possible values for k across each of the divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s of n, up to
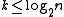. So if the divisors of are then one of the values 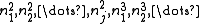must be equal to n if n is indeed a perfect power.This method can immediately be simplified by instead considering only prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
values of k. This is because if
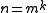for a compositeComposite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
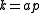where p is prime, then this can simply be rewritten as . Because of this result, the minimal value of k must necessarily be prime.Gaps between perfect powers
In 2002 Romanian mathematician Preda MihăilescuPreda Mihailescu
Preda V. Mihăilescu is a Romanian mathematician, best known for his proof of Catalan's conjecture.Born in Bucharest, he is the brother of Vintilă Mihăilescu. After leaving Romania in 1973, he settled in Switzerland. He studied mathematics and computer science in Zürich, receiving his Ph.D. from...
proved that the only pair of consecutive perfect powers is 23 = 8 and 32 = 9, thus proving Catalan's conjecture.
Pillai's conjecture states that for any given positive integer k there are only a finite number of pairs of perfect powers whose difference is k. This is an unsolved problem.
Calculation by Recursion for positive integers
This being an alternate way to calculate perfect powers has yet to be found useful. It is based on the observation that the difference between ab and (a+1)b where a > b may not be constant, but if you take the difference of successive differences, b times, there is a constant b! factor. For example, 94 = 6561, and 104 is 10000. the difference is 3439. The difference between 84 and 94 is 2465, meaning the difference of differences is 974. A step further and you have 204. One step further, and you have 24, which is equal to 4!. One step further and collating this 'key' row from progressively larger exponents yields a triangle similar to Pascal's, but with a differing formula for generation. A part of this table is shown below:Define the following function on the range of positive integers:
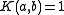where a = 1 or a = b 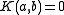where b > a 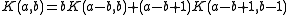elsewhereThis function generates the following output:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 0 | 0 | 0 |
| 3 | 1 | 4 | 1 | 0 | 0 | 0 |
| 4 | 1 | 11 | 11 | 1 | 0 | 0 |
| 5 | 1 | 26 | 66 | 26 | 1 | 0 |
| 6 | 1 | 57 | 302 | 302 | 57 | 1 |
Also define the following function on the range of positive integers:
(This is very closely related to the Binomial Theorem and Pascal's Triangle)
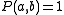where a = 1 or b = 1 elsewhereThe table this generates can be seen as pascal's triangle fallen over to the left, so that what were rows on Pascal's triangle have become diagonal series in the table.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 |
| 4 | 1 | 4 | 10 | 20 | 35 | 56 | 84 | 120 |
| 5 | 1 | 5 | 15 | 35 | 70 | 126 | 210 | 330 |
| 6 | 1 | 6 | 21 | 56 | 126 | 252 | 462 | 792 |
| 7 | 1 | 7 | 28 | 84 | 210 | 462 | 924 | 1716 |
| 8 | 1 | 8 | 36 | 120 | 330 | 792 | 1716 | 3432 |
It can then be stated that:
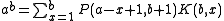
Example:
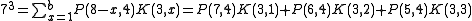
Expanding P(7,4)
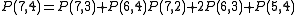
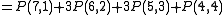
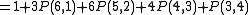
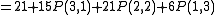
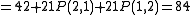
Or you can look up the values on the table and get P(6,4) = 56, and P(5,4) = 35.
By definition, K(3,1) = 1. Expanding K(3,2)
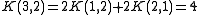
By definition, K(3,3) = 1.
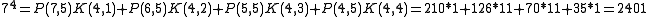
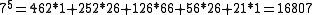
This calculation method can be used for all integer power calculations, as negative integers act the same way, simply applying he negative if the exponent is odd.