Particular values of the Gamma function
Encyclopedia
The Gamma function
is an important special function in mathematics
. Its particular values can be expressed in closed form for integer
and half-integer
arguments, but no simple expressions are known for the values at rational
points in general. Other fractional arguments can be approximated through efficient infinite products, infinite series, and recurrence relations.
, that is,
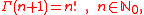
and hence
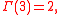
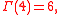
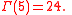
For non-positive integers, the Gamma function is not defined.
For positive half-integers, the function values are given exactly by
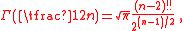
or equivalently, for non-negative integer values of n:
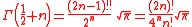
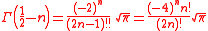
where n!! denotes the double factorial. In particular,
and by means of the reflection formula
,
where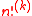
denotes the k:th multifactorial of n. By exploiting such functional relations, the Gamma function of any rational argument 
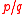can be expressed in closed algebraic form in terms of 
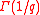. However, no closed expressions are known for the numbers 
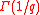where q > 2. Numerically,
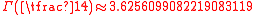
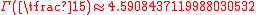
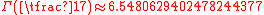
It is unknown whether these constants are transcendental
in general, but
and 
were shown to be transcendental by Chudnovsky
.
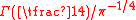has also long been known to be transcendental, and Yuri Nesterenko
proved in 1996 that
, 
, and 
are algebraically independent.
The number
is related to the lemniscate constant S by
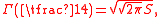
and it has been conjectured that
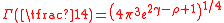
where ρ is the Masser-Gramain constant .
Borwein and Zucker have found that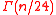
can be expressed algebraically in terms of π, 
, 
, 
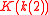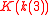, and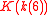 
where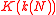 
is a complete elliptic integral of the first kind. This permits efficiently approximating the Gamma function of rational arguments to high precision using quadratically convergent arithmetic-geometric mean iterations. No similar relations are known for 
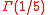or other denominators.
In particular,
is given by
Other formulas include the infinite products
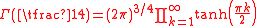
and
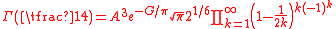
where A is the Glaisher-Kinkelin constant
and G is Catalan's constant.
C. H. Brown derived rapidly converging infinite series for particular values of the gamma function .:
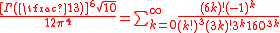
as well as,
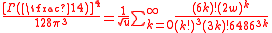
where,
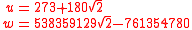
or, since 2w/6486^3 in fact is a cube involving u,
returns
It may also be given in terms of the Barnes G-function
:
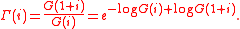
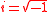returns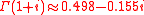
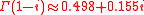
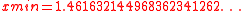
with the value
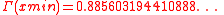
Integrating the reciprocal Gamma function along the positive real axis also gives the Fransén-Robinson constant.
On the negative real axis, the first local maxima and minima (zeros of the Digamma function)
are:
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
is an important special function in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. Its particular values can be expressed in closed form for integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
and half-integer
Half-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
arguments, but no simple expressions are known for the values at rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
points in general. Other fractional arguments can be approximated through efficient infinite products, infinite series, and recurrence relations.
Integers and half-integers
For positive integer arguments, the Gamma function coincides with the factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
, that is,
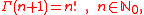
and hence
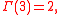
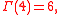
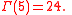
For non-positive integers, the Gamma function is not defined.
For positive half-integers, the function values are given exactly by
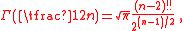
or equivalently, for non-negative integer values of n:
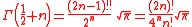
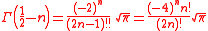
where n!! denotes the double factorial. In particular,
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
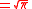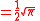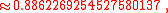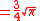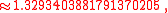and by means of the reflection formula
Reflection formula
In mathematics, a reflection formula or reflection relation for a function f is a relationship between f and f...
,
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
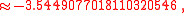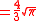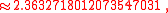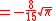General rational arguments
In analogy with the half-integer formula,where
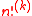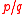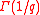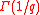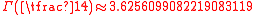
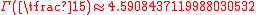
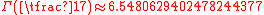
denotes the k:th multifactorial of n. By exploiting such functional relations, the Gamma function of any rational argument can be expressed in closed algebraic form in terms of . However, no closed expressions are known for the numbers where q > 2. Numerically, It is unknown whether these constants are transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
in general, but
and were shown to be transcendental by ChudnovskyChudnovsky
Chudnovsky may refer to*Chudnovsky brothers, David and Gregory, mathematicians*David Chudnovsky in Canada*Maria Chudnovsky, mathematics professor*Chudnofsky, the main villain of The Green Hornet...
.
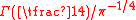has also long been known to be transcendental, and Yuri NesterenkoYuri Valentinovich Nesterenko
Yuri Valentinovich Nesterenko is a mathematician who has written papers in algebraic independence theory and transcendental number theory.In 1997 he was awarded the Ostrowski Prize for his proof that the numbers π and eπ are algebraically independent...
proved in 1996 that
, , and are algebraically independent.The number
is related to the lemniscate constant S by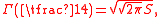and it has been conjectured that
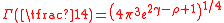
where ρ is the Masser-Gramain constant .
Borwein and Zucker have found that
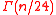can be expressed algebraically in terms of π, , , 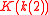, 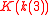and 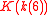where 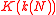is a complete elliptic integral of the first kind. This permits efficiently approximating the Gamma function of rational arguments to high precision using quadratically convergent arithmetic-geometric mean iterations. No similar relations are known for 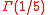or other denominators.In particular,
is given byOther formulas include the infinite products
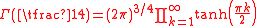
and
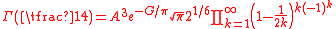
where A is the Glaisher-Kinkelin constant
Glaisher-Kinkelin constant
In mathematics, the Glaisher–Kinkelin constant or Glaisher's constant, typically denoted A, is a mathematical constant, related to the K-function and the Barnes G-function. The constant appears in a number of sums and integrals, especially those involving Gamma functions and zeta functions...
and G is Catalan's constant.
C. H. Brown derived rapidly converging infinite series for particular values of the gamma function .:
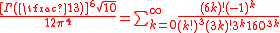
as well as,
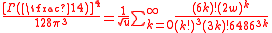
where,
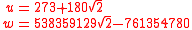
or, since 2w/6486^3 in fact is a cube involving u,
Imaginary unit
The gamma function on the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
returnsIt may also be given in terms of the Barnes G-function
Barnes G-function
In mathematics, the Barnes G-function G is a function that is an extension of superfactorials to the complex numbers. It is related to the Gamma function, the K-function and the Glaisher-Kinkelin constant, and was named after mathematician Ernest William Barnes...
:
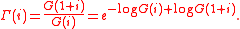
Complex Arguments
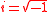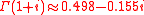
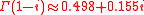
The gamma function with the complex Arguments returnsOther constants
The Gamma function has a local minimum on the positive real axis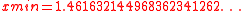 with the value
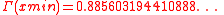
Integrating the reciprocal Gamma function along the positive real axis also gives the Fransén-Robinson constant.
On the negative real axis, the first local maxima and minima (zeros of the Digamma function)
are: