
Parametrix
Encyclopedia
In mathematics
, and specifically the field of partial differential equations (PDEs), a parametrix is an approximation to a fundamental solution
of a PDE, and is essentially an approximate inverse to a differential operator.
A parametrix for a differential operator is often easier to construct than a fundamental solution, and for many purposes is almost as good. It is sometimes possible to construct a fundamental solution from a parametrix by iteratively improving it.
P(D) with constant coefficients is: it is a distribution
u on ℝn such that

in the weak sense
, where δ is the Dirac delta distribution. In a similar way, a parametrix for a variable coefficient differential operator P(x,D) is a distribution u such that
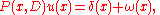
where ω is some C∞ function with compact support. The parametrix is a useful concept in the study of elliptic differential operators and, more generally, of hypoelliptic pseudodifferential operators with variable coefficient, since for such operators over appropriate domains a parametrix can be shown to exist, can be somewhat easily constructed and be a smooth function
away from the origin. Having found the analytic expression of the parametrix, it is possible to compute the solution of the associated fairly general elliptic partial differential equation by solving an associated Fredholm integral equation
: also, the structure itself of the parametrix reveals properties of the solution of the problem without even calculating it, like its smoothness and other qualitative properties
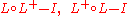
are both pseudodifferential operators of negative order. The operators L and L+ will admit continuous extensions to maps between the Sobolev spaces Hs and Hs+k. On a compact manifold, the differences above are compact operator
s. In this case the original operator L defines a Fredholm operator
between the Sobolev spaces.
. It can be applied to the Laplace operator
, the wave equation
and the heat equation
.
In the case of the heat equation or the wave equation, where there is a distinguished time parameter t,
Hadamard's method consists in taking the fundamental solution
of the constant coefficient differential operator obtained freezing the coefficients at a fixed point and seeking a general solution as a product of this solution, as the point varies, by a formal power series in t. The constant term is 1 and the higher coefficients are functions determined recursively as integrals in a single variable. In general the power series will not converge but will provide only an asymptotic expansion
of the exact solution. A suitable truncation of the power series then yields a parametrix.
If L is an element of a ring with multiplication * such that
for some approximate right inverse P and "sufficiently small" remainder term R then, at least formally,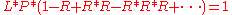
so if the infinite series makes sense then L has a right inverse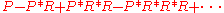 .
.
If L is a pseudo-differential operator and P is a parametrix, this gives a right inverse to L, in other words a fundamental solution, provided that R is "small enough" which in practice means that it should be a sufficiently good smoothing operator. If P and R are represented by functions, then the multiplication * of pseudo-differential operators corresponds to convolution of functions, so the terms of the infinite sum giving the fundamental solution of L involve convolution of P with copies of R.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and specifically the field of partial differential equations (PDEs), a parametrix is an approximation to a fundamental solution
Fundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
of a PDE, and is essentially an approximate inverse to a differential operator.
A parametrix for a differential operator is often easier to construct than a fundamental solution, and for many purposes is almost as good. It is sometimes possible to construct a fundamental solution from a parametrix by iteratively improving it.
Overview and informal definition
It is useful to start reviewing what a fundamental solution for a differential operatorDifferential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
P(D) with constant coefficients is: it is a distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
u on ℝn such that

in the weak sense
Weak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
, where δ is the Dirac delta distribution. In a similar way, a parametrix for a variable coefficient differential operator P(x,D) is a distribution u such that
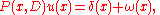
where ω is some C∞ function with compact support. The parametrix is a useful concept in the study of elliptic differential operators and, more generally, of hypoelliptic pseudodifferential operators with variable coefficient, since for such operators over appropriate domains a parametrix can be shown to exist, can be somewhat easily constructed and be a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
away from the origin. Having found the analytic expression of the parametrix, it is possible to compute the solution of the associated fairly general elliptic partial differential equation by solving an associated Fredholm integral equation
Fredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm.-Equation of the first kind :...
: also, the structure itself of the parametrix reveals properties of the solution of the problem without even calculating it, like its smoothness and other qualitative properties
Parametrices for pseudodifferential operators
More generally, if L is any pseudodifferential operator of order p, then another pseudodifferential operator L+ of order –p is called a parametrix for L if the operators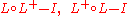
are both pseudodifferential operators of negative order. The operators L and L+ will admit continuous extensions to maps between the Sobolev spaces Hs and Hs+k. On a compact manifold, the differences above are compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
s. In this case the original operator L defines a Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
between the Sobolev spaces.
Hadamard parametrix construction
An explicit construction of a parametrix for second order partial differential operators based on power series developments was discovered by Jacques HadamardJacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
. It can be applied to the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
and the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
.
In the case of the heat equation or the wave equation, where there is a distinguished time parameter t,
Hadamard's method consists in taking the fundamental solution
of the constant coefficient differential operator obtained freezing the coefficients at a fixed point and seeking a general solution as a product of this solution, as the point varies, by a formal power series in t. The constant term is 1 and the higher coefficients are functions determined recursively as integrals in a single variable. In general the power series will not converge but will provide only an asymptotic expansion
Asymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
of the exact solution. A suitable truncation of the power series then yields a parametrix.
Construction of a fundamental solution from a parametrix
A sufficiently good parametrix can often be used to construct an exact fundamental solution by a convergent iterative procedure as follows .If L is an element of a ring with multiplication * such that

for some approximate right inverse P and "sufficiently small" remainder term R then, at least formally,
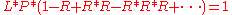
so if the infinite series makes sense then L has a right inverse
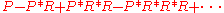 .
.If L is a pseudo-differential operator and P is a parametrix, this gives a right inverse to L, in other words a fundamental solution, provided that R is "small enough" which in practice means that it should be a sufficiently good smoothing operator. If P and R are represented by functions, then the multiplication * of pseudo-differential operators corresponds to convolution of functions, so the terms of the infinite sum giving the fundamental solution of L involve convolution of P with copies of R.

