
Parametric oscillator
Encyclopedia
A parametric oscillator is a harmonic oscillator
whose parameters oscillate in time. For example, a well known parametric oscillator is a child pumping a swing by periodically standing and squatting to increase the size of the swing's oscillations. The varying of the parameters drives the system. Examples of parameters that may be varied are its resonance frequency and damping
and damping 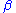 .
.
Parametric oscillators are used in many applications. The classical varactor parametric oscillator will oscillate when the diode's capacitance is varied periodically. The circuit that varies the diode's capacitance is called the "pump" or "driver". In microwave electronics, waveguide
/YAG based parametric oscillators operate in the same fashion. The designer varies a parameter periodically in order to induce oscillations.
Parametric oscillators have been developed as low-noise amplifiers, especially in the radio and microwave frequency range. Thermal noise is minimal, since a reactance (not a resistance) is varied. Another common use is frequency conversion, e.g., conversion from audio to radio frequencies. For example, the Optical parametric oscillator
converts an input laser
wave into two output waves of lower frequency (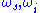 ).
).
Parametric resonance occurs in a mechanical system when a system is parametrically excited and oscillates at one of its resonant frequencies. Parametric excitation differs from forcing since the action appears as a time varying modification on a system parameter. This effect is different from regular resonance because it exhibits the instability
phenomenon.
(1831) was the first to notice oscillations of one frequency being excited by forces of double the frequency, in the crispations (ruffled surface waves) observed in a wine glass excited to "sing". Melde (1859) generated parametric oscillations in a string by employing a tuning fork to periodically vary the tension at twice the resonance frequency of the string. Parametric oscillation was first treated as a general phenomenon by Rayleigh
(1883,1887), whose papers are still worth reading today.
Parametric amplifiers (paramps) were first used in 1913-1915 for radio telephony from Berlin to Vienna and Moscow, and were predicted to have a useful future (Ernst Alexanderson
, 1916). The early paramps varied inductances, but other methods have been developed since, e.g., the varactor diodes, klystron tubes, Josephson junctions and optical methods
.
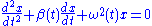
This equation is linear in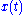 . By assumption, the parameters
. By assumption, the parameters
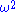 and
and 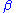 depend only on time and do not depend on the state of the oscillator. In general,
depend only on time and do not depend on the state of the oscillator. In general, 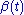 and/or
and/or 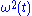 are assumed to vary periodically, with the same period
are assumed to vary periodically, with the same period 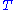 .
.
Remarkably, if the parameters vary at roughly twice the natural frequency of the oscillator (defined below), the oscillator phase-locks to the parametric variation and absorbs energy at a rate proportional to the energy it already has. Without a compensating energy-loss mechanism provided by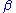 , the oscillation amplitude grows exponentially. (This phenomenon is called parametric excitation, parametric resonance or parametric pumping.) However, if the initial amplitude is zero, it will remain so; this distinguishes it from the non-parametric resonance of driven simple harmonic oscillator
, the oscillation amplitude grows exponentially. (This phenomenon is called parametric excitation, parametric resonance or parametric pumping.) However, if the initial amplitude is zero, it will remain so; this distinguishes it from the non-parametric resonance of driven simple harmonic oscillator
s, in which the amplitude grows linearly in time regardless of the initial state.
A familiar experience of both parametric and driven oscillation is playing on a swing. Rocking back and forth pumps the swing as a driven harmonic oscillator, but once moving, the swing can also be parametrically driven by alternately standing and squatting at key points in the swing. This changes moment of inertia of the swing and hence the resonance frequency, and children can quickly reach large amplitudes provided that they have some amplitude to start with (e.g., get a push). Standing and squatting at rest, however, goes nowhere.
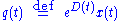
where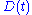 is a time integral of the damping
is a time integral of the damping
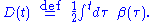
This change of variables eliminates the damping term

where the transformed frequency is defined

In general, the variations in damping and frequency are relatively small perturbations

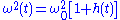
where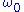 and
and 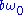 are constants, namely, the time-averaged oscillator frequency and damping, respectively. The transformed frequency can be written in a similar way:
are constants, namely, the time-averaged oscillator frequency and damping, respectively. The transformed frequency can be written in a similar way:
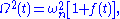
where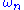 is the natural frequency of the damped harmonic oscillator
is the natural frequency of the damped harmonic oscillator
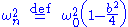
and
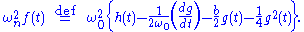
Thus, our transformed equation can be written
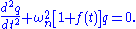
Remarkably, the independent variations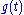 and
and  in the oscillator damping and resonance frequency, respectively, can be combined into a single pumping function
in the oscillator damping and resonance frequency, respectively, can be combined into a single pumping function 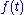 . The converse conclusion is that any form of parametric excitation can be accomplished by varying either the resonance frequency or the damping, or both.
. The converse conclusion is that any form of parametric excitation can be accomplished by varying either the resonance frequency or the damping, or both.
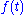 is sinusoidal, specifically
is sinusoidal, specifically
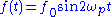
where the pumping frequency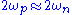 but need not equal
but need not equal  exactly. The solution
exactly. The solution 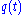 of our transformed equation may be written
of our transformed equation may be written
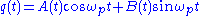
where we have factored out the rapidly varying components ( and
and  ) to isolate the slowly varying amplitudes
) to isolate the slowly varying amplitudes 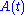 and
and 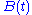 . This corresponds to Laplace's variation of parameters method.
. This corresponds to Laplace's variation of parameters method.
Substituting this solution into the transformed equation and retaining only the terms first-order in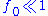 yields two coupled equations
yields two coupled equations
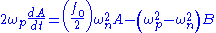
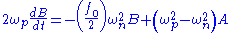
We may decouple and solve these equations by making another change of variables
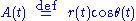

which yields the equations


where we have defined for brevity


and the detuning
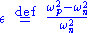
The equation does not depend on
equation does not depend on  , and linearization near its equilibrium position
, and linearization near its equilibrium position  shows that
shows that 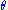 decays exponentially to its equilibrium
decays exponentially to its equilibrium
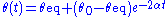
where the decay constant
 .
.
In other words, the parametric oscillator phase-locks to the pumping signal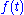 .
.
Taking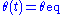 (i.e., assuming that the phase has locked), the
(i.e., assuming that the phase has locked), the  equation becomes
equation becomes
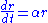
whose solution is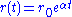 ; the amplitude of the
; the amplitude of the 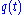 oscillation diverges exponentially. However, the corresponding amplitude
oscillation diverges exponentially. However, the corresponding amplitude 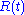 of the untransformed variable
of the untransformed variable 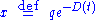 need not diverge
need not diverge
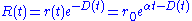
The amplitude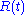 diverges, decays or stays constant, depending on whether
diverges, decays or stays constant, depending on whether 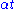 is greater than, less than, or equal to
is greater than, less than, or equal to 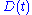 , respectively.
, respectively.
The maximum growth rate of the amplitude occurs when . At that frequency, the equilibrium phase
. At that frequency, the equilibrium phase  is zero, implying that
is zero, implying that 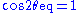 and
and 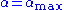 . As
. As  is varied from
is varied from  ,
,  moves away from zero and
moves away from zero and 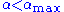 , i.e., the amplitude grows more slowly. For sufficiently large deviations of
, i.e., the amplitude grows more slowly. For sufficiently large deviations of 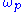 , the decay constant
, the decay constant  can become purely imaginary since
can become purely imaginary since

If the detuning exceeds
exceeds  ,
,  becomes purely imaginary and
becomes purely imaginary and 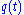 varies sinusoidally. Using the definition of the detuning
varies sinusoidally. Using the definition of the detuning  , the pumping frequency
, the pumping frequency 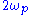 must lie between
must lie between 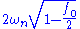 and
and  in order to achieve exponetial growth in
in order to achieve exponetial growth in 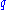 . Expanding the square roots in a binomial series shows that the spread in pumping frequencies that result in exponentially growing
. Expanding the square roots in a binomial series shows that the spread in pumping frequencies that result in exponentially growing 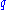 is approximately
is approximately  .
.
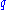 equation may be written in the form
equation may be written in the form
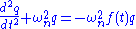
which represents a simple harmonic oscillator (or, alternatively, a bandpass filter) being driven by a signal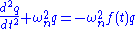 that is proportional to its response
that is proportional to its response 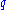 .
.
Assume that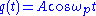 already has an oscillation at frequency
already has an oscillation at frequency 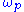 and that the pumping
and that the pumping 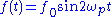 has double the frequency and a small amplitude
has double the frequency and a small amplitude 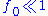 . Applying a trigonometric identity
. Applying a trigonometric identity
for products of sinusoids, their product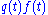 produces two driving signals,
produces two driving signals,
one at frequency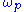 and the other at frequency
and the other at frequency 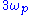
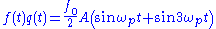
Being off-resonance, the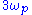 signal is attentuated and can be neglected initially. By contrast, the
signal is attentuated and can be neglected initially. By contrast, the 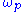 signal is on resonance, serves to amplify
signal is on resonance, serves to amplify 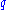 and is proportional to the amplitude
and is proportional to the amplitude
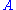 . Hence, the amplitude of
. Hence, the amplitude of 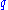 grows exponentially unless it is initially zero.
grows exponentially unless it is initially zero.
Expressed in Fourier space, the multiplication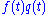 is a convolution of their Fourier transforms
is a convolution of their Fourier transforms 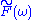 and
and 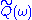 . The positive feedback arises because the
. The positive feedback arises because the 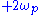 component of
component of 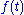 converts the
converts the 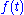 component of
component of 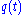 into a driving signal at
into a driving signal at
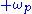 , and vice versa (reverse the signs). This explains why the pumping frequency must be near
, and vice versa (reverse the signs). This explains why the pumping frequency must be near 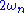 , twice the natural frequency of the oscillator. Pumping at a grossly different frequency would not couple (i.e., provide mutual positive feedback) between the
, twice the natural frequency of the oscillator. Pumping at a grossly different frequency would not couple (i.e., provide mutual positive feedback) between the 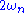 and
and 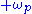 components of
components of 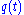 .
.
al resonance
phenomenon
of mechanical excitation
and oscillation
at certain frequenc
ies (and the associated harmonic
s). This effect is different from regular resonance because it exhibits the instability
phenomenon.
Parametric resonance occurs in a mechanical system when a system is parametrically excited and oscillates at one of its resonant frequencies.Parametric resonance takes place when the external excitation frequency equals to twice the natural frequency of the system. Parametric excitation differs from forcing since the action appears as a time varying modification on a system parameter. The classical example of parametric resonance is that of the vertically forced pendulum.
For small amplitudes and by linearising, the stability of the periodic solution is given by :
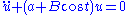
where is some perturbation from the periodic solution. Here the
is some perturbation from the periodic solution. Here the 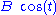 term acts as an ‘energy’ source and is said to parametrically excite the system. The Mathieu equation describes many other physical systems to a sinusoidal parametric excitation such as an LC Circuit where the capacitor plates move sinusoidally.
term acts as an ‘energy’ source and is said to parametrically excite the system. The Mathieu equation describes many other physical systems to a sinusoidal parametric excitation such as an LC Circuit where the capacitor plates move sinusoidally.
. The mixer's gain shows up in the output as amplifier gain. The input weak signal is mixed with a strong local oscillator signal, and the resultant strong output is used in the ensuing receiver stages.
Parametric amplifiers also operate by changing a parameter of the amplifier.
Intuitively, this can be understood as follows, for a variable capacitor based amplifier.
Q [charge in a capacitor] = C x V
therefore
V [voltage across a capacitor] = Q/C
Knowing the above, if a capacitor is charged until its voltage equals the sampled voltage of an incoming weak signal, and if the capacitor's capacitance is then reduced (say, by manually moving the plates further apart), then the voltage across the capacitor will increase. In this way, the voltage of the weak signal is amplified.
If the capacitor is a varicap diode, then the 'moving the plates' can be done simply by applying time-varying DC voltage to the varicap diode. This driving voltage usually comes from another oscillator — sometimes called a "pump".
The resulting output signal contains frequencies that are the sum and difference of the input signal (f1) and the pump signal (f2): (f1 + f2) and (f1 - f2).
A practical parametric oscillator needs the following connections: one for the "common" or "ground", one to feed the pump, one to retrieve the output, and maybe a fourth one for biasing. A parametric amplifier needs a fifth port to input the signal being amplified. Since a varactor diode has only two connections, it can only be a part of an LC network with four eigenvectors with nodes at the connections. This can be implemented as a transimpedance amplifier, a traveling wave amplifier or by means of a circulator
.
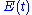 :
:

We assume that the damping is sufficiently strong that, in the absence of the driving force
is sufficiently strong that, in the absence of the driving force  , the amplitude of the parametric oscillations does not diverge, i.e., that
, the amplitude of the parametric oscillations does not diverge, i.e., that  . In this situation, the parametric pumping acts to lower the effective damping in the system. For illustration, let the damping be constant
. In this situation, the parametric pumping acts to lower the effective damping in the system. For illustration, let the damping be constant 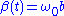 and assume that the external driving force is at the mean resonance frequency
and assume that the external driving force is at the mean resonance frequency 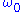 , i.e.,
, i.e., 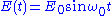 . The equation becomes
. The equation becomes

whose solution is roughly

As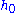 approaches the threshold
approaches the threshold 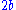 , the amplitude diverges. When
, the amplitude diverges. When 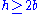 , the system enters parametric resonance and the amplitude begins to grow exponentially, even in the absence of a driving force
, the system enters parametric resonance and the amplitude begins to grow exponentially, even in the absence of a driving force 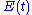 .
.
2:low noise level amplifier for ultra high frequency and microwave radio signal.
The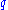 equation above with periodically varying
equation above with periodically varying  is an example of a Hill equation. If
is an example of a Hill equation. If 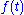 is a simple sinusoid, the equation is called a Mathieu equation.
is a simple sinusoid, the equation is called a Mathieu equation.
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
whose parameters oscillate in time. For example, a well known parametric oscillator is a child pumping a swing by periodically standing and squatting to increase the size of the swing's oscillations. The varying of the parameters drives the system. Examples of parameters that may be varied are its resonance frequency
 and damping
and damping 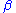 .
.Parametric oscillators are used in many applications. The classical varactor parametric oscillator will oscillate when the diode's capacitance is varied periodically. The circuit that varies the diode's capacitance is called the "pump" or "driver". In microwave electronics, waveguide
Waveguide (electromagnetism)
In electromagnetics and communications engineering, the term waveguide may refer to any linear structure that conveys electromagnetic waves between its endpoints. However, the original and most common meaning is a hollow metal pipe used to carry radio waves...
/YAG based parametric oscillators operate in the same fashion. The designer varies a parameter periodically in order to induce oscillations.
Parametric oscillators have been developed as low-noise amplifiers, especially in the radio and microwave frequency range. Thermal noise is minimal, since a reactance (not a resistance) is varied. Another common use is frequency conversion, e.g., conversion from audio to radio frequencies. For example, the Optical parametric oscillator
Optical parametric oscillator
An optical parametric oscillator is a parametric oscillator which oscillates at optical frequencies. It converts an input laser wave into two output waves of lower frequency by means of second order nonlinear optical interaction. The sum of the output waves frequencies is equal to the input wave...
converts an input laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
wave into two output waves of lower frequency (
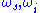 ).
).Parametric resonance occurs in a mechanical system when a system is parametrically excited and oscillates at one of its resonant frequencies. Parametric excitation differs from forcing since the action appears as a time varying modification on a system parameter. This effect is different from regular resonance because it exhibits the instability
Instability
In numerous fields of study, the component of instability within a system is generally characterized by some of the outputs or internal states growing without bounds...
phenomenon.
History
Michael FaradayMichael Faraday
Michael Faraday, FRS was an English chemist and physicist who contributed to the fields of electromagnetism and electrochemistry....
(1831) was the first to notice oscillations of one frequency being excited by forces of double the frequency, in the crispations (ruffled surface waves) observed in a wine glass excited to "sing". Melde (1859) generated parametric oscillations in a string by employing a tuning fork to periodically vary the tension at twice the resonance frequency of the string. Parametric oscillation was first treated as a general phenomenon by Rayleigh
John Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
(1883,1887), whose papers are still worth reading today.
Parametric amplifiers (paramps) were first used in 1913-1915 for radio telephony from Berlin to Vienna and Moscow, and were predicted to have a useful future (Ernst Alexanderson
Ernst Alexanderson
Ernst Frederick Werner Alexanderson was a Swedish-American electrical engineer, who was a pioneer in radio and television development.-Background:...
, 1916). The early paramps varied inductances, but other methods have been developed since, e.g., the varactor diodes, klystron tubes, Josephson junctions and optical methods
Optical parametric oscillator
An optical parametric oscillator is a parametric oscillator which oscillates at optical frequencies. It converts an input laser wave into two output waves of lower frequency by means of second order nonlinear optical interaction. The sum of the output waves frequencies is equal to the input wave...
.
The mathematics
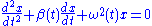
This equation is linear in
 . By assumption, the parameters
. By assumption, the parameters and
and  depend only on time and do not depend on the state of the oscillator. In general,
depend only on time and do not depend on the state of the oscillator. In general, 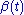 and/or
and/or 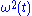 are assumed to vary periodically, with the same period
are assumed to vary periodically, with the same period 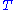 .
.Remarkably, if the parameters vary at roughly twice the natural frequency of the oscillator (defined below), the oscillator phase-locks to the parametric variation and absorbs energy at a rate proportional to the energy it already has. Without a compensating energy-loss mechanism provided by
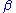 , the oscillation amplitude grows exponentially. (This phenomenon is called parametric excitation, parametric resonance or parametric pumping.) However, if the initial amplitude is zero, it will remain so; this distinguishes it from the non-parametric resonance of driven simple harmonic oscillator
, the oscillation amplitude grows exponentially. (This phenomenon is called parametric excitation, parametric resonance or parametric pumping.) However, if the initial amplitude is zero, it will remain so; this distinguishes it from the non-parametric resonance of driven simple harmonic oscillatorHarmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
s, in which the amplitude grows linearly in time regardless of the initial state.
A familiar experience of both parametric and driven oscillation is playing on a swing. Rocking back and forth pumps the swing as a driven harmonic oscillator, but once moving, the swing can also be parametrically driven by alternately standing and squatting at key points in the swing. This changes moment of inertia of the swing and hence the resonance frequency, and children can quickly reach large amplitudes provided that they have some amplitude to start with (e.g., get a push). Standing and squatting at rest, however, goes nowhere.
Transformation of the equation
We begin by making a change of variables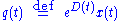
where
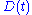 is a time integral of the damping
is a time integral of the damping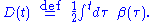
This change of variables eliminates the damping term

where the transformed frequency is defined

In general, the variations in damping and frequency are relatively small perturbations

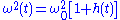
where
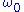 and
and 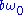 are constants, namely, the time-averaged oscillator frequency and damping, respectively. The transformed frequency can be written in a similar way:
are constants, namely, the time-averaged oscillator frequency and damping, respectively. The transformed frequency can be written in a similar way: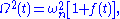
where
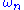 is the natural frequency of the damped harmonic oscillator
is the natural frequency of the damped harmonic oscillator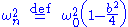
and
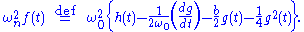
Thus, our transformed equation can be written
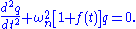
Remarkably, the independent variations
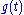 and
and  in the oscillator damping and resonance frequency, respectively, can be combined into a single pumping function
in the oscillator damping and resonance frequency, respectively, can be combined into a single pumping function 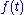 . The converse conclusion is that any form of parametric excitation can be accomplished by varying either the resonance frequency or the damping, or both.
. The converse conclusion is that any form of parametric excitation can be accomplished by varying either the resonance frequency or the damping, or both.Solution of the transformed equation
Let us assume that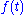 is sinusoidal, specifically
is sinusoidal, specifically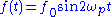
where the pumping frequency
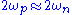 but need not equal
but need not equal  exactly. The solution
exactly. The solution 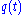 of our transformed equation may be written
of our transformed equation may be written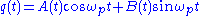
where we have factored out the rapidly varying components (
 and
and  ) to isolate the slowly varying amplitudes
) to isolate the slowly varying amplitudes 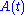 and
and 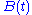 . This corresponds to Laplace's variation of parameters method.
. This corresponds to Laplace's variation of parameters method.Substituting this solution into the transformed equation and retaining only the terms first-order in
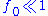 yields two coupled equations
yields two coupled equations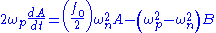
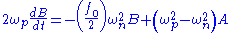
We may decouple and solve these equations by making another change of variables
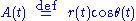

which yields the equations


where we have defined for brevity


and the detuning
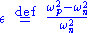
The
 equation does not depend on
equation does not depend on  , and linearization near its equilibrium position
, and linearization near its equilibrium position  shows that
shows that 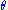 decays exponentially to its equilibrium
decays exponentially to its equilibrium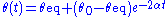
where the decay constant
 .
.In other words, the parametric oscillator phase-locks to the pumping signal
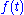 .
.Taking
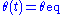 (i.e., assuming that the phase has locked), the
(i.e., assuming that the phase has locked), the  equation becomes
equation becomes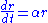
whose solution is
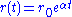 ; the amplitude of the
; the amplitude of the 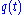 oscillation diverges exponentially. However, the corresponding amplitude
oscillation diverges exponentially. However, the corresponding amplitude 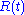 of the untransformed variable
of the untransformed variable 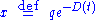 need not diverge
need not diverge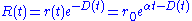
The amplitude
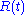 diverges, decays or stays constant, depending on whether
diverges, decays or stays constant, depending on whether 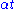 is greater than, less than, or equal to
is greater than, less than, or equal to 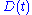 , respectively.
, respectively.The maximum growth rate of the amplitude occurs when
 . At that frequency, the equilibrium phase
. At that frequency, the equilibrium phase  is zero, implying that
is zero, implying that 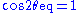 and
and 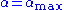 . As
. As  is varied from
is varied from  ,
,  moves away from zero and
moves away from zero and 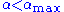 , i.e., the amplitude grows more slowly. For sufficiently large deviations of
, i.e., the amplitude grows more slowly. For sufficiently large deviations of 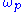 , the decay constant
, the decay constant  can become purely imaginary since
can become purely imaginary since
If the detuning
 exceeds
exceeds  ,
,  becomes purely imaginary and
becomes purely imaginary and 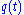 varies sinusoidally. Using the definition of the detuning
varies sinusoidally. Using the definition of the detuning  , the pumping frequency
, the pumping frequency 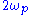 must lie between
must lie between 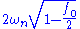 and
and  in order to achieve exponetial growth in
in order to achieve exponetial growth in 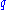 . Expanding the square roots in a binomial series shows that the spread in pumping frequencies that result in exponentially growing
. Expanding the square roots in a binomial series shows that the spread in pumping frequencies that result in exponentially growing 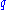 is approximately
is approximately  .
.Intuitive derivation of parametric excitation
The above derivation may seem like a mathematical sleight-of-hand, so it may be helpful to give an intuitive derivation. The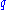 equation may be written in the form
equation may be written in the form
which represents a simple harmonic oscillator (or, alternatively, a bandpass filter) being driven by a signal
 that is proportional to its response
that is proportional to its response  .
.Assume that
 already has an oscillation at frequency
already has an oscillation at frequency 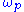 and that the pumping
and that the pumping 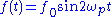 has double the frequency and a small amplitude
has double the frequency and a small amplitude 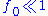 . Applying a trigonometric identity
. Applying a trigonometric identityTrigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
for products of sinusoids, their product
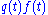 produces two driving signals,
produces two driving signals,one at frequency
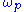 and the other at frequency
and the other at frequency 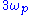
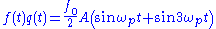
Being off-resonance, the
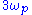 signal is attentuated and can be neglected initially. By contrast, the
signal is attentuated and can be neglected initially. By contrast, the 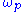 signal is on resonance, serves to amplify
signal is on resonance, serves to amplify 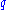 and is proportional to the amplitude
and is proportional to the amplitude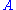 . Hence, the amplitude of
. Hence, the amplitude of 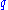 grows exponentially unless it is initially zero.
grows exponentially unless it is initially zero.Expressed in Fourier space, the multiplication
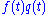 is a convolution of their Fourier transforms
is a convolution of their Fourier transforms 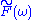 and
and 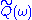 . The positive feedback arises because the
. The positive feedback arises because the 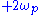 component of
component of 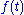 converts the
converts the 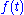 component of
component of 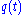 into a driving signal at
into a driving signal at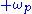 , and vice versa (reverse the signs). This explains why the pumping frequency must be near
, and vice versa (reverse the signs). This explains why the pumping frequency must be near 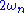 , twice the natural frequency of the oscillator. Pumping at a grossly different frequency would not couple (i.e., provide mutual positive feedback) between the
, twice the natural frequency of the oscillator. Pumping at a grossly different frequency would not couple (i.e., provide mutual positive feedback) between the 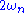 and
and 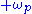 components of
components of 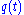 .
.Parametric resonance
Parametric resonance is the parametricParameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
al resonance
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
phenomenon
Phenomenon
A phenomenon , plural phenomena, is any observable occurrence. Phenomena are often, but not always, understood as 'appearances' or 'experiences'...
of mechanical excitation
Excitation
-Science:* The excited state of an atom* The excitatory postsynaptic potential* The excitation provided with an electrical generator or alternator-Agitation:*Excitement...
and oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
at certain frequenc
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
ies (and the associated harmonic
Harmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
s). This effect is different from regular resonance because it exhibits the instability
Instability
In numerous fields of study, the component of instability within a system is generally characterized by some of the outputs or internal states growing without bounds...
phenomenon.
Parametric resonance occurs in a mechanical system when a system is parametrically excited and oscillates at one of its resonant frequencies.Parametric resonance takes place when the external excitation frequency equals to twice the natural frequency of the system. Parametric excitation differs from forcing since the action appears as a time varying modification on a system parameter. The classical example of parametric resonance is that of the vertically forced pendulum.
For small amplitudes and by linearising, the stability of the periodic solution is given by :
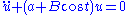
where
 is some perturbation from the periodic solution. Here the
is some perturbation from the periodic solution. Here the 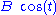 term acts as an ‘energy’ source and is said to parametrically excite the system. The Mathieu equation describes many other physical systems to a sinusoidal parametric excitation such as an LC Circuit where the capacitor plates move sinusoidally.
term acts as an ‘energy’ source and is said to parametrically excite the system. The Mathieu equation describes many other physical systems to a sinusoidal parametric excitation such as an LC Circuit where the capacitor plates move sinusoidally.Introduction
A parametric amplifier is implemented as a mixerFrequency mixer
In electronics a mixer or frequency mixer is a nonlinear electrical circuit that creates new frequencies from two signals applied to it. In its most common application, two signals at frequencies f1 and f2 are applied to a mixer, and it produces new signals at the sum f1 + f2 and difference f1 -...
. The mixer's gain shows up in the output as amplifier gain. The input weak signal is mixed with a strong local oscillator signal, and the resultant strong output is used in the ensuing receiver stages.
Parametric amplifiers also operate by changing a parameter of the amplifier.
Intuitively, this can be understood as follows, for a variable capacitor based amplifier.
Q [charge in a capacitor] = C x V
therefore
V [voltage across a capacitor] = Q/C
Knowing the above, if a capacitor is charged until its voltage equals the sampled voltage of an incoming weak signal, and if the capacitor's capacitance is then reduced (say, by manually moving the plates further apart), then the voltage across the capacitor will increase. In this way, the voltage of the weak signal is amplified.
If the capacitor is a varicap diode, then the 'moving the plates' can be done simply by applying time-varying DC voltage to the varicap diode. This driving voltage usually comes from another oscillator — sometimes called a "pump".
The resulting output signal contains frequencies that are the sum and difference of the input signal (f1) and the pump signal (f2): (f1 + f2) and (f1 - f2).
A practical parametric oscillator needs the following connections: one for the "common" or "ground", one to feed the pump, one to retrieve the output, and maybe a fourth one for biasing. A parametric amplifier needs a fifth port to input the signal being amplified. Since a varactor diode has only two connections, it can only be a part of an LC network with four eigenvectors with nodes at the connections. This can be implemented as a transimpedance amplifier, a traveling wave amplifier or by means of a circulator
Circulator
A circulator is a passive non-reciprocal three- or four-port device, in which microwave or radio frequency power entering any port is transmitted to the next port in rotation...
.
Mathematical equation
The parametric oscillator equation can be extended by adding an external driving force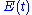 :
:
We assume that the damping
 is sufficiently strong that, in the absence of the driving force
is sufficiently strong that, in the absence of the driving force  , the amplitude of the parametric oscillations does not diverge, i.e., that
, the amplitude of the parametric oscillations does not diverge, i.e., that  . In this situation, the parametric pumping acts to lower the effective damping in the system. For illustration, let the damping be constant
. In this situation, the parametric pumping acts to lower the effective damping in the system. For illustration, let the damping be constant 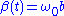 and assume that the external driving force is at the mean resonance frequency
and assume that the external driving force is at the mean resonance frequency 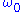 , i.e.,
, i.e., 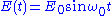 . The equation becomes
. The equation becomes
whose solution is roughly

As
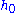 approaches the threshold
approaches the threshold 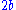 , the amplitude diverges. When
, the amplitude diverges. When 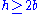 , the system enters parametric resonance and the amplitude begins to grow exponentially, even in the absence of a driving force
, the system enters parametric resonance and the amplitude begins to grow exponentially, even in the absence of a driving force 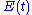 .
.Advantages
1:It is highly sensitive.2:low noise level amplifier for ultra high frequency and microwave radio signal.
Other relevant mathematical results
If the parameters of any second-order linear differential equation are varied periodically, Floquet analysis shows that the solutions must vary either sinusoidally or exponentially.The
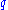 equation above with periodically varying
equation above with periodically varying  is an example of a Hill equation. If
is an example of a Hill equation. If 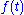 is a simple sinusoid, the equation is called a Mathieu equation.
is a simple sinusoid, the equation is called a Mathieu equation.See also
- Harmonic oscillatorHarmonic oscillatorIn classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
- Optical parametric oscillatorOptical parametric oscillatorAn optical parametric oscillator is a parametric oscillator which oscillates at optical frequencies. It converts an input laser wave into two output waves of lower frequency by means of second order nonlinear optical interaction. The sum of the output waves frequencies is equal to the input wave...
- Optical parametric amplifierOptical parametric amplifierAn optical parametric amplifier, abbreviated OPA, is a laser light source that emits light of variable wavelengths by an optical parametric amplification process.-Optical parametric generation :...
- Mathieu equation
Further reading
- Kühn L. (1914) Elektrotech. Z., 35, 816-819.
- Mumford WW. (1960) "Some Notes on the History of Parametric Transducers", Proceedings of the Institute of Radio Engineers, 48, 848-853.
- Pungs L. DRGM Nr. 588 822 (24 October 1913); DRP Nr. 281440 (1913); Elektrotech. Z., 44, 78-81 (1923?); Proc. IRE, 49, 378 (1961).
External articles
- Elmer, Franz-Josef, "Parametric Resonance". unibas.ch, July 20, 1998.
- Cooper, Jeffery, "Parametric Resonance in Wave Equations with a Time-Periodic Potential". SIAM Journal on Mathematical Analysis, Volume 31, Number 4, pp. 821–835. Society for Industrial and Applied Mathematics, 2000 .
- "Driven Pendulum: Parametric Resonance". phys.cmu.edu (Demonstration of physical mechanics or classical mechanics. Resonance oscillations set up in a simple pendulum via periodically varying pendulum length.)

