
Voigt notation
Encyclopedia
In mathematics
, Voigt notation or Voigt form in multilinear algebra
is a way to represent a symmetric tensor by reducing its order. There are a few variants and associated names for this idea: Mandel notation, Mandel–Voigt notation and Nye notation are others found. Kelvin notation is a revival by Helbig (1994) of old ideas of Lord Kelvin. The differences here lie in certain weights attached to the selected entries of the tensor. Nomenclature may vary according to what is traditional in the field of application.
For example, a 2×2 symmetric tensor X has only three distinct elements, the two on the diagonal and the other being off-diagonal. Thus it can be expressed as the vector
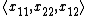 .
.
As another example:
The stress tensor (in matrix notation) is given as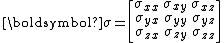
In Voigt notation it is simplified to a 6-dimensional vector: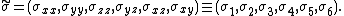
The strain tensor, similar in nature to the stress tensor -- both are symmetric second-order tensors --, is given in matrix form as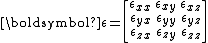
Its representation in Voigt notation is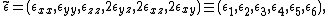
where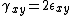 ,
, 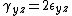 , and
, and  are engineering shear strains.
are engineering shear strains.
The benefit of using different representations for stress and strain is that the scalar invariance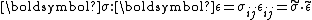
is preserved.
Likewise, a three-dimensional symmetric fourth-order tensor can be reduced to a 6×6 matrix.
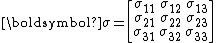
only six components are distinct, the three on the diagonal and the other being off-diagonal.
Thus it can be expressed, in Mandel notation, as the vector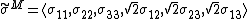
The main advantage of Mandel notation is to allow the use of the same conventional operations used with vectors,
for example: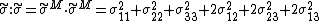
A symmetric tensor of rank four satisfying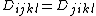 and
and  has 81 components in four-dimensional space, but only 36
has 81 components in four-dimensional space, but only 36
components are distinct. Thus, in Mandel notation, it can be expressed as
. It is useful, for example, in calculations involving constitutive models to simulate materials, such as the generalized Hooke's law
, as well as finite element analysis.
Hooke's law has a symmetric fourth-order stiffness tensor with 81 components (3×3×3×3). Voigt notation enables this to be simplified to a 6×6 matrix. However, Voigt's form does not preserve the sum of the squares, which in the case of Hooke's law has geometric significance. This explains why weights are introduced (to make the mapping an isometry
).
A discussion of invariance of Voigt's notation and Mandel's notation be found in Helnwein (2001).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Voigt notation or Voigt form in multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
is a way to represent a symmetric tensor by reducing its order. There are a few variants and associated names for this idea: Mandel notation, Mandel–Voigt notation and Nye notation are others found. Kelvin notation is a revival by Helbig (1994) of old ideas of Lord Kelvin. The differences here lie in certain weights attached to the selected entries of the tensor. Nomenclature may vary according to what is traditional in the field of application.
For example, a 2×2 symmetric tensor X has only three distinct elements, the two on the diagonal and the other being off-diagonal. Thus it can be expressed as the vector
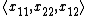 .
.As another example:
The stress tensor (in matrix notation) is given as
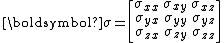
In Voigt notation it is simplified to a 6-dimensional vector:
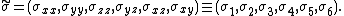
The strain tensor, similar in nature to the stress tensor -- both are symmetric second-order tensors --, is given in matrix form as
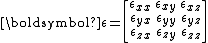
Its representation in Voigt notation is
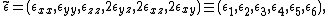
where
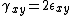 ,
, 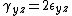 , and
, and  are engineering shear strains.
are engineering shear strains.The benefit of using different representations for stress and strain is that the scalar invariance
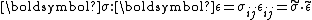
is preserved.
Likewise, a three-dimensional symmetric fourth-order tensor can be reduced to a 6×6 matrix.
Mandel notation
For a symmetric tensor of second rank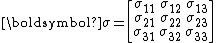
only six components are distinct, the three on the diagonal and the other being off-diagonal.
Thus it can be expressed, in Mandel notation, as the vector
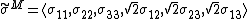
The main advantage of Mandel notation is to allow the use of the same conventional operations used with vectors,
for example:
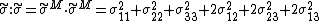
A symmetric tensor of rank four satisfying
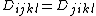 and
and  has 81 components in four-dimensional space, but only 36
has 81 components in four-dimensional space, but only 36components are distinct. Thus, in Mandel notation, it can be expressed as

Applications
The notation is named after physicist Woldemar VoigtWoldemar Voigt
Woldemar Voigt was a German physicist, who taught at the Georg August University of Göttingen. Voigt eventually went on to head the Mathematical Physics Department at Göttingen and was succeeded in 1914 by Peter Debye, who took charge of the theoretical department of the Physical Institute...
. It is useful, for example, in calculations involving constitutive models to simulate materials, such as the generalized Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
, as well as finite element analysis.
Hooke's law has a symmetric fourth-order stiffness tensor with 81 components (3×3×3×3). Voigt notation enables this to be simplified to a 6×6 matrix. However, Voigt's form does not preserve the sum of the squares, which in the case of Hooke's law has geometric significance. This explains why weights are introduced (to make the mapping an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
).
A discussion of invariance of Voigt's notation and Mandel's notation be found in Helnwein (2001).
See also
- Vectorization (mathematics)Vectorization (mathematics)In mathematics, especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a column vector...
- Hooke's lawHooke's lawIn mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
- P. Helnwein (2001). Some Remarks on the Compressed Matrix Representation of Symmetric Second-Order and Fourth-Order Tensors. Computer Methods in Applied Mechanics and Engineering, 190(22–23):2753–2770

