
Strain energy density function
Encyclopedia
A strain energy density function or stored energy density function is a scalar valued function
that relates the strain energy
density of a material to the deformation gradient.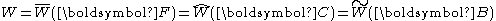
where is the (two-point) deformation gradient tensor
is the (two-point) deformation gradient tensor
, is the right Cauchy-Green deformation tensor, and
is the right Cauchy-Green deformation tensor, and 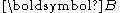 is the left Cauchy-Green deformation tensor .
is the left Cauchy-Green deformation tensor .
For an isotropic material, the deformation gradient can be expressed uniquely in terms of the principal stretches or in terms of the invariants
of the left Cauchy-Green deformation tensor or right Cauchy-Green deformation tensor and we have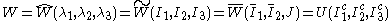
with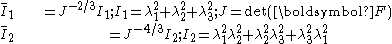
A strain energy density function is used to define a hyperelastic material
by postulating that the stress
in the material can be obtained by taking the derivative
of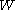 with respect to the strain. For an isotropic, hyperelastic material the function relates the energy
with respect to the strain. For an isotropic, hyperelastic material the function relates the energy
stored in an elastic material
, and thus the stress-strain relationship, only to the three strain
(elongation) components, thus disregarding the deformation history, heat dissipation, stress relaxation
etc.
The strain energy density function relates to the Helmholtz free energy
function ,
,
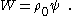
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that relates the strain energy
Strain energy
In a molecule, strain energy is released when the constituent atoms are allowed to rearrange themselves in a chemical reaction or a change of chemical conformation in a way that:* angle strain,* torsional strain,* ring strain and/or steric strain,...
density of a material to the deformation gradient.
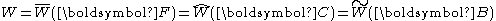
where
 is the (two-point) deformation gradient tensor
is the (two-point) deformation gradient tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
,
 is the right Cauchy-Green deformation tensor, and
is the right Cauchy-Green deformation tensor, and 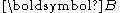 is the left Cauchy-Green deformation tensor .
is the left Cauchy-Green deformation tensor .For an isotropic material, the deformation gradient can be expressed uniquely in terms of the principal stretches or in terms of the invariants
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
of the left Cauchy-Green deformation tensor or right Cauchy-Green deformation tensor and we have
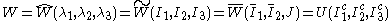
with
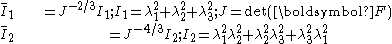
A strain energy density function is used to define a hyperelastic material
Hyperelastic material
A hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
by postulating that the stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
in the material can be obtained by taking the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of
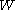 with respect to the strain. For an isotropic, hyperelastic material the function relates the energy
with respect to the strain. For an isotropic, hyperelastic material the function relates the energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
stored in an elastic material
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
, and thus the stress-strain relationship, only to the three strain
Strain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
(elongation) components, thus disregarding the deformation history, heat dissipation, stress relaxation
Stress relaxation
Stress relaxation describes how polymers relieve stress under constant strain. Because they are viscoelastic, polymers behave in a nonlinear, non-Hookean fashion...
etc.
The strain energy density function relates to the Helmholtz free energy
Helmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
function
 ,
,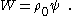
Examples of strain energy density functions
Some examples of hyperelastic constitutive equations are- Saint Venant–Kirchhoff
- Neo-HookeanNeo-Hookean solidA Neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948. In contrast to linear elastic materials, a the...
- Generalized RivlinPolynomial (hyperelastic model)The polynomial hyperelastic material model is a phenomenological model of rubber elasticity. In this model, the strain energy density function is of the form of a polynomial in the two invariants I_1,I_2 of the left Cauchy-Green deformation tensor....
- Mooney–Rivlin
- OgdenOgden (hyperelastic model)The Ogden material model is a hyperelastic material model used to describe the non-linear stress-strain behaviour of complex materials such as rubbers, polymers, and biological tissue. The model was developed by Ray W. Ogden in 1972...
- YeohYeoh (hyperelastic model)300px|right|thumb|Yeoh model prediction versus experimental data for natural rubber. Model parameters and experimental data from The Yeoh hyperelastic material model is a phenomenological model for the deformation of nearly incompressible, nonlinear elastic materials such as rubber...
- Arruda–Boyce model
- GentGent (hyperelastic model)The Gent hyperelastic material model is a phenomenological model of rubber elasticity that is based on the concept of limiting chain extensibility...
See also
- Helmholtz and Gibbs free energy in thermoelasticity
- Hyperelastic materialHyperelastic materialA hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
- Finite strain theory

