
Hermann-Mauguin notation
Encyclopedia
Hermann–Mauguin notation is used to represent the symmetry element
s in point group
s, plane groups and space group
s. It is named after the German crystallographer Carl Hermann
and the French mineralogist Charles-Victor Mauguin
. This notation is sometimes called international notation.
The Hermann–Mauguin notation, compared with the Schoenflies notation
, is preferred in crystallography
because it can easily be used to include translational symmetry elements, and it specifies the directions of the symmetry axes.
Thus, for example, a cube has three fourfold axes (through the centre of the faces), four threefold axes (through the long diagonals), and six twofold axes (through the centre of diagonally opposite edges). It also has nine mirror planes (three parallel to the faces, and six cutting the faces diagonally). Now note that one of the fourfold axes and one of the threefold axes will be sufficient to deduce the remaining three- and fourfold axes. Also note that given a mirror plane perpendicular to the fourfold axis allows us to deduce the other two mirror planes that are parallel to the faces. Finally, if we add one of the twofold axes and its perpendicular mirror plane then all the remaining mirror planes and twofold axes can be deduced. Hence we notate the symmetry of cube as "4/m2/m" or "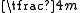
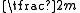 " (full symbol) or "mm" (short symbol).
" (full symbol) or "mm" (short symbol).
In three dimensions, there are 32 crystallographic point groups:
s are denoted g.
. Translations within the lattice in the form of screw axes and glide planes are also noted, giving a complete crystallographic space group. An example of a space group would be Garnet
 .
.
is noted by a number, n, where the angle of rotation is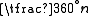 . The degree of translation is then added as a subscript showing how far along the axis the translation is, as a portion of the parallel lattice vector. For example, 21 is a 180° (twofold) rotation followed by a translation of ½ of the lattice vector. 31 is a 120° (threefold) rotation followed by a translation of ⅓ of the lattice vector.
. The degree of translation is then added as a subscript showing how far along the axis the translation is, as a portion of the parallel lattice vector. For example, 21 is a 180° (twofold) rotation followed by a translation of ½ of the lattice vector. 31 is a 120° (threefold) rotation followed by a translation of ⅓ of the lattice vector.
The possible screw axis are: 21, 31, 32, 41, 42, 43, 61, 62, 63, 64, and 65.
There are 4 enantiomorphic pairs
of axes: 31 and 32, 41 and 43, 61 and 65, and 62 and 64. This enantiomorphism results in 11 pairs of enantiomorphic space groups, namely
structure.
Symmetry element
A symmetry element is a point of reference about which symmetry operations can take place. In particular, symmetry elements can be centers of inversion, axes of rotation and mirror planes.-See also:* Symmetry* Group theory* Crystallography...
s in point group
Point group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
s, plane groups and space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s. It is named after the German crystallographer Carl Hermann
Carl Hermann
Carl Hermann was a German professor of crystallography. With Charles-Victor Mauguin, he invented an international standard notation for crystallographic groups known as the Hermann–Mauguin notation or International notation.Born in the north German port town of Wesermünde to parents both of...
and the French mineralogist Charles-Victor Mauguin
Charles-Victor Mauguin
French professor of mineralogy Charles-Victor Mauguin was inventor of an international standard notation for crystallographic groups known as the Hermann–Mauguin notation or International notation....
. This notation is sometimes called international notation.
The Hermann–Mauguin notation, compared with the Schoenflies notation
Schoenflies notation
The Schoenflies notation or Schönflies notation, named after the German mathematician Arthur Moritz Schoenflies, is one of two conventions commonly used to describe Point groups. This notation is used in spectroscopy. The other convention is the Hermann–Mauguin notation, also known as the...
, is preferred in crystallography
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
because it can easily be used to include translational symmetry elements, and it specifies the directions of the symmetry axes.
Nomenclature
Rotational symmetries are denoted by a number n, given by φ = 360° / n, where φ is the angle of rotation. A rotation of 180° would be denoted by n = 2, and is called a twofold rotation. By convention these are written down in decreasing order of n, with the largest called the principal axis. Next the additional symmetries of the axes are noted. Dihedral symmetry, where inversion through a point followed by rotation through an angle of φ = 360° / n recovers the original shape, is denoted by . For example, the space diagonal of a cube is . Each axis has zero or more mirror planes associated with it (meaning a mirror plane that is perpendicular to the axis or one that is parallel and intersects the axis). An "m" is written after each axis number for each (unique) mirror plane. If one of those mirrors is perpendicular to the axis then a slash "/" is placed between the axis number and the first "m" or Typically, if given a choice, one shows a mirror plane as a perpendicular.Thus, for example, a cube has three fourfold axes (through the centre of the faces), four threefold axes (through the long diagonals), and six twofold axes (through the centre of diagonally opposite edges). It also has nine mirror planes (three parallel to the faces, and six cutting the faces diagonally). Now note that one of the fourfold axes and one of the threefold axes will be sufficient to deduce the remaining three- and fourfold axes. Also note that given a mirror plane perpendicular to the fourfold axis allows us to deduce the other two mirror planes that are parallel to the faces. Finally, if we add one of the twofold axes and its perpendicular mirror plane then all the remaining mirror planes and twofold axes can be deduced. Hence we notate the symmetry of cube as "4/m2/m" or "
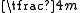
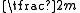 " (full symbol) or "mm" (short symbol).
" (full symbol) or "mm" (short symbol).Point groups
Point groups exist in both two and three dimensions. They are defined by their symmetry elements, such as the axes of proper and improper rotation and mirror planes. Translational symmetry elements which are present in plane groups and space groups are omitted. Where certain symmetry elements can be deduced, they may be omitted, allowing simplification.In three dimensions, there are 32 crystallographic point groups:
- 1,
- 2, m, 2⁄m
- 222, mm2, mmm
- 4, , 4⁄m, 422, 4mm, 2m, 4⁄mmm
- 3, , 32, 3m, m
- 6, , 6⁄m, 622, 6mm, 2m, 6⁄mmm
- 23, m, 432, 3m, mm
Plane groups
Plane groups can be depicted using the Hermann-Mauguin system. The first letter is either lowercase p or c to represent primitive or centered unit cells. The next number is the rotational symmetry, as given above. The presence of mirror planes are denoted m, while glide reflectionGlide reflection
In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...
s are denoted g.
Space groups
Space groups can be defined by combining the point group identifier with the uppercase letters describing the latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
. Translations within the lattice in the form of screw axes and glide planes are also noted, giving a complete crystallographic space group. An example of a space group would be Garnet
Garnet
The garnet group includes a group of minerals that have been used since the Bronze Age as gemstones and abrasives. The name "garnet" may come from either the Middle English word gernet meaning 'dark red', or the Latin granatus , possibly a reference to the Punica granatum , a plant with red seeds...
 .
.Lattice types
These are the Bravais lattices in three dimensions:- P primitive
- I body centered (from the German "Innenzentriert")
- F face centered (from the German "Flächenzentriert")
- A nodes on A faces only
- B nodes on B faces only
- C centered on the a,b or A,B face
- R rhombohedral
Screw axis
The screw axisScrew axis
The screw axis of an object is a line that is simultaneously the axis of rotation and the line along which a translation occurs...
is noted by a number, n, where the angle of rotation is
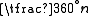 . The degree of translation is then added as a subscript showing how far along the axis the translation is, as a portion of the parallel lattice vector. For example, 21 is a 180° (twofold) rotation followed by a translation of ½ of the lattice vector. 31 is a 120° (threefold) rotation followed by a translation of ⅓ of the lattice vector.
. The degree of translation is then added as a subscript showing how far along the axis the translation is, as a portion of the parallel lattice vector. For example, 21 is a 180° (twofold) rotation followed by a translation of ½ of the lattice vector. 31 is a 120° (threefold) rotation followed by a translation of ⅓ of the lattice vector.The possible screw axis are: 21, 31, 32, 41, 42, 43, 61, 62, 63, 64, and 65.
There are 4 enantiomorphic pairs
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
of axes: 31 and 32, 41 and 43, 61 and 65, and 62 and 64. This enantiomorphism results in 11 pairs of enantiomorphic space groups, namely
| P41 | P4122 | P41212 | P31 | P3112 | P3121 | P61 | P62 | P6122 | P6222 | P4132 |
|---|---|---|---|---|---|---|---|---|---|---|
| P43 | P4322 | P43212 | P32 | P3212 | P3221 | P65 | P64 | P6522 | P6422 | P4332 |
Glide planes
Glide planes are noted by a, b, or c depending on which axis the glide is along. There is also the n glide, which is a glide along the half of a diagonal of a face, and the d glide, which is along a quarter of either a face or space diagonal of the unit cell. The d glide is often called the diamond glide plane as it features in the diamondDiamond
In mineralogy, diamond is an allotrope of carbon, where the carbon atoms are arranged in a variation of the face-centered cubic crystal structure called a diamond lattice. Diamond is less stable than graphite, but the conversion rate from diamond to graphite is negligible at ambient conditions...
structure.
 ,
, 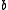 , or
, or  glide translation along half the lattice vector of this face
glide translation along half the lattice vector of this face glide translation along with half a face diagonal
glide translation along with half a face diagonal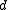 glide planes with translation along a quarter of a face diagonal.
glide planes with translation along a quarter of a face diagonal. two glides with the same glide plane and translation along two (different) half-lattice vectors.
two glides with the same glide plane and translation along two (different) half-lattice vectors.

