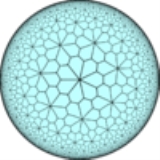
Order-3 snub heptagonal tiling
Encyclopedia
In geometry
, the order-3 snub heptagonal tiling is a semiregular tiling of the hyperbolic plane. There are four triangle
s, one heptagon on each vertex
. It has Schläfli symbol of s{7,3}.
polyhedra with vertex figure (3.3.3.3.p) and Coxeter-Dynkin diagram
. These face-transitive figures have (n32) rotational symmetry.
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the order-3 snub heptagonal tiling is a semiregular tiling of the hyperbolic plane. There are four triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s, one heptagon on each vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
. It has Schläfli symbol of s{7,3}.
Related polyhedra and tilings
This tiling is part of sequence of snubbedSnub (geometry)
In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided...
polyhedra with vertex figure (3.3.3.3.p) and Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
. These face-transitive figures have (n32) rotational symmetry.
 (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... (332) |
 (3.3.3.3.4) Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... (432) |
 (3.3.3.3.5) Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... (532) |
 3.3.3.3.6 Snub hexagonal tiling In geometry, the Snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex... (632) |
 3.3.3.3.7 (732) |
 3.3.3.3.8 (832) |
Dual tiling
The dual tiling is called an order-7-3 floret pentagonal tiling, and is related to the floret pentagonal tilingFloret pentagonal tiling
In geometry, the floret pentagonal tiling is a dual semiregular tiling of the Euclidean plane. It is one of 14 known isohedral pentagon tilings. It is given its name because its six pentagonal tiles radiate out from a central point, like petals on a flower...
.
See also
- Snub hexagonal tilingSnub hexagonal tilingIn geometry, the Snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex...
- Floret pentagonal tilingFloret pentagonal tilingIn geometry, the floret pentagonal tiling is a dual semiregular tiling of the Euclidean plane. It is one of 14 known isohedral pentagon tilings. It is given its name because its six pentagonal tiles radiate out from a central point, like petals on a flower...
- Floret pentagonal tiling
- Order-3 heptagonal tiling
- Tilings of regular polygons
- List of uniform planar tilings
- Kagome latticeKagome latticeA kagome lattice is an arrangement of laths composed of interlaced triangles such that each point where two laths cross has four neighboring points...


