
NL (complexity)
Encyclopedia
In computational complexity theory
, NL (Nondeterministic Logarithmic-space) is the complexity class
containing decision problem
s which can be solved by a nondeterministic Turing machine using a logarithm
ic amount of memory space.
NL is a generalization of L
, the class for logspace problems on a deterministic Turing machine. Since any deterministic Turing machine is also a nondeterministic Turing machine, we have that L is contained in NL.
NL can be formally defined in terms of the computational resource nondeterministic space (or NSPACE) as NL = NSPACE(log n).
Important results in complexity theory allow us to relate this complexity class with other classes, telling us about the relative power of the resources involved. Results in the field of algorithm
s, on the other hand, tell us which problems can be solved with this resource. Unfortunately, like much of complexity theory, many important questions about NL are still open
(see Unsolved problems in computer science).
Occasionally NL is referred to as RL due to its probabilistic definition below; however, this name is more frequently used to refer to randomized logarithmic space, which is not known to equal NL.
under log-space reduction
s, including ST-connectivity
and 2-satisfiability
. ST-connectivity
asks for nodes S and T in a directed graph
whether T is reachable
from S. 2-satisfiability
asks, given a formula of which each clause is the disjunction of two literals, if there is a variable assignment that makes the formula true. An example instance, where ~ indicates not, might be:
and (~x2 or x3) and (~x1 or ~x2)
, since there is a polynomial-time algorithm for 2-satisfiability
, but it is not known whether NL = P or whether L = NL. It is known that NL = co-NL, where co-NL is the complement
of NL. This result was independently discovered by Neil Immerman
and Róbert Szelepcsényi
in 1987 (Immerman-Szelepcsényi Theorem
), who received the 1995 Gödel Prize
for this work.
In circuit complexity
, NL can be placed within the NC
hierarchy. In Papadimitriou 1994, Theorem 16.1, we have:
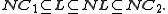
More precisely, NL is contained in AC1
. It is known that NL is equal to ZPL, the class of problems solvable by randomized algorithms in logarithmic space and unbounded time, with no error. It is not, however, known or believed to be equal to RLP or ZPLP, the polynomial-time restrictions of RL and ZPL which some authors refer to as RL and ZPL.
We can relate NL to deterministic space using Savitch's theorem
, which tells us that any nondeterministic algorithm can be simulated by a deterministic machine in at most quadratically more space. From Savitch's theorem, we have directly that:
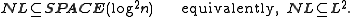
This was the strongest deterministic-space inclusion known (Papadimitriou 1994 Problem 16.4.10, "Symmetric space"). Since larger space classes are not affected by quadratic increases, the nondeterministic and deterministic classes are known to be equal, so that for example we have PSPACE
= NPSPACE.
of problems solvable in logarithmithic space with probabilistic Turing machine
s that never accept incorrectly but are allowed to reject incorrectly less than 1/3 of the time; this is called one-sided error. The constant 1/3 is arbitrary; any x with 0 ≤ x < 1/2 would suffice.
It turns out that C = NL. Notice that C, unlike its deterministic counterpart L
, is not limited to polynomial time, because although it has a polynomial number of configurations it can use randomness to escape an infinite loop. If we do limit it to polynomial time, we get the class RL, which is contained in but not known or believed to equal NL.
There is a simple algorithm which establishes that C = NL. Clearly C is contained in NL, since:
To show that NL is contained in C, we simply take an NL algorithm and choose a random computation path of length n, and do this 2n times. Because no computation path exceeds length n, and because there are 2n computation paths in all, we have a good chance of hitting the accepting one (bounded below by a constant).
The only problem is that we don't have room in log space for a binary counter that goes up to 2n. To get around this we replace it with a randomized counter, which simply flips n coins and stops and rejects if they all land on heads. Since this event has probability 2-n, we expect
to take 2n steps on average before stopping. It only needs to keep a running total of the number of heads in a row it sees, which it can count in log space.
Thus, when we only look at space alone, it seems that randomization and nondeterminism are equally powerful.
with an added transitive closure
operator.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, NL (Nondeterministic Logarithmic-space) is the complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
containing decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s which can be solved by a nondeterministic Turing machine using a logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic amount of memory space.
NL is a generalization of L
L (complexity)
In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
, the class for logspace problems on a deterministic Turing machine. Since any deterministic Turing machine is also a nondeterministic Turing machine, we have that L is contained in NL.
NL can be formally defined in terms of the computational resource nondeterministic space (or NSPACE) as NL = NSPACE(log n).
Important results in complexity theory allow us to relate this complexity class with other classes, telling us about the relative power of the resources involved. Results in the field of algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s, on the other hand, tell us which problems can be solved with this resource. Unfortunately, like much of complexity theory, many important questions about NL are still open
Open problem
In science and mathematics, an open problem or an open question is a known problem that can be accurately stated, and has not yet been solved . Some questions remain unanswered for centuries before solutions are found...
(see Unsolved problems in computer science).
Occasionally NL is referred to as RL due to its probabilistic definition below; however, this name is more frequently used to refer to randomized logarithmic space, which is not known to equal NL.
NL-complete problems
Several problems are known to be NL-completeNL-complete
In computational complexity theory, NL-Complete is a complexity class which is complete for NL. It contains the most "difficult" or "expressive" problems in NL...
under log-space reduction
Log-space reduction
In computational complexity theory, a log-space reduction is a reduction computable by a deterministic Turing machine using logarithmic space. Conceptually, this means it can keep a constant number of pointers into the input, along with a logarithmic number of fixed-size integers...
s, including ST-connectivity
ST-connectivity
In computer science and computational complexity theory, st-connectivity or STCON is a decision problem asking, for vertices s and t in a directed graph, if t is reachable from s.Formally, the decision problem is given by- Complexity :...
and 2-satisfiability
2-satisfiability
In computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...
. ST-connectivity
ST-connectivity
In computer science and computational complexity theory, st-connectivity or STCON is a decision problem asking, for vertices s and t in a directed graph, if t is reachable from s.Formally, the decision problem is given by- Complexity :...
asks for nodes S and T in a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
whether T is reachable
Reachability
In graph theory, reachability is the notion of being able to get from one vertex in a directed graph to some other vertex. Note that reachability in undirected graphs is trivial — it is sufficient to find the connected components in the graph, which can be done in linear time.- Definition :For a...
from S. 2-satisfiability
2-satisfiability
In computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...
asks, given a formula of which each clause is the disjunction of two literals, if there is a variable assignment that makes the formula true. An example instance, where ~ indicates not, might be:
and (~x2 or x3) and (~x1 or ~x2)
Containments
It is known that NL is contained in PP (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
, since there is a polynomial-time algorithm for 2-satisfiability
2-satisfiability
In computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...
, but it is not known whether NL = P or whether L = NL. It is known that NL = co-NL, where co-NL is the complement
Complement (complexity)
In computational complexity theory, the complement of a decision problem is the decision problem resulting from reversing the yes and no answers. Equivalently, if we define decision problems as sets of finite strings, then the complement of this set over some fixed domain is its complement...
of NL. This result was independently discovered by Neil Immerman
Neil Immerman
Neil Immerman is an American theoretical computer scientist, a professor of computer science at the University of Massachusetts Amherst...
and Róbert Szelepcsényi
Róbert Szelepcsényi
Róbert Szelepcsényi was a Slovak student of Hungarian descent and a member of the Faculty of Mathematics, Physics and Informatics of Comenius University in Bratislava....
in 1987 (Immerman-Szelepcsényi Theorem
Immerman-Szelepcsényi theorem
In computational complexity theory, the Immerman–Szelepcsényi theorem was proven independently by Neil Immerman and Róbert Szelepcsényi in 1987, for which they shared the 1995 Gödel Prize. In its general form the theorem states that NSPACE = co-NSPACE for any function s ≥ log n...
), who received the 1995 Gödel Prize
Gödel Prize
The Gödel Prize is a prize for outstanding papers in theoretical computer science, named after Kurt Gödel and awarded jointly by the European Association for Theoretical Computer Science and the Association for Computing Machinery Special Interest Group on Algorithms and Computation Theory .The...
for this work.
In circuit complexity
Circuit complexity
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of Boolean circuits that compute them....
, NL can be placed within the NC
NC (complexity)
In complexity theory, the class NC is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem is in NC if there exist constants c and k such that it can be solved in time O using O parallel processors...
hierarchy. In Papadimitriou 1994, Theorem 16.1, we have:
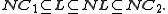
More precisely, NL is contained in AC1
AC (complexity)
In circuit complexity, AC is a complexity class hierarchy. Each class, ACi, consists of the languages recognized by Boolean circuits with depth O and a polynomial number of unlimited-fanin AND and OR gates....
. It is known that NL is equal to ZPL, the class of problems solvable by randomized algorithms in logarithmic space and unbounded time, with no error. It is not, however, known or believed to be equal to RLP or ZPLP, the polynomial-time restrictions of RL and ZPL which some authors refer to as RL and ZPL.
We can relate NL to deterministic space using Savitch's theorem
Savitch's theorem
In computational complexity theory, Savitch's theorem, proved by Walter Savitch in 1970, states that for any function ƒ ≥ log,...
, which tells us that any nondeterministic algorithm can be simulated by a deterministic machine in at most quadratically more space. From Savitch's theorem, we have directly that:
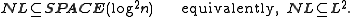
This was the strongest deterministic-space inclusion known (Papadimitriou 1994 Problem 16.4.10, "Symmetric space"). Since larger space classes are not affected by quadratic increases, the nondeterministic and deterministic classes are known to be equal, so that for example we have PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
= NPSPACE.
Probabilistic definition
Suppose C is the complexity classComplexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
of problems solvable in logarithmithic space with probabilistic Turing machine
Probabilistic Turing machine
In computability theory, a probabilistic Turing machine is a non-deterministic Turing machine which randomly chooses between the available transitions at each point according to some probability distribution....
s that never accept incorrectly but are allowed to reject incorrectly less than 1/3 of the time; this is called one-sided error. The constant 1/3 is arbitrary; any x with 0 ≤ x < 1/2 would suffice.
It turns out that C = NL. Notice that C, unlike its deterministic counterpart L
L (complexity)
In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
, is not limited to polynomial time, because although it has a polynomial number of configurations it can use randomness to escape an infinite loop. If we do limit it to polynomial time, we get the class RL, which is contained in but not known or believed to equal NL.
There is a simple algorithm which establishes that C = NL. Clearly C is contained in NL, since:
- If the string is not in the language, both reject along all computation paths.
- If the string is in the language, an NL algorithm accepts along at least one computation path and a C algorithm accepts along at least two-thirds of its computation paths.
To show that NL is contained in C, we simply take an NL algorithm and choose a random computation path of length n, and do this 2n times. Because no computation path exceeds length n, and because there are 2n computation paths in all, we have a good chance of hitting the accepting one (bounded below by a constant).
The only problem is that we don't have room in log space for a binary counter that goes up to 2n. To get around this we replace it with a randomized counter, which simply flips n coins and stops and rejects if they all land on heads. Since this event has probability 2-n, we expect
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
to take 2n steps on average before stopping. It only needs to keep a running total of the number of heads in a row it sees, which it can count in log space.
Thus, when we only look at space alone, it seems that randomization and nondeterminism are equally powerful.
Descriptive complexity
There is a simple logical characterization of NL: it contains precisely those languages expressible in first-order logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
with an added transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
operator.

