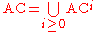AC (complexity)
Encyclopedia
In circuit complexity
, AC is a complexity class
hierarchy. Each class, ACi, consists of the languages
recognized by Boolean circuit
s with depth and a polynomial number
and a polynomial number
of unlimited-fanin AND
and OR gate
s.
The name "AC" was chosen by analogy to NC
, with the "A" in the name standing for "alternating" and referring both to the alternation between the AND and OR gates in the circuits and to alternating Turing machine
s.
The smallest AC class is AC0
, consisting of constant-depth unlimited-fanin circuits.
The total hierarchy of AC classes is defined as
classes, which are defined similarly, but with gates having only constant fanin. For each i, we have
As an immediate consequence of this, we have that NC = AC.
for some modulus m, we have the classes ACCi[m
].
Circuit complexity
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of Boolean circuits that compute them....
, AC is a complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
hierarchy. Each class, ACi, consists of the languages
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
recognized by Boolean circuit
Boolean circuit
A Boolean circuit is a mathematical model of computation used in studying computational complexity theory. Boolean circuits are the main object of study in circuit complexity and are a special kind of circuits; a formal language can be decided by a family of Boolean circuits, one circuit for each...
s with depth
 and a polynomial number
and a polynomial numberPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of unlimited-fanin AND
AND gate
The AND gate is a basic digital logic gate that implements logical conjunction - it behaves according to the truth table to the right. A HIGH output results only if both the inputs to the AND gate are HIGH . If neither or only one input to the AND gate is HIGH, a LOW output results...
and OR gate
OR gate
The OR gate is a digital logic gate that implements logical disjunction - it behaves according to the truth table to the right. A HIGH output results if one or both the inputs to the gate are HIGH . If neither input is HIGH, a LOW output results...
s.
The name "AC" was chosen by analogy to NC
NC (complexity)
In complexity theory, the class NC is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem is in NC if there exist constants c and k such that it can be solved in time O using O parallel processors...
, with the "A" in the name standing for "alternating" and referring both to the alternation between the AND and OR gates in the circuits and to alternating Turing machine
Alternating Turing machine
In computational complexity theory, an alternating Turing machine is a non-deterministic Turing machine with a rule for accepting computations that generalizes the rules used in the definition of the complexity classes NP and co-NP...
s.
The smallest AC class is AC0
AC0
AC0 is a complexity class used in circuit complexity. It is the smallest class in the AC hierarchy, and consists of all families of circuits of depth O and polynomial size, with unlimited-fanin AND gates and OR gates....
, consisting of constant-depth unlimited-fanin circuits.
The total hierarchy of AC classes is defined as
Relation to NC
The AC classes are related to the NCNC (complexity)
In complexity theory, the class NC is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem is in NC if there exist constants c and k such that it can be solved in time O using O parallel processors...
classes, which are defined similarly, but with gates having only constant fanin. For each i, we have

As an immediate consequence of this, we have that NC = AC.
Variations
The power of the AC classes can be affected by adding additional gates. If we add gates which calculate the modulo operationModulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
for some modulus m, we have the classes ACCi[m
ACC (complexity)
ACC0, sometimes called ACC, is a class of computational models and problems defined in circuit complexity, a field of theoretical computer science. The class is defined as by augmenting the class AC0 of "alternating circuits" with the ability to count; the acronym ACC stands for "AC with counters"...
].