
PSPACE
Encyclopedia
In computational complexity theory
, PSPACE is the set of all decision problem
s which can be solved by a Turing machine using a polynomial
amount of space.
 , the set of all problems that can be solved by Turing machines using at most
, the set of all problems that can be solved by Turing machines using at most 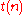 space for some function
space for some function  of the input size
of the input size  , then we can define PSPACE formally as
, then we can define PSPACE formally as
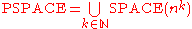
PSPACE is a strict superset of the set of context-sensitive language
s.
It turns out that allowing the Turing machine to be nondeterministic
does not add any extra power. Because of Savitch's theorem
, NPSPACE is equivalent to PSPACE, essentially because a deterministic Turing machine can simulate a nondeterministic Turing machine without needing much more space (even though it may use much more time). Also, the complements
of all problems in PSPACE are also in PSPACE, meaning that Co-PSPACE = PSPACE.
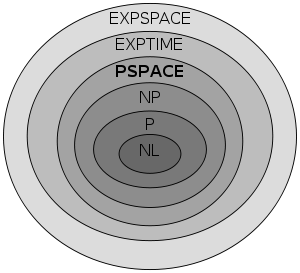 The following relations are known between PSPACE and the complexity classes NL
The following relations are known between PSPACE and the complexity classes NL
, P
, NP
, PH, EXPTIME
and EXPSPACE
(note that is not
is not 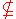 ):
):


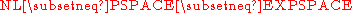
It is known that in the first and second line, at least one of the set containments must be strict, but it is not known which. It is widely suspected that all are strict.
The containments in the third line are both known to be strict. The first follows from direct diagonalization (the space hierarchy theorem
,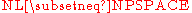 ) and the fact that
) and the fact that  via Savitch's theorem
via Savitch's theorem
. The second follows simply from the space hierarchy theorem.
The hardest problems in PSPACE are the PSPACE-Complete problems. See PSPACE-Complete
for examples of problems that are suspected to be in PSPACE but not in NP.
in polynomial time, sometimes called APTIME or just AP.
A logical characterization of PSPACE from descriptive complexity
theory is that it is the set of problems expressible in second-order logic
with the addition of a transitive closure
operator. A full transitive closure is not needed; a commutative transitive closure and even weaker forms suffice. It is the addition of this operator that (possibly) distinguishes PSPACE from PH.
A major result of complexity theory is that PSPACE can be characterized as all the languages recognizable by a particular interactive proof system
, the one defining the class IP
. In this system, there is an all-powerful prover trying to convince a randomized polynomial-time verifier that a string is in the language. It should be able to convince the verifier with high probability if the string is in the language, but should not be able to convince it except with low probability if the string is not in the language.
PSPACE can be characterized as the quantum complexity class QIP.
if it is in PSPACE and it is PSPACE-hard, which means for all A PSPACE, A
PSPACE, A 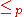 B, where A
B, where A 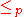 B means that there is a polynomial-time many-one reduction from A to B. PSPACE-complete problems are of great importance to studying PSPACE problems because they represent the most difficult problems in PSPACE. Finding a simple solution to a PSPACE-complete problem would mean we have a simple solution to all other problems in PSPACE because all PSPACE problems could be reduced to a PSPACE-complete problem. A problem can be PSPACE-hard but not PSPACE-complete because it may not be in PSPACE. For example, the halting problem
B means that there is a polynomial-time many-one reduction from A to B. PSPACE-complete problems are of great importance to studying PSPACE problems because they represent the most difficult problems in PSPACE. Finding a simple solution to a PSPACE-complete problem would mean we have a simple solution to all other problems in PSPACE because all PSPACE problems could be reduced to a PSPACE-complete problem. A problem can be PSPACE-hard but not PSPACE-complete because it may not be in PSPACE. For example, the halting problem
is PSPACE-hard, but not PSPACE-complete.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, PSPACE is the set of all decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s which can be solved by a Turing machine using a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
amount of space.
Formal definition
If we denote by , the set of all problems that can be solved by Turing machines using at most
, the set of all problems that can be solved by Turing machines using at most 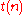 space for some function
space for some function  of the input size
of the input size  , then we can define PSPACE formally as
, then we can define PSPACE formally as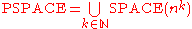
PSPACE is a strict superset of the set of context-sensitive language
Context-sensitive language
In theoretical computer science, a context-sensitive language is a formal language that can be defined by a context-sensitive grammar. That is one of the four types of grammars in the Chomsky hierarchy...
s.
It turns out that allowing the Turing machine to be nondeterministic
Nondeterministic algorithm
In computer science, a nondeterministic algorithm is an algorithm that can exhibit different behaviors on different runs, as opposed to a deterministic algorithm. There are several ways an algorithm may behave differently from run to run. A concurrent algorithm can perform differently on different...
does not add any extra power. Because of Savitch's theorem
Savitch's theorem
In computational complexity theory, Savitch's theorem, proved by Walter Savitch in 1970, states that for any function ƒ ≥ log,...
, NPSPACE is equivalent to PSPACE, essentially because a deterministic Turing machine can simulate a nondeterministic Turing machine without needing much more space (even though it may use much more time). Also, the complements
Complement (complexity)
In computational complexity theory, the complement of a decision problem is the decision problem resulting from reversing the yes and no answers. Equivalently, if we define decision problems as sets of finite strings, then the complement of this set over some fixed domain is its complement...
of all problems in PSPACE are also in PSPACE, meaning that Co-PSPACE = PSPACE.
Relation among other classes

NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
, P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
, NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, PH, EXPTIME
EXPTIME
In computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
and EXPSPACE
EXPSPACE
In complexity theory, EXPSPACE is the set of all decision problems solvable by a deterministic Turing machine in O space, where p is a polynomial function of n...
(note that
 is not
is not 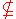 ):
):

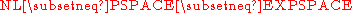
It is known that in the first and second line, at least one of the set containments must be strict, but it is not known which. It is widely suspected that all are strict.
The containments in the third line are both known to be strict. The first follows from direct diagonalization (the space hierarchy theorem
Space hierarchy theorem
In computational complexity theory, the space hierarchy theorems are separation results that show that both deterministic and nondeterministic machines can solve more problems in more space, subject to certain conditions. For example, a deterministic Turing machine can solve more decision problems...
,
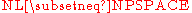 ) and the fact that
) and the fact that  via Savitch's theorem
via Savitch's theoremSavitch's theorem
In computational complexity theory, Savitch's theorem, proved by Walter Savitch in 1970, states that for any function ƒ ≥ log,...
. The second follows simply from the space hierarchy theorem.
The hardest problems in PSPACE are the PSPACE-Complete problems. See PSPACE-Complete
PSPACE-complete
In complexity theory, a decision problem is PSPACE-complete if it is in the complexity class PSPACE, and every problem in PSPACE can be reduced to it in polynomial time...
for examples of problems that are suspected to be in PSPACE but not in NP.
Other characterizations
An alternative characterization of PSPACE is the set of problems decidable by an alternating Turing machineAlternating Turing machine
In computational complexity theory, an alternating Turing machine is a non-deterministic Turing machine with a rule for accepting computations that generalizes the rules used in the definition of the complexity classes NP and co-NP...
in polynomial time, sometimes called APTIME or just AP.
A logical characterization of PSPACE from descriptive complexity
Descriptive complexity
Descriptive complexity is a branch of computational complexity theory and of finite model theory that characterizes complexity classes by the type of logic needed to express the languages in them. For example, PH, the union of all complexity classes in the polynomial hierarchy, is precisely the...
theory is that it is the set of problems expressible in second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
with the addition of a transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
operator. A full transitive closure is not needed; a commutative transitive closure and even weaker forms suffice. It is the addition of this operator that (possibly) distinguishes PSPACE from PH.
A major result of complexity theory is that PSPACE can be characterized as all the languages recognizable by a particular interactive proof system
Interactive proof system
In computational complexity theory, an interactive proof system is an abstract machine that models computation as the exchange of messages between two parties. The parties, the verifier and the prover, interact by exchanging messages in order to ascertain whether a given string belongs to a...
, the one defining the class IP
IP (complexity)
In computational complexity theory, the class IP is the class of problems solvable by an interactive proof system. The concept of an interactive proof system was first introduced by Shafi Goldwasser, Silvio Micali, and Charles Rackoff in 1985...
. In this system, there is an all-powerful prover trying to convince a randomized polynomial-time verifier that a string is in the language. It should be able to convince the verifier with high probability if the string is in the language, but should not be able to convince it except with low probability if the string is not in the language.
PSPACE can be characterized as the quantum complexity class QIP.
PSPACE-completeness
A language B is PSPACE-completePSPACE-complete
In complexity theory, a decision problem is PSPACE-complete if it is in the complexity class PSPACE, and every problem in PSPACE can be reduced to it in polynomial time...
if it is in PSPACE and it is PSPACE-hard, which means for all A
 PSPACE, A
PSPACE, A 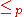 B, where A
B, where A 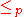 B means that there is a polynomial-time many-one reduction from A to B. PSPACE-complete problems are of great importance to studying PSPACE problems because they represent the most difficult problems in PSPACE. Finding a simple solution to a PSPACE-complete problem would mean we have a simple solution to all other problems in PSPACE because all PSPACE problems could be reduced to a PSPACE-complete problem. A problem can be PSPACE-hard but not PSPACE-complete because it may not be in PSPACE. For example, the halting problem
B means that there is a polynomial-time many-one reduction from A to B. PSPACE-complete problems are of great importance to studying PSPACE problems because they represent the most difficult problems in PSPACE. Finding a simple solution to a PSPACE-complete problem would mean we have a simple solution to all other problems in PSPACE because all PSPACE problems could be reduced to a PSPACE-complete problem. A problem can be PSPACE-hard but not PSPACE-complete because it may not be in PSPACE. For example, the halting problemHalting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
is PSPACE-hard, but not PSPACE-complete.

