Immerman-Szelepcsényi theorem
Encyclopedia
In computational complexity theory
, the Immerman–Szelepcsényi theorem was proven independently by Neil Immerman
and Róbert Szelepcsényi
in 1987, for which they shared the 1995 Gödel Prize
. In its general form the theorem states that NSPACE
(s(n)) = co-NSPACE(s(n)) for any function s(n) ≥ log n. The result is equivalently stated as NL
= co-NL, although this is the special case when s(n) = log n, it implies the general theorem by a standard padding argument
. The result solved the second LBA problem.
In other words, if a nondeterministic machine can solve a problem, it can solve its complement
problem (with the yes and no answers reversed) in the same asymptotic amount of space. No similar result is known for the time complexity classes, and indeed it is conjectured that NP
is not equal to co-NP.
The first step is to demonstrate that NL
= co-NL. This can be accomplished by taking the st-connectivity
problem (known to be NL-complete
), and showing that the complement of this problem (called st-non-connectivity) is also in NL.
Definition: Given a directed graph
G with n vertices, and vertices s and t in G, the st-non-connectivity problem is to determine whether there is no directed path
between vertex s and t:
In order to illustrate that st-non-connectivity is in NL, one can construct a non-deterministic algorithm that, in logarithmic space, decides whether two given vertices are not connected. To prove correctness of this algorithm, one must show two things:
Here are the key ideas of the proof of the second condition. For sake of contradiction assume that s and t are connected but the algorithm accepts. To keep the adversary controlling the non-determinism "honest", the algorithm is designed so that if the non-determinism is uncooperative, the algorithm rejects at the end of the ENUMERATE subroutine. Therefore since we assumed that the algorithm accepts, the non-determinism must have been cooperative, which implies by the design of the algorithm that we should have rejected, a contradiction.
First, define Ai as follows:
Ai = {v: there is a path from s to v of length ≤ i}. In other words, Ai will include all vertices that are reachable from s in i or
fewer hops. Let ri = |Ai|. Note that if t is not in An−1, where n = |V|, then there is no path from s to t in G, i.e.,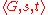
∈ st-non-connectivity.
Lemma: An algorithm can be constructed that given ri will enumerate vertices in Ai and ACCEPT in logarithmic space. Note that if the given ri is larger than the true number of vertices in Ai, then the algorithm REJECTs; however, if ri is less than the true number of vertices in Ai the algorithm would ACCEPT but enumerate only a subset of Ai.
ENUMERATE(s,i,r_i,G)
1: Counter := 0
2: FOR ALL vertices v in G
3: Nondeterministically either CONTINUE or guess a path of length less than or equal to i from s to v
4: Counter := Counter + 1
5: Output v
6: IF Counter ≥ r_i
7: ACCEPT
8: REJECT
ENUMERATE goes through all vertices of graph G in logarithmic space, since the representation of each vertex and the Counter requires only log |G| bits and nondeterministically selecting a path also requires only logarithmic space.
Now, with ENUMERATE at hand it is possible to compute the actual ri in log-space using an algorithm that is based on the principle of mathematical induction
. When using ENUMERATE as a subroutine, replace ACCEPT in ENUMERATE with RETURN while leaving REJECT as REJECT.
Obviously r0 = 1 since Ai includes only the vertex s itself.
Now, assume ri is given. Then ri+1 can be calculated by the following algorithm in log-space:
INDUCTIVE-COUNTING (s,i,r_i,G)
1: r := 1
2: FOR ALL vertices v ≠ s:
3: FOR EACH u such that (u,v) is an edge in G
4: ENUMERATE (s,i,r_i,G)
5: IF u is ever output
6: r := r + 1
7: BREAK
8: Output r
This algorithm first accounts for the initial vertex s, and then goes through all other vertices v of the graph G. In lines 3–6 the algorithm tries to find a vertex u in Ai directly connected to the vertex v by simulating ENUMERATE. If such vertex is found, that means that v is in Ai+1, so the result is incremented to account for this vertex. Note that the algorithm does not need to store all of the output of ENUMERATE every time it is called as a sub-routine. It can only store one vertex at a time and check if u is ever output. Thus, this algorithm runs in logarithmic space.
With this algorithm at hand we can devise an algorithm for st-non-connectivity consisting of two parts. The first part would compute rn by starting with r0 = 1 and then using INDUCTIVE-COUNTING n − 1 times. In the second part the algorithm just simulates ENUMERATE with the computed rn and if t is ever output that means it can be reached from v, and the algorithm REJECTs.
NOT-CONNECTED (G,s,t)
1: r_n := 1;
2: FOR i := 1 TO n
3: r_n := INDUCTIVE-COUNTING (s,i,r_n,G)
4: ENUMERATE (s,n,r_n,G)
5: IF t is ever output
6: REJECT
8: ELSE
9: ACCEPT
This algorithm runs in logarithmic space, since we need log |G| bits for storing i and rn. As was shown above, the ENUMERATE and INDUCTIVE-COUNTING algorithms also run in logarithmic space and again we do not need to store all of the output of ENUMERATE in line 4, but need only to check if t is ever output. Thus, NOT-CONNECTED can decide if there exists no path from vertex s to t in logarithmic space. I.e., st-non-connectivity is in NL. Since we can reduce each problem in NL to st-connectivity and each problem in co-NL to st-non-connectivity we conclude that NL = co-NL.
Now, for s(n) ≥ log n we can transform the computations of any non-deterministic Turing machine
M on language L into a graph of its states and simulate M using st-connectivity algorithm. Analogously we can transform any co-language into st-non-connectivity problem.
Both of these graphs would have 2O(s(n)) vertices if L ∈ NSPACE(s(n)). Thus, we can decide both reachability and non-reachability of the ACCEPT state in log(2O(s(n))) = O(s(n)) space and NSPACE(s(n)) = co-NSPACE(s(n)).
's equality between NL
and FO(Transitive Closure), the logarithmic hierarchy, i.e. the languages decided by alternating Turing machine
in logarithm space with a bounded number of alternation, is the same class as NL.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, the Immerman–Szelepcsényi theorem was proven independently by Neil Immerman
Neil Immerman
Neil Immerman is an American theoretical computer scientist, a professor of computer science at the University of Massachusetts Amherst...
and Róbert Szelepcsényi
Róbert Szelepcsényi
Róbert Szelepcsényi was a Slovak student of Hungarian descent and a member of the Faculty of Mathematics, Physics and Informatics of Comenius University in Bratislava....
in 1987, for which they shared the 1995 Gödel Prize
Gödel Prize
The Gödel Prize is a prize for outstanding papers in theoretical computer science, named after Kurt Gödel and awarded jointly by the European Association for Theoretical Computer Science and the Association for Computing Machinery Special Interest Group on Algorithms and Computation Theory .The...
. In its general form the theorem states that NSPACE
NSPACE
In computational complexity theory, the complexity class NSPACE is the set of decision problems that can be solved by a non-deterministic Turing machine using space O, and unlimited time. It is the non-deterministic counterpart of DSPACE.Several important complexity classes can be defined in terms...
(s(n)) = co-NSPACE(s(n)) for any function s(n) ≥ log n. The result is equivalently stated as NL
NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
= co-NL, although this is the special case when s(n) = log n, it implies the general theorem by a standard padding argument
Padding argument
In computational complexity theory, the padding argument is a tool to conditionally prove that if some complexity classes are equal, then some other bigger classes are also equal.- Example :If P is equal to NP then EXP is equal to NEXP...
. The result solved the second LBA problem.
In other words, if a nondeterministic machine can solve a problem, it can solve its complement
Complement (complexity)
In computational complexity theory, the complement of a decision problem is the decision problem resulting from reversing the yes and no answers. Equivalently, if we define decision problems as sets of finite strings, then the complement of this set over some fixed domain is its complement...
problem (with the yes and no answers reversed) in the same asymptotic amount of space. No similar result is known for the time complexity classes, and indeed it is conjectured that NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
is not equal to co-NP.
Proof
Theorem: Let s(n) ≥ log n be any function. Then NSPACE[s(n)] = co-NSPACE[s(n)].The first step is to demonstrate that NL
NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
= co-NL. This can be accomplished by taking the st-connectivity
ST-connectivity
In computer science and computational complexity theory, st-connectivity or STCON is a decision problem asking, for vertices s and t in a directed graph, if t is reachable from s.Formally, the decision problem is given by- Complexity :...
problem (known to be NL-complete
NL-complete
In computational complexity theory, NL-Complete is a complexity class which is complete for NL. It contains the most "difficult" or "expressive" problems in NL...
), and showing that the complement of this problem (called st-non-connectivity) is also in NL.
Definition: Given a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
G with n vertices, and vertices s and t in G, the st-non-connectivity problem is to determine whether there is no directed path
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
between vertex s and t:
In order to illustrate that st-non-connectivity is in NL, one can construct a non-deterministic algorithm that, in logarithmic space, decides whether two given vertices are not connected. To prove correctness of this algorithm, one must show two things:
- If the non-deterministic choices are made "correctly" and s and t are disconnected, then the algorithm accepts.
- If s and t are connected, no matter what non-deterministic choices are made the algorithm does not accept.
Here are the key ideas of the proof of the second condition. For sake of contradiction assume that s and t are connected but the algorithm accepts. To keep the adversary controlling the non-determinism "honest", the algorithm is designed so that if the non-determinism is uncooperative, the algorithm rejects at the end of the ENUMERATE subroutine. Therefore since we assumed that the algorithm accepts, the non-determinism must have been cooperative, which implies by the design of the algorithm that we should have rejected, a contradiction.
First, define Ai as follows:
Ai = {v: there is a path from s to v of length ≤ i}. In other words, Ai will include all vertices that are reachable from s in i or
fewer hops. Let ri = |Ai|. Note that if t is not in An−1, where n = |V|, then there is no path from s to t in G, i.e.,
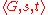∈ st-non-connectivity.Lemma: An algorithm can be constructed that given ri will enumerate vertices in Ai and ACCEPT in logarithmic space. Note that if the given ri is larger than the true number of vertices in Ai, then the algorithm REJECTs; however, if ri is less than the true number of vertices in Ai the algorithm would ACCEPT but enumerate only a subset of Ai.
ENUMERATE(s,i,r_i,G)
1: Counter := 0
2: FOR ALL vertices v in G
3: Nondeterministically either CONTINUE or guess a path of length less than or equal to i from s to v
4: Counter := Counter + 1
5: Output v
6: IF Counter ≥ r_i
7: ACCEPT
8: REJECT
ENUMERATE goes through all vertices of graph G in logarithmic space, since the representation of each vertex and the Counter requires only log |G| bits and nondeterministically selecting a path also requires only logarithmic space.
Now, with ENUMERATE at hand it is possible to compute the actual ri in log-space using an algorithm that is based on the principle of mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. When using ENUMERATE as a subroutine, replace ACCEPT in ENUMERATE with RETURN while leaving REJECT as REJECT.
Obviously r0 = 1 since Ai includes only the vertex s itself.
Now, assume ri is given. Then ri+1 can be calculated by the following algorithm in log-space:
INDUCTIVE-COUNTING (s,i,r_i,G)
1: r := 1
2: FOR ALL vertices v ≠ s:
3: FOR EACH u such that (u,v) is an edge in G
4: ENUMERATE (s,i,r_i,G)
5: IF u is ever output
6: r := r + 1
7: BREAK
8: Output r
This algorithm first accounts for the initial vertex s, and then goes through all other vertices v of the graph G. In lines 3–6 the algorithm tries to find a vertex u in Ai directly connected to the vertex v by simulating ENUMERATE. If such vertex is found, that means that v is in Ai+1, so the result is incremented to account for this vertex. Note that the algorithm does not need to store all of the output of ENUMERATE every time it is called as a sub-routine. It can only store one vertex at a time and check if u is ever output. Thus, this algorithm runs in logarithmic space.
With this algorithm at hand we can devise an algorithm for st-non-connectivity consisting of two parts. The first part would compute rn by starting with r0 = 1 and then using INDUCTIVE-COUNTING n − 1 times. In the second part the algorithm just simulates ENUMERATE with the computed rn and if t is ever output that means it can be reached from v, and the algorithm REJECTs.
NOT-CONNECTED (G,s,t)
1: r_n := 1;
2: FOR i := 1 TO n
3: r_n := INDUCTIVE-COUNTING (s,i,r_n,G)
4: ENUMERATE (s,n,r_n,G)
5: IF t is ever output
6: REJECT
8: ELSE
9: ACCEPT
This algorithm runs in logarithmic space, since we need log |G| bits for storing i and rn. As was shown above, the ENUMERATE and INDUCTIVE-COUNTING algorithms also run in logarithmic space and again we do not need to store all of the output of ENUMERATE in line 4, but need only to check if t is ever output. Thus, NOT-CONNECTED can decide if there exists no path from vertex s to t in logarithmic space. I.e., st-non-connectivity is in NL. Since we can reduce each problem in NL to st-connectivity and each problem in co-NL to st-non-connectivity we conclude that NL = co-NL.
Now, for s(n) ≥ log n we can transform the computations of any non-deterministic Turing machine
Non-deterministic Turing machine
In theoretical computer science, a Turing machine is a theoretical machine that is used in thought experiments to examine the abilities and limitations of computers....
M on language L into a graph of its states and simulate M using st-connectivity algorithm. Analogously we can transform any co-language into st-non-connectivity problem.
Both of these graphs would have 2O(s(n)) vertices if L ∈ NSPACE(s(n)). Thus, we can decide both reachability and non-reachability of the ACCEPT state in log(2O(s(n))) = O(s(n)) space and NSPACE(s(n)) = co-NSPACE(s(n)).
Logspace hierarchy
As a corollary, in the same article, Immerman proved that, using descriptive complexityDescriptive complexity
Descriptive complexity is a branch of computational complexity theory and of finite model theory that characterizes complexity classes by the type of logic needed to express the languages in them. For example, PH, the union of all complexity classes in the polynomial hierarchy, is precisely the...
's equality between NL
NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
and FO(Transitive Closure), the logarithmic hierarchy, i.e. the languages decided by alternating Turing machine
Alternating Turing machine
In computational complexity theory, an alternating Turing machine is a non-deterministic Turing machine with a rule for accepting computations that generalizes the rules used in the definition of the complexity classes NP and co-NP...
in logarithm space with a bounded number of alternation, is the same class as NL.
See also
- Savitch's theoremSavitch's theoremIn computational complexity theory, Savitch's theorem, proved by Walter Savitch in 1970, states that for any function ƒ ≥ log,...
relates nondeterministic space classes to their deterministic counterparts
External links
- Lance Fortnow, Foundations of Complexity, Lesson 19: The Immerman–Szelepcsenyi Theorem. Accessed 09/09/09.