Mutual fund separation theorem
Encyclopedia
In portfolio theory
, a mutual fund separation theorem, mutual fund theorem, or separation theorem is a theorem
stating that, under certain conditions, any investor's optimal portfolio can be constructed by holding each of certain mutual fund
s in appropriate ratios, where the number of mutual funds is smaller than the number of individual assets in the portfolio. Here a mutual fund refers to any specified benchmark portfolio of the available assets. There are two advantages of having a mutual fund theorem. First, if the relevant conditions are met, it may be easier (or lower in transactions costs) for an investor to purchase a smaller number of mutual funds than to purchase a larger number of assets individually. Second, from a theoretical and empirical standpoint, if it can be assumed that the relevant conditions are indeed satisfied, then implications
for the functioning of asset markets can be derived and tested.
consistent with that investor's chosen level of expected return
(called a mean-variance efficient portfolio), if the returns on the assets are jointly elliptically distributed
, including the special case in which they are jointly normally distributed. Under mean-variance analysis, it can be shown that every variance-minimizing portfolio given a particular expected return (that is, every efficient portfolio) can be formed as a combination of any two efficient portfolios. If the investor's optimal portfolio has an expected return that is between the expected returns on two efficient benchmark portfolios, then that investor's portfolio can be characterized as consisting of positive quantities of the two benchmark portfolios.
, let
be the variance of the portfolio return, let 
be the level of expected return on the portfolio that portfolio return variance is to be minimized contingent upon, let 
be the vector of expected returns on the available assets, let 
be the vector of amounts to be placed in the available assets, let 
be the amount of wealth that is to be allocated in the portfolio, and let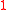 
be a vector of ones. Then the problem of minimizing the portfolio return variance subject to a given level of expected portfolio return can be stated as
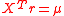
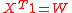
where the superscript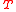
denotes the transpose
of a matrix. The portfolio return variance in the objective function can be written as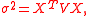
where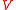 
is the positive definite covariance matrix
of the individual assets' returns. The Lagrangian
for this constrained optimization problem (whose second-order conditions can be shown to be satisfied) is
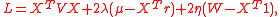
with Lagrange multipliers
and 
.This can be solved for the optimal vector 
of asset quantities by equating to zero the derivatives
with respect to
, 
, and 
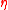, provisionally solving the first-order condition for 
in terms of 
and 
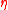, substituting into the other first-order conditions, solving for 
and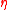 
in terms of the model parameters, and substituting back into the provisional solution for 
. The result is
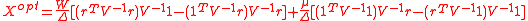
where
For simplicity this can be written more compactly as
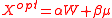
where
and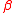 
are parameter vectors based on the underlying model parameters. Now consider two benchmark efficient portfolios constructed at benchmark expected returns 
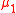and 
and thus given by
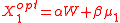
and
The optimal portfolio at arbitrary
can then be written as a weighted average of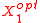 
and 
as follows:
This equation proves the two-fund separation theorem for mean-variance analysis. For a geometric interpretation, see the Markowitz bullet.
is available, then again a two-fund separation theorem applies; but in this case one of the "funds" can be chosen to be a very simple fund containing only the risk-free asset, and the other fund can be chosen to be one which contains zero holdings of the risk-free asset. (With the risk-free asset referred to as "money", this form of the theorem is referred to as the monetary separation theorem.) Thus mean-variance efficient portfolios can be formed simply as a combination of holdings of the risk-free asset and holdings of a particular efficient fund that contains only risky assets. The derivation above does not apply, however, since with a risk-free asset the above covariance matrix of all asset returns,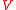
, would have one row and one column of zeroes and thus would not be invertible. Instead, the problem can be set up as
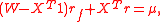
where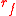
is the known return on the risk-free asset, X is now the vector of quantities to be held in the risky assets, and 
is the vector of expected returns on the risky assets. The left side of the last equation is the expected return on the portfolio, since 
is the quantity held in the risk-free asset, thus incorporating the asset adding-up constraint that in the earlier problem required the inclusion of a separate Lagrangian constraint. The objective function can be written as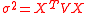 
, where now 
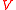is the covariance matrix of the risky assets only. This optimization problem can be shown to yield the optimal vector of risky asset holdings
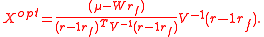
Of course this equals a zero vector if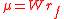
, the risk-free portfolio's return, in which case all wealth is held in the risk-free asset. It can be shown that the portfolio with exactly zero holdings of the risk-free asset occurs at 
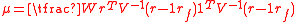and is given by
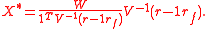
It can also be shown (analogously to the demonstration in the above two-mutual-fund case) that every portfolio's risky asset vector (that is,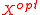
for every value of 
) can be formed as a weighted combination of the latter vector and the zero vector. For a geometric interpretation, see the efficient frontier with no risk-free asset.
(HARA) (such as is true for the power utility function and the exponential utility function
) , separation theorems can be obtained without the use of mean-variance analysis. For example, David Cass
and Joseph Stiglitz showed in 1970 that two-fund monetary separation applies if all investors have HARA utility with the same exponent as each other.
More recently, in the dynamic portfolio optimization model of Çanakoğlu and Özekici, the investor's level of initial wealth (the distinguishing feature of investors) does not affect the optimal composition of the risky part of the portfolio. A similar result is given by Schmedders.
Modern portfolio theory
Modern portfolio theory is a theory of investment which attempts to maximize portfolio expected return for a given amount of portfolio risk, or equivalently minimize risk for a given level of expected return, by carefully choosing the proportions of various assets...
, a mutual fund separation theorem, mutual fund theorem, or separation theorem is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
stating that, under certain conditions, any investor's optimal portfolio can be constructed by holding each of certain mutual fund
Mutual fund
A mutual fund is a professionally managed type of collective investment scheme that pools money from many investors to buy stocks, bonds, short-term money market instruments, and/or other securities.- Overview :...
s in appropriate ratios, where the number of mutual funds is smaller than the number of individual assets in the portfolio. Here a mutual fund refers to any specified benchmark portfolio of the available assets. There are two advantages of having a mutual fund theorem. First, if the relevant conditions are met, it may be easier (or lower in transactions costs) for an investor to purchase a smaller number of mutual funds than to purchase a larger number of assets individually. Second, from a theoretical and empirical standpoint, if it can be assumed that the relevant conditions are indeed satisfied, then implications
Capital asset pricing model
In finance, the capital asset pricing model is used to determine a theoretically appropriate required rate of return of an asset, if that asset is to be added to an already well-diversified portfolio, given that asset's non-diversifiable risk...
for the functioning of asset markets can be derived and tested.
Portfolio separation in mean-variance analysis
Portfolios can be analyzed in a mean-variance framework, with every investor holding the portfolio with the lowest possible return varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
consistent with that investor's chosen level of expected return
Expected return
The expected return is the weighted-average outcome in gambling, probability theory, economics or finance.It isthe average of a probability distribution of possible returns, calculated by using the following formula:...
(called a mean-variance efficient portfolio), if the returns on the assets are jointly elliptically distributed
Elliptical distribution
In probability and statistics, an elliptical distribution is any member of a broad family of probability distributions that generalize the multivariate normal distribution and inherit some of its properties.-Definition:...
, including the special case in which they are jointly normally distributed. Under mean-variance analysis, it can be shown that every variance-minimizing portfolio given a particular expected return (that is, every efficient portfolio) can be formed as a combination of any two efficient portfolios. If the investor's optimal portfolio has an expected return that is between the expected returns on two efficient benchmark portfolios, then that investor's portfolio can be characterized as consisting of positive quantities of the two benchmark portfolios.
No risk-free asset
To see two-fund separation in a context in which no risk-free asset is available, using matrix algebraMatrix algebra
Matrix algebra may refer to:*Matrix theory, is the branch of mathematics that studies matrices*Matrix ring, thought of as an algebra over a field or a commutative ring...
, let
be the variance of the portfolio return, let be the level of expected return on the portfolio that portfolio return variance is to be minimized contingent upon, let be the vector of expected returns on the available assets, let be the vector of amounts to be placed in the available assets, let be the amount of wealth that is to be allocated in the portfolio, and let 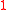be a vector of ones. Then the problem of minimizing the portfolio return variance subject to a given level of expected portfolio return can be stated as- Minimize
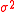
- subject to
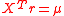
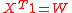
where the superscript
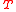denotes the transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of a matrix. The portfolio return variance in the objective function can be written as
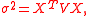where 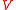is the positive definite covariance matrixCovariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of the individual assets' returns. The Lagrangian
Lagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
for this constrained optimization problem (whose second-order conditions can be shown to be satisfied) is
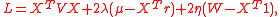
with Lagrange multipliers
and .This can be solved for the optimal vector of asset quantities by equating to zero the derivativesMatrix calculus
In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices, where it defines the matrix derivative. This notation was to describe systems of differential equations, and taking derivatives of matrix-valued functions with respect...
with respect to
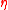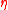, , and , provisionally solving the first-order condition for in terms of and , substituting into the other first-order conditions, solving for and 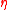in terms of the model parameters, and substituting back into the provisional solution for . The result is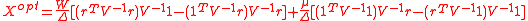where
For simplicity this can be written more compactly as
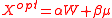
where
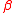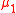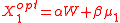
and are parameter vectors based on the underlying model parameters. Now consider two benchmark efficient portfolios constructed at benchmark expected returns and and thus given byand
The optimal portfolio at arbitrary
can then be written as a weighted average of 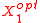and as follows:This equation proves the two-fund separation theorem for mean-variance analysis. For a geometric interpretation, see the Markowitz bullet.
One risk-free asset
If a risk-free assetRisk-free interest rate
Risk-free interest rate is the theoretical rate of return of an investment with no risk of financial loss. The risk-free rate represents the interest that an investor would expect from an absolutely risk-free investment over a given period of time....
is available, then again a two-fund separation theorem applies; but in this case one of the "funds" can be chosen to be a very simple fund containing only the risk-free asset, and the other fund can be chosen to be one which contains zero holdings of the risk-free asset. (With the risk-free asset referred to as "money", this form of the theorem is referred to as the monetary separation theorem.) Thus mean-variance efficient portfolios can be formed simply as a combination of holdings of the risk-free asset and holdings of a particular efficient fund that contains only risky assets. The derivation above does not apply, however, since with a risk-free asset the above covariance matrix of all asset returns,
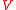, would have one row and one column of zeroes and thus would not be invertible. Instead, the problem can be set up as- Minimize
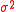
- subject to
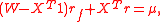
where
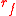is the known return on the risk-free asset, X is now the vector of quantities to be held in the risky assets, and is the vector of expected returns on the risky assets. The left side of the last equation is the expected return on the portfolio, since is the quantity held in the risk-free asset, thus incorporating the asset adding-up constraint that in the earlier problem required the inclusion of a separate Lagrangian constraint. The objective function can be written as 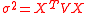, where now 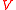is the covariance matrix of the risky assets only. This optimization problem can be shown to yield the optimal vector of risky asset holdings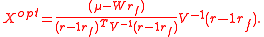Of course this equals a zero vector if
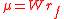, the risk-free portfolio's return, in which case all wealth is held in the risk-free asset. It can be shown that the portfolio with exactly zero holdings of the risk-free asset occurs at 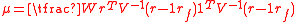and is given by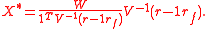It can also be shown (analogously to the demonstration in the above two-mutual-fund case) that every portfolio's risky asset vector (that is,
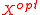for every value of ) can be formed as a weighted combination of the latter vector and the zero vector. For a geometric interpretation, see the efficient frontier with no risk-free asset.Portfolio separation without mean-variance analysis
If investors have hyperbolic absolute risk aversionHyperbolic absolute risk aversion
In finance, economics, and decision theory, hyperbolic absolute risk aversion refers to a type of risk aversion that is particularly convenient to model mathematically and to obtain empirical predictions from...
(HARA) (such as is true for the power utility function and the exponential utility function
Exponential utility
In economics exponential discounting is a specific form of the discount function, used in the analysis of choice over time...
) , separation theorems can be obtained without the use of mean-variance analysis. For example, David Cass
David Cass
David Cass was a professor of economics at the University of Pennsylvania, mostly known for his contributions to general equilibrium theory. His most famous work was on the Ramsey growth model, which is also known as the Ramsey-Cass-Koopmans model.-Biography:David Cass was born in 1937 in...
and Joseph Stiglitz showed in 1970 that two-fund monetary separation applies if all investors have HARA utility with the same exponent as each other.
More recently, in the dynamic portfolio optimization model of Çanakoğlu and Özekici, the investor's level of initial wealth (the distinguishing feature of investors) does not affect the optimal composition of the risky part of the portfolio. A similar result is given by Schmedders.