
Multivariate Student distribution
Encyclopedia
In statistics
, a multivariate Student distribution is a multivariate generalization of the Student's t-distribution. One common method of construction, for the case of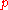 dimensions, is based on the observation that if
dimensions, is based on the observation that if 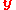 and
and  are independent and distributed as
are independent and distributed as 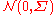 and
and 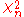 (i.e. multivariate normal and Chi-squared distributions) respectively, then
(i.e. multivariate normal and Chi-squared distributions) respectively, then  is a p x p matrix, and
is a p x p matrix, and 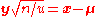 , then
, then  has the density
has the density
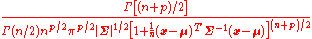
and is said to be distributed as a Multivariate t-distribution with parameters .
.
There are in fact many candidates for the multivariate generalization of Student's t-distribution. An extensive survey of the field has been given by Kotz and Nadarajah (2004). The essential issue is to define a probability density function of several variables that is the appropriate generalization of the formula for the univariate case. In one dimension ( ), with
), with  and
and  , we have the probability density function
, we have the probability density function
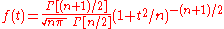
and one approach is to write down a corresponding function of several variables. This is the basic idea of elliptical distribution
theory, where one writes down a corresponding function of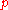 variables
variables 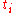 that replaces
that replaces 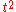 by a quadratic function of all the
by a quadratic function of all the  . It is clear that this only makes sense when all the marginal distributions have the same degrees of freedom
. It is clear that this only makes sense when all the marginal distributions have the same degrees of freedom
 . With
. With  , one has a simple choice of multivariate density function
, one has a simple choice of multivariate density function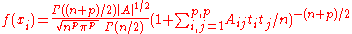
which is the standard but not the only choice.
An important special case is the standard bivariate Student distribution, p = 2:

and if is the identity matrix we have
is the identity matrix we have

The difficulty with the standard representation is revealed by this formula, which does not factorize into the product of the marginal one-dimensional distributions. When is diagonal the standard representation can be shown to have zero correlation
is diagonal the standard representation can be shown to have zero correlation
but the marginal distribution
s are not statistically independent
. There are differing views on this issue, which is under discussion in the research literature as of early 2007.
, especially through the use of the Student t copula
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a multivariate Student distribution is a multivariate generalization of the Student's t-distribution. One common method of construction, for the case of
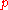 dimensions, is based on the observation that if
dimensions, is based on the observation that if 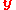 and
and  are independent and distributed as
are independent and distributed as 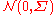 and
and 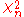 (i.e. multivariate normal and Chi-squared distributions) respectively, then
(i.e. multivariate normal and Chi-squared distributions) respectively, then  is a p x p matrix, and
is a p x p matrix, and 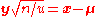 , then
, then  has the density
has the density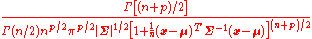
and is said to be distributed as a Multivariate t-distribution with parameters
 .
.There are in fact many candidates for the multivariate generalization of Student's t-distribution. An extensive survey of the field has been given by Kotz and Nadarajah (2004). The essential issue is to define a probability density function of several variables that is the appropriate generalization of the formula for the univariate case. In one dimension (
 ), with
), with  and
and  , we have the probability density function
, we have the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
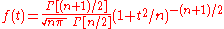
and one approach is to write down a corresponding function of several variables. This is the basic idea of elliptical distribution
Elliptical distribution
In probability and statistics, an elliptical distribution is any member of a broad family of probability distributions that generalize the multivariate normal distribution and inherit some of its properties.-Definition:...
theory, where one writes down a corresponding function of
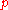 variables
variables 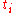 that replaces
that replaces 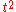 by a quadratic function of all the
by a quadratic function of all the  . It is clear that this only makes sense when all the marginal distributions have the same degrees of freedom
. It is clear that this only makes sense when all the marginal distributions have the same degrees of freedomDegrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
 . With
. With  , one has a simple choice of multivariate density function
, one has a simple choice of multivariate density function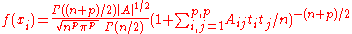
which is the standard but not the only choice.
An important special case is the standard bivariate Student distribution, p = 2:

and if
 is the identity matrix we have
is the identity matrix we have
The difficulty with the standard representation is revealed by this formula, which does not factorize into the product of the marginal one-dimensional distributions. When
 is diagonal the standard representation can be shown to have zero correlation
is diagonal the standard representation can be shown to have zero correlationPearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
but the marginal distribution
Marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
s are not statistically independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
. There are differing views on this issue, which is under discussion in the research literature as of early 2007.
Further theory
Many such distributions may be constructed by considering the quotients of normal random variables with the square root of a sample from a chi-squared distribution. These are surveyed in the references and links below.Copulas based on the multivariate Student
The use of such distributions is enjoying renewed interest due to applications in mathematical financeMathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
, especially through the use of the Student t copula
Copula (statistics)
In probability theory and statistics, a copula can be used to describe the dependence between random variables. Copulas derive their name from linguistics....
.
See also
- Student's t-testStudent's t-testA t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known...
in univariate statistics - Student's t-distribution in univariate probability theory
- Hotelling's T-squared distribution in multivariate statistics

