
Multiobjective optimization
Encyclopedia
Multi-objective optimization (or multi-objective programming), also known as multi-criteria or multi-attribute optimization, is the process of simultaneously optimizing two or more conflicting objectives subject to certain constraints.
Multiobjective optimization problems can be found in various fields: product and process design, finance, aircraft design, the oil and gas industry, automobile design, or wherever optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Maximizing profit and minimizing the cost of a product; maximizing performance and minimizing fuel consumption of a vehicle; and minimizing weight while maximizing the strength of a particular component are examples of multi-objective optimization problems.
For nontrivial multiobjective problems, one cannot identify a single solution that simultaneously optimizes each objective. While searching for solutions, one reaches points such that, when attempting to improve an objective further, other objectives suffer as a result.
A tentative solution is called non-dominated, Pareto optimal, or Pareto efficient if it cannot be eliminated from consideration by replacing it with another solution which improves an objective without worsening another one.
Finding such non-dominated solutions, and quantifying the trade-offs in satifying the different objectives, is the goal when setting up and solving a multiobjective optimization problem.
Multiobjective optimization problems can be found in various fields: product and process design, finance, aircraft design, the oil and gas industry, automobile design, or wherever optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Maximizing profit and minimizing the cost of a product; maximizing performance and minimizing fuel consumption of a vehicle; and minimizing weight while maximizing the strength of a particular component are examples of multi-objective optimization problems.
For nontrivial multiobjective problems, one cannot identify a single solution that simultaneously optimizes each objective. While searching for solutions, one reaches points such that, when attempting to improve an objective further, other objectives suffer as a result.
A tentative solution is called non-dominated, Pareto optimal, or Pareto efficient if it cannot be eliminated from consideration by replacing it with another solution which improves an objective without worsening another one.
Finding such non-dominated solutions, and quantifying the trade-offs in satifying the different objectives, is the goal when setting up and solving a multiobjective optimization problem.
Introduction
In mathematical terms, the multiobjective problem can be written as:-
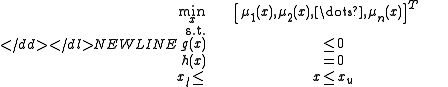
where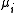 is the
is the 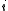 -th objective function,
-th objective function, 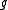 and
and 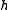 are the inequality and equality constraints, respectively, and
are the inequality and equality constraints, respectively, and  is the vector of optimization or decision variables. The solution to the above problem is a set of Pareto points. Thus, instead of being a unique solution to the problem, the solution to a multiobjective problem is a possibly infinite set of Pareto points.
is the vector of optimization or decision variables. The solution to the above problem is a set of Pareto points. Thus, instead of being a unique solution to the problem, the solution to a multiobjective problem is a possibly infinite set of Pareto points.
A design point in objective space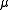 is termed Pareto optimalPareto efficiencyPareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
is termed Pareto optimalPareto efficiencyPareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
if there does not exist another feasible design objective vector such that
such that  for all
for all 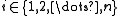 , and
, and 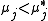 for at least one index of
for at least one index of 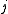 ,
,  .
.
Solution methods
There exist many methods to finding a solution to a multiobjective optimization problem, some of which are explained below:
Constructing a single aggregate objective function (AOF)
This is an intuitive approach to solving the multi-objective problem. The basic idea is to combine all of the objectives into a single objective function, called the AOF, such as the well-known weighted linear sum of the objectives. This objective function is optimized subject to technological constraints specifying how much of one objective must be sacrificed, from any given starting point, in order to gain a certain amount regarding the other objective. These technological constraints frequently come in the form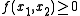 for some function f, where
for some function f, where 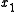 and
and 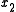 are the objectives (e.g., strength and lightness of a product).
are the objectives (e.g., strength and lightness of a product).
Often the aggregate objective function is not linear in the objectives, but rather is non-linear, expressing increasing marginal dissatisfaction with greater incremental sacrifices in the value of either objective. Furthermore, sometimes the aggregate objective function is additively separable, so that it is expressed as a weighted average of a non-linear function of one objective and a non-linear function of another objective. Then the optimal solution obtained will depend on the relative values of the weights specified. For example, if one is trying to maximize the strength of a machine component and minimize the production cost, and if a higher weight is specified for the cost objective compared to the strength, the solution will be one that favors lower cost over higher strength.
The weighted sum method, like any method of selecting a single solution as preferable to all others, is essentially subjective, in that a decision manager needs to supply the weights. Moreover, this approach may prove difficult to implement if the Pareto frontier is not globally convex and/or the objective function to be minimized is not globally concave.
The objective way of characterizing multi-objective problems, by identifying multiple Pareto optimal candidate solutions, requires a Pareto-compliant ranking method, favoring non-dominated solutions, as seen in current multi-objective evolutionary approaches such as NSGA-II and SPEA2. Here, no weight is required and thus no a priori information on the decision-maker's preferences is needed. However, to decide upon one of the Pareto-efficient options as the one to adopt requires information about the decision-maker's preferences. Thus the objective characterization of the problem is simply the first stage in a two-stage analysis, consisting of (1) identifying the non-dominated possibilities, and (2) choosing among them.
The NBI, NC, SPO and DSD methods
The Normal Boundary Intersection (NBI), Normal Constraint (NC), Successive Pareto Optimization (SPO), and Directed Search Domain (DSD) methods solve the multi-objective optimization problem by constructing several AOFs. The solution of each AOF yields a Pareto point, whether locally or globally.
The NC and DSD methods suggest two different filtering procedures to remove locally Pareto points. The AOFs are constructed with the target of obtaining evenly distributed Pareto points that give a good impression (approximation) of the real set of Pareto points.
The DSD, NC and SPO methods generate solutions that represent some peripheral regions of the set of Pareto points for more than two objectives that are known to be not represented by the solutions generated with the NBI method.
According to Erfani and Utyuzhnikov, the DSD method works reasonably more efficiently than its NC and NBI counterparts on some difficult test cases in the literature.
Evolutionary algorithms
Evolutionary algorithms are popular approaches to solving multiobjective optimization. Currently most evolutionary optimizers apply Pareto-based ranking schemes. Genetic algorithms such as the Non-dominated Sorting Genetic Algorithm-II (NSGA-II) and Strength Pareto Evolutionary Algorithm 2 (SPEA-2) have become standard approaches, although some schemes based on particle swarm optimization and simulated annealingSimulated annealingSimulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
are significant. The main advantage of evolutionary algorithms, when applied to solve multi-objective optimization problems, is the fact that they typically optimize sets of solutions, allowing computation of an approximation of the entire Pareto front in a single algorithm run. The main disadvantage of evolutionary algorithms is the much lower speed.
Other methods
- Multiobjective Optimization using Evolutionary Algorithms (MOEA).
- PGEN (Pareto surface generation for convex multiobjective instances)
- IOSOIOSOIOSO is a multiobjective, multidimensional nonlinear optimization technology.-IOSO approach:IOSO Technology is based on the response surface methodology approach....
(Indirect Optimization on the basis of Self-Organization)
Economics
In economicsEconomicsEconomics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, the study of resource allocation under scarcity, many problems involve multiple objectives along with constraints on what combinations of those objectives are attainable.
For example, a consumer's demandDemand- Economics :*Demand , the desire to own something and the ability to pay for it*Demand curve, a graphic representation of a demand schedule*Demand deposit, the money in checking accounts...
s for various goods are determined by the process of maximization of the utilityUtilityIn economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
derived from those goods, subject to a constraint based on how much income is available to spend on those goods and on the prices of those goods. This constraint allows more of one good to be purchased only at the sacrifice of consuming less of another good; therefore, the various objectives (more consumption of each good is preferred) are in conflict with each other according to this constraint. A common method for analyzing such a problem is to use a graph of indifference curveIndifference curveIn microeconomic theory, an indifference curve is a graph showing different bundles of goods between which a consumer is indifferent. That is, at each point on the curve, the consumer has no preference for one bundle over another. One can equivalently refer to each point on the indifference curve...
s, representing preferences, and a budget constraint, representing the trade-offs that the consumer is faced with.
Another example involves the production possibilities frontier, which specifies what combinations of various types of goods can be produced by a society with certain amounts of various resources. The frontier specifies the trade-offs that the society is faced with — if the society is fully utilizing its resources, more of one good can be produced only at the expense of producing less of another good. A society must then use some process to choose among the possibilities on the frontier.
Macroeconomic policy-making is a context requiring multi-objective optimization. Typically a central bankCentral bankA central bank, reserve bank, or monetary authority is a public institution that usually issues the currency, regulates the money supply, and controls the interest rates in a country. Central banks often also oversee the commercial banking system of their respective countries...
must choose a stance for monetary policyMonetary policyMonetary policy is the process by which the monetary authority of a country controls the supply of money, often targeting a rate of interest for the purpose of promoting economic growth and stability. The official goals usually include relatively stable prices and low unemployment...
that balances competing objectives — low inflationInflationIn economics, inflation is a rise in the general level of prices of goods and services in an economy over a period of time.When the general price level rises, each unit of currency buys fewer goods and services. Consequently, inflation also reflects an erosion in the purchasing power of money – a...
, low unemploymentUnemploymentUnemployment , as defined by the International Labour Organization, occurs when people are without jobs and they have actively sought work within the past four weeks...
, low balance of tradeBalance of tradeThe balance of trade is the difference between the monetary value of exports and imports of output in an economy over a certain period. It is the relationship between a nation's imports and exports...
deficit, etc. To do this, the central bank uses a model of the economy that quantitatively describes the various causal linkages in the economy; it simulatesSimulationSimulation is the imitation of some real thing available, state of affairs, or process. The act of simulating something generally entails representing certain key characteristics or behaviours of a selected physical or abstract system....
the model repeatedly under various possible stances of monetary policy, in order to obtain a menu of possible predicted outcomes for the various variables of interest. Then in principle it can use an aggregate objective function to rate the alternative sets of predicted outcomes, although in practice central banks use a non-quantitative, judgement-based, process for ranking the alternatives and making the policy choice.
Finance
In financeFinance"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, a common problem is to choose a portfolio when there are two conflicting objectives — the desire to have the expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of portfolio returns be as high as possible, and the desire to have riskFinancial riskFinancial risk an umbrella term for multiple types of risk associated with financing, including financial transactions that include company loans in risk of default. Risk is a term often used to imply downside risk, meaning the uncertainty of a return and the potential for financial loss...
, measured by the standard deviationStandard deviationStandard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of portfolio returns, be as low as possible. This problem is often represented by a graph in which the efficient frontierEfficient FrontierThe efficient frontier is a concept in Modern portfolio theory introduced by Harry Markowitz and others. A combination of assets, i.e. a portfolio, is referred to as "efficient" if it has the best possible expected level of return for its level of risk...
shows the best combinations of risk and expected return that are available, and in which indifference curves show the investor's preferences for various risk-expected return combinations. The problem of optimizing a function of the expected value (first momentMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
) and the standard deviation (square root of the second moment) of portfolio return is called a two-moment decision model.
Linear programming applications
In linear programming problems, a linear objective function is optimized subject to linear constraints. Typically multiple variables of concern appear in the objective function. A vast body of research has been devoted to methods of solving these problems. Because the efficient set, the set of combinations of values of the various variables of interest having the feature that none of the variables can be given a better value without hurting the value of another variable, is piecewise linearPiecewise linear manifoldIn mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...
and not continuously differentiable, the problem is not dealt with by first specifying all the points on the Pareto-efficient set; instead, solution procedures utilize the aggregate objective function right from the start.
Many practical problems in operations researchOperations researchOperations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
can be expressed as linear programming problems. Certain special cases of linear programming, such as network flow problems and multi-commodity flow problemMulti-commodity flow problemThe multi-commodity flow problem is a network flow problem with multiple commodities flowing through the network, with different source and sink nodes.-Definition:Given a flow network \,G, where edge \in E has capacity \,c...
s are considered important enough to have generated much research on specialized algorithms for their solution. Linear programming is heavily used in microeconomicsMicroeconomicsMicroeconomics is a branch of economics that studies the behavior of how the individual modern household and firms make decisions to allocate limited resources. Typically, it applies to markets where goods or services are being bought and sold...
and company managementManagementManagement in all business and organizational activities is the act of getting people together to accomplish desired goals and objectives using available resources efficiently and effectively...
, for dealing with such issues as planning, production, transportation, technology, and so forth.
Optimal control applications
In engineeringEngineeringEngineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
and economicsEconomicsEconomics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, many problems involve multiple objectives which are not describable as the-more-the-better or the-less-the-better; instead, there is an ideal target value for each objective, and the desire is to get as close as possible to the desired value of each objective. For example, one might want to adjust a rocket's fuel usage and orientation so that it arrives both at a specified place and at a specified time; or one might want to conduct open market operations so that both the inflation rateInflation rateIn economics, the inflation rate is a measure of inflation, the rate of increase of a price index . It is the percentage rate of change in price level over time. The rate of decrease in the purchasing power of money is approximately equal.The inflation rate is used to calculate the real interest...
and the unemployment rate are as close as possible to their desired values.
Often such problems are subject to linear equality constraints that prevent all objectives from being simultaneously perfectly met, especially when the number of controllable variables is less than the number of objectives and when the presence of random shocks generates uncertainty. Commonly a multi-objective quadratic objective function is used, with the cost associated with an objective rising quadratically with the distance of the objective from its ideal value. Since these problems typically involve adjusting the controlled variables at various points in time and/or evaluating the objectives at various points in time, intertemporal optimization techniques are employed.
See also
- Multidisciplinary design optimizationMultidisciplinary design optimizationMulti-disciplinary design optimization is a field of engineering that uses optimization methods to solve design problems incorporating a number of disciplines. As defined by Prof. Carlo Poloni, MDO is "the art of finding the best compromise"...
- Pareto efficiencyPareto efficiencyPareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
- Goal ProgrammingGoal programmingGoal programming is a branch of multiobjective optimization, which in turn is a branch of multi-criteria decision analysis , also known as multiple-criteria decision making . This is an optimization programme. It can be thought of as an extension or generalisation of linear programming to handle...
- PolytelyPolytelyPolytely can be described as frequently, complex problem-solving situations characterized by the presence of not one, but several goals, endings.Modern societies face an increasing incidence of various complex problems...
- Concurrent programming
- Multi-criteria decision analysisMulti-Criteria Decision AnalysisMultiple-criteria decision-making or multiple-criteria decision analysis is a sub-discipline of operations research that explicitly considers multiple criteria in decision-making environments. Whether in our daily lives or in professional settings, there are typically multiple conflicting criteria...
External links
- A tutorial on multiobjective optimization
- Evolutionary Multiobjective Optimization, The Wolfram Demonstrations Project

