
Multinomial logit
Encyclopedia
In statistics
, economics
, and genetics
, a multinomial logit
(MNL) model, also known as multinomial logistic regression, is a regression
model which generalizes logistic regression
by allowing more than two discrete outcomes. That is, it is a model that is used to predict the probabilities of the different possible outcomes of a categorically distributed
dependent variable, given a set of independent variable
s (which may be real-valued, binary-valued, categorical-valued, etc.).
In some fields of machine learning
(e.g. natural language processing
), when a classifier is implemented using a multinomial logit model, it is commonly known as a maximum entropy classifier, or MaxEnt model for short. Maximum entropy classifiers are commonly used as alternatives to Naive Bayes classifier
s because they do not assume statistical independence
of the independent variables (commonly known as features) that serve as predictors. However, learning in such a model is significantly slower than for a Naive Bayes classifier, and thus may not be appropriate given a very large number of classes to learn. In particular, learning in a Naive Bayes classifier is a simple matter of counting up the number of cooccurrences of features and classes, while in a maximum entropy classifier the weights, which are typically maximized using maximum a posteriori
(MAP) estimation, must be learned using an iterative procedure; see below.
Multinomial logit regression is appropriate in cases where the response is not ordinal in nature as in ordered logit
. Ordered logit regression is used in cases where the dependent variable in question consists of a set number (more than two) of categories which can be ordered in a meaningful way (for example, highest degree, social class) while multinomial logit is used when there is no apparent order (e.g. the choice of muffins, bagels or doughnuts for breakfast) .
); however, collinearity
is assumed to be relatively low, as it becomes difficult to differentiate between the impact of several variables if they are highly correlated.
If the multinomial logit is used to model choices, it relies on the assumption of independence of irrelevant alternatives
(IIA) which is not always desirable. This assumption states that the odds do not depend on other alternatives that are not relevant (e.g. the relative probabilities of taking a car or bus to work do not change if a bicycle is added as an additional possibility). The IIA hypothesis is a core hypothesis in rational choice theory; however numerous studies in psychology show that individuals often violate this assumption when making choices. An example of a problem case arises if choices include a car and a blue bus. Suppose the odds ratio between the two is 1 : 1. Now if the option of a red bus is introduced, a person may be indifferent between a red and a blue bus, and hence may exhibit a car : blue bus : red bus odds ratio of 1 : 0.5 : 0.5, thus maintaining a 1 : 1 ratio of car : any bus while adopting a changed car : blue bus ratio of 1 : 0.5. Here the red bus option was not in fact irrelevant, because a red bus was a perfect substitute for a blue bus.
If the multinomial logit is used to model choices, it may in some situations impose too much constraint on the relative preferences between the different alternatives. This point is especially important to take into account if the analysis aims to predict how choices would change if one alternative was to disappear (for instance if one political candidate withdraws from a three candidate race). Other models like the nested logit or the multinomial probit
may be used in such cases as they need not violate the IIA.
s are determined for all independent variables for each category of the dependent variable with the exception of the reference category, which is omitted from the analysis. The exponential beta coefficient represents the change in the odds of the dependent variable being in a particular category vis-a-vis the reference category, associated with a one unit change of the corresponding independent variable.
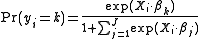
and to ensure satisfaction of the adding-up constraint,
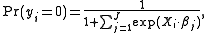
where yi is the observed outcome for the ith observation on the dependent variable, Xi is a vector
of the ith observations of all the explanatory variables, and β j is a vector of all the regression coefficients in the jth regression. The unknown parameters in each vector βj are typically jointly estimated by maximum a posteriori
(MAP) estimation, which is an extension of maximum likelihood
using regularization
of the weights to prevent pathological solutions (usually a squared regularizing function, which is equivalent to placing a zero-mean Gaussian prior distribution on the weights, but other distributions are also possible). The solution is typically found using an iterative procedure such as iteratively reweighted least squares (IRLS) or, more commonly these days, a quasi-Newton method
such as the L-BFGS method
.
models combine a random ensemble of multinomial logit models for use as a classifier.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, and genetics
Genetics
Genetics , a discipline of biology, is the science of genes, heredity, and variation in living organisms....
, a multinomial logit
Logistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
(MNL) model, also known as multinomial logistic regression, is a regression
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
model which generalizes logistic regression
Logistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
by allowing more than two discrete outcomes. That is, it is a model that is used to predict the probabilities of the different possible outcomes of a categorically distributed
Categorical distribution
In probability theory and statistics, a categorical distribution is a probability distribution that describes the result of a random event that can take on one of K possible outcomes, with the probability of each outcome separately specified...
dependent variable, given a set of independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s (which may be real-valued, binary-valued, categorical-valued, etc.).
In some fields of machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
(e.g. natural language processing
Natural language processing
Natural language processing is a field of computer science and linguistics concerned with the interactions between computers and human languages; it began as a branch of artificial intelligence....
), when a classifier is implemented using a multinomial logit model, it is commonly known as a maximum entropy classifier, or MaxEnt model for short. Maximum entropy classifiers are commonly used as alternatives to Naive Bayes classifier
Naive Bayes classifier
A naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem with strong independence assumptions...
s because they do not assume statistical independence
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of the independent variables (commonly known as features) that serve as predictors. However, learning in such a model is significantly slower than for a Naive Bayes classifier, and thus may not be appropriate given a very large number of classes to learn. In particular, learning in a Naive Bayes classifier is a simple matter of counting up the number of cooccurrences of features and classes, while in a maximum entropy classifier the weights, which are typically maximized using maximum a posteriori
Maximum a posteriori
In Bayesian statistics, a maximum a posteriori probability estimate is a mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data...
(MAP) estimation, must be learned using an iterative procedure; see below.
Introduction
Multinomial logit regression is used when the dependent variable in question is nominal (a set of categories which cannot be ordered in any meaningful way, also known as categorical) and consists of more than two categories. For example, multinomial logit regression would be appropriate when trying to determine what factors predict which major college students choose.Multinomial logit regression is appropriate in cases where the response is not ordinal in nature as in ordered logit
Ordered logit
In statistics, the ordered logit model , is a regression model for ordinal dependent variables...
. Ordered logit regression is used in cases where the dependent variable in question consists of a set number (more than two) of categories which can be ordered in a meaningful way (for example, highest degree, social class) while multinomial logit is used when there is no apparent order (e.g. the choice of muffins, bagels or doughnuts for breakfast) .
Assumptions
The multinomial logit model assumes that data are case specific; that is, each independent variable has a single value for each case. The multinomial logit model also assumes that the dependent variable cannot be perfectly predicted from the independent variables for any case. As with other types of regression, there is no need for the independent variables to be statistically independent from each other (unlike, for example, in a Naive Bayes classifierNaive Bayes classifier
A naive Bayes classifier is a simple probabilistic classifier based on applying Bayes' theorem with strong independence assumptions...
); however, collinearity
Multicollinearity
Multicollinearity is a statistical phenomenon in which two or more predictor variables in a multiple regression model are highly correlated. In this situation the coefficient estimates may change erratically in response to small changes in the model or the data...
is assumed to be relatively low, as it becomes difficult to differentiate between the impact of several variables if they are highly correlated.
If the multinomial logit is used to model choices, it relies on the assumption of independence of irrelevant alternatives
Independence of irrelevant alternatives
Independence of irrelevant alternatives is an axiom of decision theory and various social sciences.The word is used in different meanings in different contexts....
(IIA) which is not always desirable. This assumption states that the odds do not depend on other alternatives that are not relevant (e.g. the relative probabilities of taking a car or bus to work do not change if a bicycle is added as an additional possibility). The IIA hypothesis is a core hypothesis in rational choice theory; however numerous studies in psychology show that individuals often violate this assumption when making choices. An example of a problem case arises if choices include a car and a blue bus. Suppose the odds ratio between the two is 1 : 1. Now if the option of a red bus is introduced, a person may be indifferent between a red and a blue bus, and hence may exhibit a car : blue bus : red bus odds ratio of 1 : 0.5 : 0.5, thus maintaining a 1 : 1 ratio of car : any bus while adopting a changed car : blue bus ratio of 1 : 0.5. Here the red bus option was not in fact irrelevant, because a red bus was a perfect substitute for a blue bus.
If the multinomial logit is used to model choices, it may in some situations impose too much constraint on the relative preferences between the different alternatives. This point is especially important to take into account if the analysis aims to predict how choices would change if one alternative was to disappear (for instance if one political candidate withdraws from a three candidate race). Other models like the nested logit or the multinomial probit
Multinomial probit
In econometrics and statistics, the multinomial probit model, a popular alternative to the multinomial logit model, is a generalization of the probit model that allows more than two discrete, unordered outcomes. It is not to be confused with the multivariate probit model, which is used to model...
may be used in such cases as they need not violate the IIA.
Estimation of intercept
When using multinomial logistic regression, one category of the dependent variable is chosen as the reference category. Separate odds ratioOdds ratio
The odds ratio is a measure of effect size, describing the strength of association or non-independence between two binary data values. It is used as a descriptive statistic, and plays an important role in logistic regression...
s are determined for all independent variables for each category of the dependent variable with the exception of the reference category, which is omitted from the analysis. The exponential beta coefficient represents the change in the odds of the dependent variable being in a particular category vis-a-vis the reference category, associated with a one unit change of the corresponding independent variable.
Model
Let there be dependent variable categories 0, 1, ..., J with 0 being the reference category. One regression is run for each category 1, 2, ..., J to predict the probability of yi ( the dependent variable for any observation i) being in that category. Then the probability of yi being in category 0 is given by the adding-up constraint that the sum of the probabilities of yi being in the various categories equals one. The regressions are, for k = 1, 2, ..., J: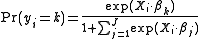
and to ensure satisfaction of the adding-up constraint,
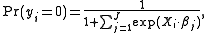
where yi is the observed outcome for the ith observation on the dependent variable, Xi is a vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of the ith observations of all the explanatory variables, and β j is a vector of all the regression coefficients in the jth regression. The unknown parameters in each vector βj are typically jointly estimated by maximum a posteriori
Maximum a posteriori
In Bayesian statistics, a maximum a posteriori probability estimate is a mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data...
(MAP) estimation, which is an extension of maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
using regularization
Regularization (mathematics)
In mathematics and statistics, particularly in the fields of machine learning and inverse problems, regularization involves introducing additional information in order to solve an ill-posed problem or to prevent overfitting...
of the weights to prevent pathological solutions (usually a squared regularizing function, which is equivalent to placing a zero-mean Gaussian prior distribution on the weights, but other distributions are also possible). The solution is typically found using an iterative procedure such as iteratively reweighted least squares (IRLS) or, more commonly these days, a quasi-Newton method
Quasi-Newton method
In optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
such as the L-BFGS method
L-BFGS
The limited-memory BFGS algorithm is a member of the broad family of quasi-Newton optimization methods that uses a limited memory variation of the Broyden–Fletcher–Goldfarb–Shanno update to approximate the inverse Hessian matrix...
.
Applications
Random multinomial logitRandom multinomial logit
In statistics and machine learning, random multinomial logit is a technique for statistical classification using repeated multinomial logit analyses via Leo Breiman's random forests.-Rationale for the new method:...
models combine a random ensemble of multinomial logit models for use as a classifier.

