Mooney-Rivlin solid
Encyclopedia
In continuum mechanics
, a Mooney–Rivlin solid is a hyperelastic material
model where the strain energy density function
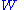is a linear combination of two invariants
of the left Cauchy–Green deformation tensor
. The model was proposed by Melvin Mooney
in 1940 and expressed in terms of invariants by Ronald Rivlin
in 1948.
The strain energy density function for an incompressible Mooney–Rivlin material is
where
and 
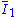are empirically determined material constants, and 
and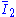 
are the first and the second invariant
of the unimodular
component of the left Cauchy–Green deformation tensor:
where
is the deformation gradient. For an incompressible material, 
.
) which has the form
with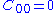
where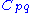 
are material constants related to the distortional response and 
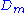are material constants related to the volumetric response. For a compressible Mooney–Rivlin material 
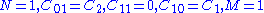and we have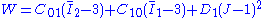
If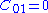
we obtain a neo-Hookean solid
, a special case of a Mooney–Rivlin solid.
For consistency with linear elasticity
in the limit of small strains, it is necessary that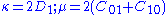
where
is the bulk modulus
and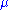
is the shear modulus.
in a compressible hyperelastic material with a stress free reference configuration is given by
For a compressible Mooney–Rivlin material,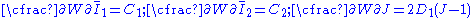
Therefore, the Cauchy stress in a compressible Mooney–Rivlin material is given by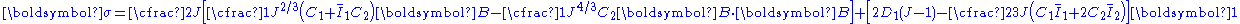
The quantity
has the form of a pressure
. The stress can then be expressed in the form
For an incompressible Mooney–Rivlin material with
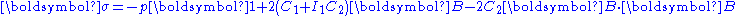
Note that if
then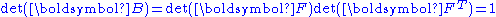
Then, from the Cayley-Hamilton theorem,
Hence, the Cauchy stress can be expressed as
where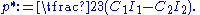
For an incompressible Mooney-Rivlin material,
Therefore,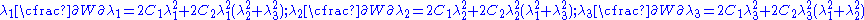
Since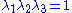
. we can write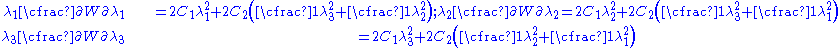
Then the expressions for the Cauchy stress differences become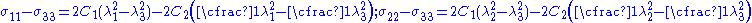
and 
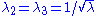. Then the true stress
(Cauchy stress) differences can be calculated as:
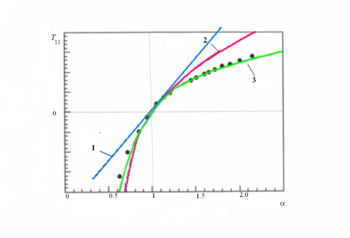In the case of simple tension, 
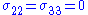. Then we can write
In alternative notation, where the Cauchy stress is written as
and the stretch as 
, we can write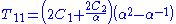
and the engineering stress (force per unit reference area) for an incompressible Mooney–Rivlin material under simple tension can be calculated using
. Hence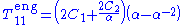
If we define
then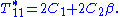
The slope of the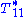
versus 
line gives the value of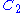 
while the intercept with the 
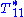axis gives the value of 
. The Mooney–Rivlin solid model usually fits experimental data better than Neo-Hookean solid
does, but requires an additional empirical constant.
. If, in addition, the material is incompressible then 
. The Cauchy stress differences may therefore be expressed as
The equations for equibiaxial tension are equivalent to those governing uniaxial compression.
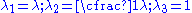
The Cauchy stress differences for pure shear may therefore be expressed as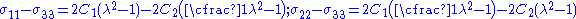
Therefore
For a pure shear deformation
Therefore
.
where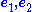
are reference orthonormal basis vectors in the plane of deformation and the shear deformation is given by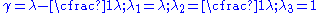
In matrix form, the deformation gradient and the left Cauchy-Green deformation tensor may then be expressed as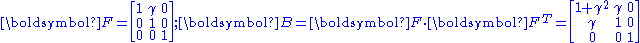
Therefore,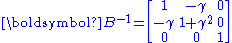
The Cauchy stress is given by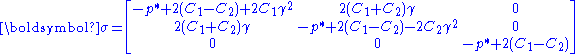
For consistency with linear elasticity, clearly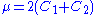
where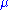 
is the shear modulus.
are determined by the fitting predicted stress from the above equations to experimental data. The recommended tests are uniaxial tension, equibiaxial compression, equibiaxial tension, uniaxial compression, and for shear, planar tension and planar compression. The two parameter Mooney–Rivlin model is usually valid for strains less than 100%.
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, a Mooney–Rivlin solid is a hyperelastic material
Hyperelastic material
A hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
model where the strain energy density function
Strain energy density function
A strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
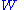is a linear combination of two invariantsInvariants of tensors
In mathematics, in the fields of multilinear algebra and representation theory, invariants of tensors are coefficients of the characteristic polynomial of the tensor A:\ p:=\det ,...
of the left Cauchy–Green deformation tensor
. The model was proposed by Melvin MooneyMelvin Mooney
Melvin Mooney was an American physicist and rheologist.He developed the Mooney Viscometer and other testing equipment used in the rubber industry. He also proposed the Mooney-Rivlin solid constitutive law describing the hyperelastic stress-strain behavior of rubber...
in 1940 and expressed in terms of invariants by Ronald Rivlin
Ronald Rivlin
Ronald Samuel Rivlin was a British-American physicist, mathematician, rheologist and a noted expert on rubber.-Life:Rivlin was born in London in 1915. He studied physics and mathematics at St John's College, Cambridge, being awarded a BA in 1937 and a ScD in 1952...
in 1948.
The strain energy density function for an incompressible Mooney–Rivlin material is
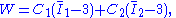
where
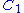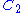and are empirically determined material constants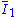, and and 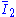are the first and the second invariantInvariants of tensors
In mathematics, in the fields of multilinear algebra and representation theory, invariants of tensors are coefficients of the characteristic polynomial of the tensor A:\ p:=\det ,...
of the unimodular
Unimodular matrix
In mathematics, a unimodular matrix M is a square integer matrix with determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N which is its inverse...
component of the left Cauchy–Green deformation tensor:
where
is the deformation gradient. For an incompressible material, .Derivation
The Mooney–Rivlin model is a special case of the generalized Rivlin model (also called polynomial hyperelastic modelPolynomial (hyperelastic model)
The polynomial hyperelastic material model is a phenomenological model of rubber elasticity. In this model, the strain energy density function is of the form of a polynomial in the two invariants I_1,I_2 of the left Cauchy-Green deformation tensor....
) which has the form
with
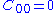where 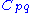are material constants related to the distortional response and 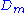are material constants related to the volumetric response. For a compressible Mooney–Rivlin material 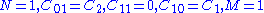and we have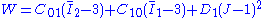If
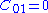we obtain a neo-Hookean solidNeo-Hookean solid
A Neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948. In contrast to linear elastic materials, a the...
, a special case of a Mooney–Rivlin solid.
For consistency with linear elasticity
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
in the limit of small strains, it is necessary that
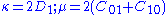
where
is the bulk modulusBulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
and
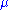is the shear modulus.Cauchy stress in terms of strain invariants and deformation tensors
The Cauchy stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
in a compressible hyperelastic material with a stress free reference configuration is given by
For a compressible Mooney–Rivlin material,
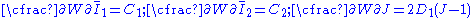
Therefore, the Cauchy stress in a compressible Mooney–Rivlin material is given by
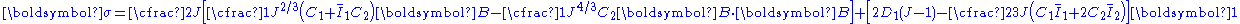
The quantity
has the form of a pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
. The stress can then be expressed in the form
For an incompressible Mooney–Rivlin material with
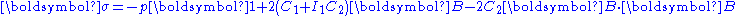
Note that if
then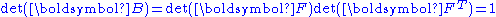Then, from the Cayley-Hamilton theorem,
Hence, the Cauchy stress can be expressed as
where
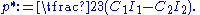
Cauchy stress in terms of principal stretches
In terms of the principal stretches, the Cauchy stress differences for an incompressible hyperelastic material are given byFor an incompressible Mooney-Rivlin material,
Therefore,
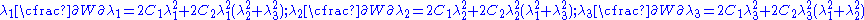
Since
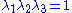. we can write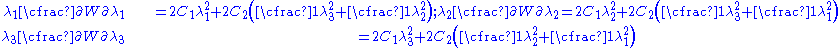Then the expressions for the Cauchy stress differences become
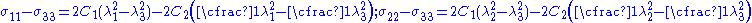
Uniaxial extension
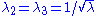For the case of an incompressible Mooney–Rivlin material under uniaxial elongation, and . Then the true stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
(Cauchy stress) differences can be calculated as:
Simple tension
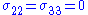. Then we can writeIn alternative notation, where the Cauchy stress is written as
and the stretch as , we can write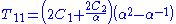and the engineering stress (force per unit reference area) for an incompressible Mooney–Rivlin material under simple tension can be calculated using
. Hence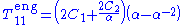If we define
then
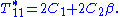
The slope of the
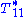versus line gives the value of 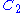while the intercept with the 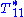axis gives the value of . The Mooney–Rivlin solid model usually fits experimental data better than Neo-Hookean solidNeo-Hookean solid
A Neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948. In contrast to linear elastic materials, a the...
does, but requires an additional empirical constant.
Equibiaxial tension
In the case of equibiaxial tension, the principal stretches are. If, in addition, the material is incompressible then . The Cauchy stress differences may therefore be expressed asThe equations for equibiaxial tension are equivalent to those governing uniaxial compression.
Pure shear
A pure shear deformation can be achieved by applying stretches of the form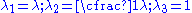The Cauchy stress differences for pure shear may therefore be expressed as
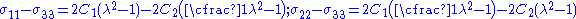
Therefore
For a pure shear deformation
Therefore
.Simple shear
The deformation gradient for a simple shear deformation has the formwhere
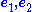are reference orthonormal basis vectors in the plane of deformation and the shear deformation is given by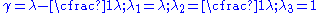In matrix form, the deformation gradient and the left Cauchy-Green deformation tensor may then be expressed as
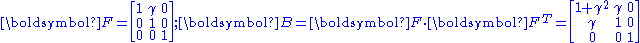
Therefore,
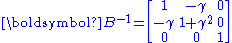
The Cauchy stress is given by
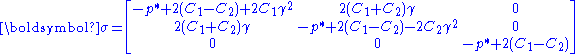
For consistency with linear elasticity, clearly
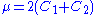where 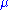is the shear modulus.Rubber
Elastic response of rubber-like materials are often modeled based on the Mooney—Rivlin model. The constants are determined by the fitting predicted stress from the above equations to experimental data. The recommended tests are uniaxial tension, equibiaxial compression, equibiaxial tension, uniaxial compression, and for shear, planar tension and planar compression. The two parameter Mooney–Rivlin model is usually valid for strains less than 100%.See also
- Hyperelastic materialHyperelastic materialA hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
- Finite strain theory
- Continuum mechanicsContinuum mechanicsContinuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
- Strain energy density functionStrain energy density functionA strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....