Miller-Rabin primality test
Encyclopedia
The Miller–Rabin primality test or Rabin–Miller primality test is a primality test
: an algorithm
which determines whether a given number is prime
,
similar to the Fermat primality test
and the Solovay–Strassen primality test. Its original version, due to Gary L. Miller
, is deterministic
, but the determinism relies on the unproven generalized Riemann hypothesis
; Michael O. Rabin
modified it to obtain an unconditional probabilistic algorithm
.
First, a lemma
about square roots of unity
in the finite field
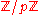, where p is prime and p > 2. Certainly 1 and −1 always yield 1 when squared mod p; call these trivial
square root
s of 1. There are no nontrivial square roots of 1 mod p (a special case of the result that, in a field, a polynomial has no more zeroes than its degree). To show this, suppose that x is a square root of 1 mod p. Then:
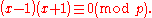
In other words, p divides the product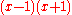
. It thus divides one of the factors and it follows that x is either congruent to 1 or −1 mod p.
Now, let n be an odd prime. Then n−1 is even and we can write it as 2s·d, where s and d are positive integers (d is odd). For each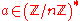
, either
or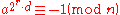
for some 
To show that one of these must be true, recall Fermat's little theorem
:
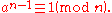
By the lemma above, if we keep taking square roots of an − 1, we will get either 1 or −1. If we get −1 then the second equality holds and we are done. If we never get −1, then when we have taken out every power of 2, we are left with the first equality.
The Miller–Rabin primality test is based on the contrapositive of the above claim. That is, if we can find an a such that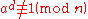
and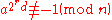
for all 
then n is not prime. We call a a witness
for the compositeness of n (sometimes misleadingly called a strong witness, although it is a certain proof of this fact). Otherwise a is called a strong liar, and n is a strong probable prime
to base a. The term "strong liar" refers to the case where n is composite but nevertheless the equations hold as they would for a prime.
For every odd composite n, there are many witnesses a. However, no simple way of generating such an a is known. The solution is to make the test probabilistic: we choose nonzero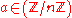
randomly, and check whether or not it is a witness for the compositeness of n. If n is composite, most of the choices for a will be witnesses, and the test will detect n as composite with high probability. There is, nevertheless, a small chance that we are unlucky and hit an a which is a strong liar for n. We may reduce the probability of such error by repeating the test for several independently chosen a.
Since 220 ≡ −1 mod n, either 221 is prime, or 174 is a strong liar for 221. We try another random a, this time choosing a=137:
Hence 137 is a witness for the compositeness of 221, and 174 was in fact a strong liar. Note that this tells us nothing about the factors of 221 (which are 13 and 17).
as follows:
Input: n > 3, an odd integer to be tested for primality;
Input: k, a parameter that determines the accuracy of the test
Output: composite if n is composite, otherwise probably prime
write n − 1 as 2s·d with d odd by factoring powers of 2 from n − 1
LOOP: repeat k times:
pick a random integer a in the range [2, n − 2]
x ← ad mod n
if x = 1 or x = n − 1 then do next LOOP
for r = 1 .. s − 1
x ← x2 mod n
if x = 1 then return composite
if x = n − 1 then do next LOOP
return composite
return probably prime
Using modular exponentiation
by repeated squaring
, the running time of this algorithm is O
(k log3 n), where k is the number of different values of a we test; thus this is an efficient, polynomial-time algorithm. FFT
-based multiplication can push the running time down to = Õ(k log2 n).
In the case that the algorithm returns "composite" because x = 1, it has also discovered that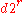
is (an odd multiple of) the order
of a — a fact which can (as in Shor's algorithm
) be used to factorize n, since n then divides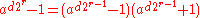
but not either factor by itself. The reason Miller–Rabin does not yield a probabilistic factorization
algorithm is that if
(i.e., n is not a pseudoprime
to base a) then no such information is obtained about the period of a, and the second "return composite" is taken.
On average the probability that a composite number is declared probably prime is significantly smaller than 4−k. Damgård
, Landrock and Pomerance
compute some explicit bounds. Such bounds can, for example, be used to generate primes; however, they should not be used to verify primes with unknown origin, since in cryptographic
applications an adversary might try to send you a pseudoprime
in a place where a prime number is required. In such cases, only the error bound of 4−k can be relied upon.
If the tested number n is composite, the strong liars a coprime to n are contained in a proper subgroup
of the group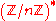
, which means that if we test all a from a set which generates
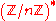, one of them must be a witness for the compositeness of n. Assuming the truth of the generalized Riemann hypothesis
(GRH), it is known that the group is generated by its elements smaller than O((log n)2), which was already noted by Miller. The constant involved in the Big O notation
was reduced to 2 by Eric Bach
. This leads to the following conditional primality testing algorithm:
Input: n > 1, an odd integer to test for primality.
Output: composite if n is composite, otherwise prime
write n−1 as 2s·d by factoring powers of 2 from n−1
repeat for all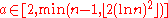
:
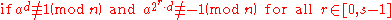
then return composite
return prime
The running time of the algorithm is Õ((log n)4). The full power of the generalized Riemann hypothesis is not needed to ensure the correctness of the test: as we deal with subgroups of even index
, it suffices to assume the validity of GRH for quadratic
Dirichlet character
s.
This algorithm is not used in practice, as it is much slower than the randomized version of the Miller-Rabin test. For theoretical purposes, it was superseded by the AKS primality test
, which does not rely on unproven assumptions.
When the number n to be tested is small, trying all a < 2(ln n)2 is not necessary, as much smaller sets of potential witnesses are known to suffice. For example, Pomerance, Selfridge and Wagstaff and Jaeschke have verified that
Other criteria of this sort exist and these results give very fast deterministic primality tests for numbers in the appropriate range, without any assumptions.
There is a small list of potential witnesses for every possible input size (at most n values for n-bit numbers). However, no finite set of bases is sufficient for all composite numbers. Alford, Granville, and Pomerance have shown that there exist infinitely many composite numbers n whose smallest compositeness witness is at least (ln n)1/(3ln ln ln n). They also argue heuristically that the smallest number w such that every composite number below n has a compositeness witness less than w should be of order
(log n log log n).
Primality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
: an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
which determines whether a given number is prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
,
similar to the Fermat primality test
Fermat primality test
The Fermat primality test is a probabilistic test to determine if a number is probable prime.-Concept:Fermat's little theorem states that if p is prime and 1 \le a...
and the Solovay–Strassen primality test. Its original version, due to Gary L. Miller
Gary Miller (professor)
Gary Lee Miller is a professor of Computer Science at Carnegie Mellon University, Pittsburgh, United States. In 2003, he won the ACM Paris Kanellakis Award for the Miller–Rabin primality test. He was also made an ACM Fellow in 2002....
, is deterministic
Deterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
, but the determinism relies on the unproven generalized Riemann hypothesis
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
; Michael O. Rabin
Michael O. Rabin
Michael Oser Rabin , is an Israeli computer scientist and a recipient of the Turing Award.- Biography :Rabin was born in 1931 in Breslau, Germany, , the son of a rabbi. In 1935, he emigrated with his family to Mandate Palestine...
modified it to obtain an unconditional probabilistic algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
.
Concepts
Just like the Fermat and Solovay–Strassen tests, the Miller–Rabin test relies on an equality or set of equalities that hold true for prime values, then checks whether or not they hold for a number that we want to test for primality.First, a lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
about square roots of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
in the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
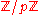, where p is prime and p > 2. Certainly 1 and −1 always yield 1 when squared mod p; call these trivialTrivial (mathematics)
In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s of 1. There are no nontrivial square roots of 1 mod p (a special case of the result that, in a field, a polynomial has no more zeroes than its degree). To show this, suppose that x is a square root of 1 mod p. Then:
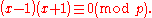
In other words, p divides the product
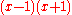. It thus divides one of the factors and it follows that x is either congruent to 1 or −1 mod p.Now, let n be an odd prime. Then n−1 is even and we can write it as 2s·d, where s and d are positive integers (d is odd). For each
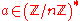, eitheror
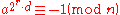for some To show that one of these must be true, recall Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
:
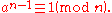
By the lemma above, if we keep taking square roots of an − 1, we will get either 1 or −1. If we get −1 then the second equality holds and we are done. If we never get −1, then when we have taken out every power of 2, we are left with the first equality.
The Miller–Rabin primality test is based on the contrapositive of the above claim. That is, if we can find an a such that
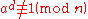
and
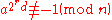for all then n is not prime. We call a a witness
Witness (mathematics)
In mathematical logic, a witness is a specific value t to be substituted for variable x of an existential statement of the form ∃x φ such that φ is true.- Examples :...
for the compositeness of n (sometimes misleadingly called a strong witness, although it is a certain proof of this fact). Otherwise a is called a strong liar, and n is a strong probable prime
Probable prime
In number theory, a probable prime is an integer that satisfies a specific condition also satisfied by all prime numbers. Different types of probable primes have different specific conditions...
to base a. The term "strong liar" refers to the case where n is composite but nevertheless the equations hold as they would for a prime.
For every odd composite n, there are many witnesses a. However, no simple way of generating such an a is known. The solution is to make the test probabilistic: we choose nonzero
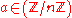randomly, and check whether or not it is a witness for the compositeness of n. If n is composite, most of the choices for a will be witnesses, and the test will detect n as composite with high probability. There is, nevertheless, a small chance that we are unlucky and hit an a which is a strong liar for n. We may reduce the probability of such error by repeating the test for several independently chosen a.Example
Suppose we wish to determine if n = 221 is prime. We write n − 1 = 220 as 22·55, so that we have s = 2 and d = 55. We randomly select a number a such that a < n, say a = 174. We proceed to compute:- a20·d mod n = 17455 mod 221 = 47 ≠ 1, n − 1
- a21·d mod n = 174110 mod 221 = 220 = n − 1.
Since 220 ≡ −1 mod n, either 221 is prime, or 174 is a strong liar for 221. We try another random a, this time choosing a=137:
- a20·d mod n = 13755 mod 221 = 188 ≠ 1, n − 1
- a21·d mod n = 137110 mod 221 = 205 ≠ n − 1.
Hence 137 is a witness for the compositeness of 221, and 174 was in fact a strong liar. Note that this tells us nothing about the factors of 221 (which are 13 and 17).
Algorithm and running time
The algorithm can be written in pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
as follows:
Input: n > 3, an odd integer to be tested for primality;
Input: k, a parameter that determines the accuracy of the test
Output: composite if n is composite, otherwise probably prime
write n − 1 as 2s·d with d odd by factoring powers of 2 from n − 1
LOOP: repeat k times:
pick a random integer a in the range [2, n − 2]
x ← ad mod n
if x = 1 or x = n − 1 then do next LOOP
for r = 1 .. s − 1
x ← x2 mod n
if x = 1 then return composite
if x = n − 1 then do next LOOP
return composite
return probably prime
Using modular exponentiation
Modular exponentiation
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
by repeated squaring
Exponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
, the running time of this algorithm is O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(k log3 n), where k is the number of different values of a we test; thus this is an efficient, polynomial-time algorithm. FFT
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
-based multiplication can push the running time down to = Õ(k log2 n).
In the case that the algorithm returns "composite" because x = 1, it has also discovered that
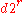is (an odd multiple of) the orderOrder (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of a — a fact which can (as in Shor's algorithm
Shor's algorithm
Shor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
) be used to factorize n, since n then divides
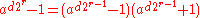but not either factor by itself. The reason Miller–Rabin does not yield a probabilistic factorizationInteger factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
algorithm is that if
(i.e., n is not a pseudoprimePseudoprime
In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.- Definition :...
to base a) then no such information is obtained about the period of a, and the second "return composite" is taken.
Accuracy of the test
The more bases a we test, the better the accuracy of the test. It can be shown that for any odd composite n, at least ¾ of the bases a are witnesses for the compositeness of n. The Miller–Rabin test is strictly stronger than the Solovay–Strassen primality test in the sense that for every composite n, the set of strong liars for n is a subset of the set of Euler liars for n, and for many n, the subset is proper. If n is composite then the Miller–Rabin primality test declares n probably prime with a probability at most 4−k. On the other hand, the Solovay–Strassen primality test declares n probably prime with a probability at most 2−k.On average the probability that a composite number is declared probably prime is significantly smaller than 4−k. Damgård
Ivan Damgård
Ivan Bjerre Damgård is a Danish cryptographer and currently a professor at the Department of Computer Science , Aarhus University, Denmark....
, Landrock and Pomerance
Carl Pomerance
Carl Bernard Pomerance is a well-known number theorist. He attended college at Brown University and later received his Ph.D. from Harvard University in 1972 with a dissertation proving that any odd perfect number has at least 7 distinct prime factors. He immediately joined the faculty at the...
compute some explicit bounds. Such bounds can, for example, be used to generate primes; however, they should not be used to verify primes with unknown origin, since in cryptographic
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
applications an adversary might try to send you a pseudoprime
Pseudoprime
In number theory, the Fermat pseudoprimes make up the most important class of pseudoprimes that come from Fermat's little theorem.- Definition :...
in a place where a prime number is required. In such cases, only the error bound of 4−k can be relied upon.
Deterministic variants of the test
The Miller–Rabin algorithm can be made deterministic by trying all possible a below a certain limit. The problem in general is to set the limit so that the test is still reliable.If the tested number n is composite, the strong liars a coprime to n are contained in a proper subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the group
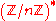, which means that if we test all a from a set which generatesGenerating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
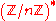, one of them must be a witness for the compositeness of n. Assuming the truth of the generalized Riemann hypothesisGeneralized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
(GRH), it is known that the group is generated by its elements smaller than O((log n)2), which was already noted by Miller. The constant involved in the Big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
was reduced to 2 by Eric Bach
Eric Bach
Eric Bach is an American computer scientist who has made contributions to computational number theory. Bach did his undergraduate studies at the University of Michigan, Ann Arbor, and got his Ph.D. in computer science from the University of California, Berkeley, in 1984 under the supervision of...
. This leads to the following conditional primality testing algorithm:
Input: n > 1, an odd integer to test for primality.
Output: composite if n is composite, otherwise prime
write n−1 as 2s·d by factoring powers of 2 from n−1
repeat for all
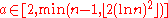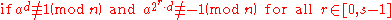
:then return composite
return prime
The running time of the algorithm is Õ((log n)4). The full power of the generalized Riemann hypothesis is not needed to ensure the correctness of the test: as we deal with subgroups of even index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
, it suffices to assume the validity of GRH for quadratic
Legendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
Dirichlet character
Dirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
s.
This algorithm is not used in practice, as it is much slower than the randomized version of the Miller-Rabin test. For theoretical purposes, it was superseded by the AKS primality test
AKS primality test
The AKS primality test is a deterministic primality-proving algorithm created and published by three Indian Institute of Technology Kanpur computer scientists, Manindra Agrawal, Neeraj Kayal, and Nitin Saxena, on August 6, 2002, in a paper titled "PRIMES is in P"...
, which does not rely on unproven assumptions.
When the number n to be tested is small, trying all a < 2(ln n)2 is not necessary, as much smaller sets of potential witnesses are known to suffice. For example, Pomerance, Selfridge and Wagstaff and Jaeschke have verified that
- if n < 1,373,653, it is enough to test a = 2 and 3;
- if n < 9,080,191, it is enough to test a = 31 and 73;
- if n < 4,759,123,141, it is enough to test a = 2, 7, and 61;
- if n < 2,152,302,898,747, it is enough to test a = 2, 3, 5, 7, and 11;
- if n < 3,474,749,660,383, it is enough to test a = 2, 3, 5, 7, 11, and 13;
- if n < 341,550,071,728,321, it is enough to test a = 2, 3, 5, 7, 11, 13, and 17.
Other criteria of this sort exist and these results give very fast deterministic primality tests for numbers in the appropriate range, without any assumptions.
There is a small list of potential witnesses for every possible input size (at most n values for n-bit numbers). However, no finite set of bases is sufficient for all composite numbers. Alford, Granville, and Pomerance have shown that there exist infinitely many composite numbers n whose smallest compositeness witness is at least (ln n)1/(3ln ln ln n). They also argue heuristically that the smallest number w such that every composite number below n has a compositeness witness less than w should be of order
(log n log log n).External links
- Interactive Online Implementation of the Deterministic Variant (stepping through the algorithm step-by-step)
- Applet (German)
- Miller-Rabin primality test in JavaScript using arbitrary precision arithmetic