Metamath
Encyclopedia
Metamath is a computer-assisted proof checker. It has no specific logic embedded and can simply be regarded as a device to apply inference rules to formulas. Simplicity is the master concept in the design of Metamath: the language of Metamath, employed to state the definitions, axioms, inference rules and theorems is only composed of a handful of keywords and all the proofs are checked using one simple algorithm based on the substitution of variables (with optional provisos for what variables must remain distinct after a substitution is made). This "substitution" is just the simple replacement of a variable with an expression and not the proper substitution described in works on predicate calculus.
Metamath has been used to develop set.mm, a human-readable database containing over 15000 fully formal proofs of mathematical theorems built upon ZFC set theory. Those proofs may be browsed on the internet using an interface called Metamath Proof Explorer. New theorems are added to set.mm daily; a table of the most recent proofs is maintained.
. In contrast, it is largely incompatible with logical systems which uses other things than formulas and inference rules. The original natural deduction system (due to Gerhard Gentzen
), which uses an extra stack
, is an example of a system that cannot be implemented with Metamath. In the case of natural deduction however it is possible to append the stack to the formulas (transforming the natural deduction formulas into a sort of sequent) so that Metamath's requirements are met.
What makes Metamath so generic is its substitution algorithm. This algorithm makes no assumption about the used logic and only checks the substitutions of variables are correctly done.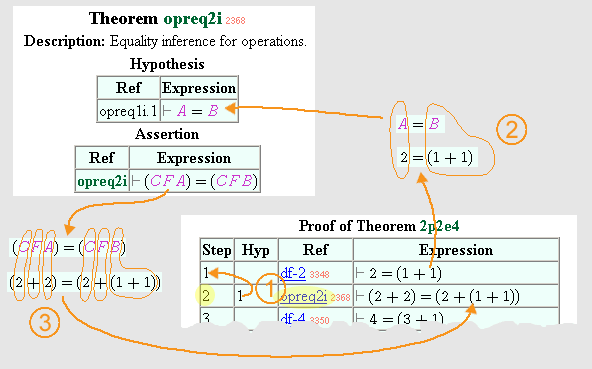
So here is a detailed example of how this algorithm works. Steps 1 and 2 of the theorem 
. It is the conclusion of the theorem 
, then 
. This theorem would never appear under this cryptic form in a textbook but its literate formulation is banal: when two quantities are equal , one can replace one by the other in an operation. To check the proof Metamath attempts to unify 
with 
. There is only one way to do so: unifying 
with 
, 
with 
, 
with 
and 
with 
. So now Metamath uses the premise of 
. As a consequence of its previous computation, Metamath knows that 
should be substituted by 
and 
by 
. The premise 
becomes 
and thus step 1 is therefore generated. In its turn step 1 is unified with
There is however some complications that are not shown on the picture. When Metamath unifies
with 
it has to check that the syntactical rules are respected. In fact 
has the type 
is also typed
The above explanation may let suppose that formulas are stored by Metamath. In fact nothing of that sort exists. Metamath only stores the conclusion and the premises of the proven theorem and the list of the names of the theorems used by the proof and nothing more. But since it is possible, with the substitution algorithm, to generate the conclusion from the premises nothing more is required.
Metamath tokens carefully follow the definition of a formal system. Typically a formal system is a quadruplet
where 
is a finite set of symbols, 
a set of formulas ( syntactic rules allow to decide if a string of symbols is a formula or not ), 
a set of axioms, 
a set of inference rules.
It is pretty straightforward to connect the tokens of Metamath with the abstract definition of a formal system. The finite set of symbols
is declared using the 
of formulas), the set 
of axioms and the set 
of inference rules are declared using the
We can notice that in Metamath syntactic rules, axioms and inference rules use the same token (namely the
, 
, 
) . This at least shows that in Metamath there is no essential separation between the syntactical analysis and the properly logic treatment nor any separation between axioms and inference rules. This economical point of view is in many ways proper to Metamath where things that are often thought (perhaps too strongly) as being different are in fact confused (this tendency can be met in other places: for instance see below the remark definitions).
may be replaced (and thus eliminated) by the definiens
. For instance
. Specific operators are frequently used in textbooks to express definitions (such as a biimplication sign with a small "def" above the arrow) but the equivalence operator is appropriate and it also allows to use the normal propositional calculus to manage the formulas (a specific operator wouldn't be as economical).
Theorems and proof : A proof is associated with a theorem using the
Type of variables : In Metamath variables are typed with the
Schemes : Whereas a formal description of logic uses formulas with actual variables, Metamath uses schemes. The variables of Metamath's theorem schemes are generic variables, and any appropriate substitution can be made for them. The fact that a theorem is a scheme means that in fact it refers to a whole set of theorems. The theorem
can be used for 
, 
or 
for instance. Which after all is the usual way to read a theorem.
Symbols : since Metamath database are intended to be human-readable, Metamath uses ASCII
to denote mathematical symbols. In set.mm the notation is occasionally different from standard. For example,
in a mathematics textbook), and 
in a textbook).
set.mm is by far the biggest database written for Metamath, but there is also a formalization (by Robert Solovay) of Peano arithmetic called peano.mm (included in metamath.zip) and a formalization of natural deduction
called nat.mm. There is a database based on the formal system MIU presented in Gödel, Escher, Bach
. Raph Levien has also designed several databases for his Ghilbert program.
set.mm has been maintained for more than ten years now (the first proofs in set.mm are dated August 1993). It is mainly a work by Norman Megill but there are also proofs made by other participants. Technically speaking set.mm develops—in the Hilbert style—ZFC set theory with the addition of the Grothendieck-Tarski axiom (to manage categories
). The underlying logic is classical propositional calculus
and classical predicate calculus with equality.
set.mm is a valuable tool to understand how well-known set theory concepts such as classes, power sets, union, relations, functions, equivalence classes and so on are derived from the axioms.
However set.mm doesn't stop at these basic notions but explores more elaborated theories.
Cantor concepts such as ordinal and cardinal numbers, equinumerosity or aleph function are defined.
Integers and natural numbers are constructed along with traditional arithmetic tools such as operations
, recursion
or induction
.
The real
and complex number
s are constructed from Dedekind cut
s, and the concepts of sequence
, limit of a sequence
, sum of a series and so on are developed for them. The concept of integral
is still missing.
Square root, exponentiation, exponential
and trigonometric function
s are implemented.
General topology
is currently developed: topological spaces, closed and open sets, neighborhood, limit point, continuous function, Hausdorff spaces, metric spaces, Cauchy sequences have been defined.
One can also find some theorems of algebra concerning groups
, rings
, vector spaces and Hilbert spaces.
theory. Those theorems are included in set.mm. They are not shown in the Metamath Proof Explorer because they have been developed by adding extra axioms to the standard axioms of set.mm. ZFC is weakened by this adding which explains why the resulting proofs are shown in a separate Explorer. This adding (justified by historical opportunity reasons) is theoretically useless since the concept of Hilbert space can be designed with the standard ZFC axioms.
theorems can be found in the database ql.mm. The Quantum Logic Explorer is an internet interface to this database.
's time. In Metamath, the method of proof is the symbolic, analytical method of proof invented by Aristotle
, Leibniz
, Peano
and Frege
. Thus, Metamath is unsuitable for school exercises. To speak simply, the proofs in Metamath are much too detailed to be used with ease in school. However, set.mm can be used in a school context as an example of a symbolic system that is big enough to be interesting. set.mm can also be useful because its detailed, symbolic, unambiguous definitions can resolve confusion with textbook definitions. Students may also appreciate the rigor of the Metamath Proof Explorer; no steps are skipped, no assumption left unstated, and no proofs are left "to the reader."
The Proof Explorer references many text books that can be used in conjunction with Metamath. Thus, people interested in studying mathematics can use Metamath in connection with these books.
has implemented what might be the smallest proof checker in the world, mmverify.py, at only 500 lines of Python code.
Ghilbert is a similar though more elaborate language based on mmverify.py. Levien would like to implement a system where several people could collaborate together and his work is emphasizing modularity and connection between small theories.
Using Levien seminal works, many other implementations of the Metamath design principles have been implemented for a broad variety of languages. Juha Arpiainen has implemented his own proof checker in Common Lisp
called Bourbaki and Marnix Klooster has coded a proof checker in Haskell
called Hmm.
Although they all use the overall Metamath approach to formal system checker coding, they also implement new concepts of their own.
There is also a project by William Hale to add a graphical user interface to Metamath called Mmide. Paul Chapman in its turn is working on a new proof browser, which has highlighting that allows you to see the referenced theorem before and after the substitution was made.
Metamath has been used to develop set.mm, a human-readable database containing over 15000 fully formal proofs of mathematical theorems built upon ZFC set theory. Those proofs may be browsed on the internet using an interface called Metamath Proof Explorer. New theorems are added to set.mm daily; a table of the most recent proofs is maintained.
A generic proof checker
Even if Metamath is used for mathematical proof checking, its algorithm is so general we can extend the field of its usage. In fact Metamath could be used with every sort of formal systems: the checking of a computer program could be considered (even if Metamath's low level would make it difficult); it could possibly even be a syntactic checker for a natural language (same remark). Because Metamath has a very generic concept of what a proof is (namely a tree of formulas connected by inference rules) and no specific logic is embedded in the software, Metamath can be used with species of logic as different as Hilbert-style logics or sequents-based logics or even with lambda calculusLambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
. In contrast, it is largely incompatible with logical systems which uses other things than formulas and inference rules. The original natural deduction system (due to Gerhard Gentzen
Gerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
), which uses an extra stack
Stack (data structure)
In computer science, a stack is a last in, first out abstract data type and linear data structure. A stack can have any abstract data type as an element, but is characterized by only three fundamental operations: push, pop and stack top. The push operation adds a new item to the top of the stack,...
, is an example of a system that cannot be implemented with Metamath. In the case of natural deduction however it is possible to append the stack to the formulas (transforming the natural deduction formulas into a sort of sequent) so that Metamath's requirements are met.
What makes Metamath so generic is its substitution algorithm. This algorithm makes no assumption about the used logic and only checks the substitutions of variables are correctly done.
2p2e4 in set.mm are depicted left. Let's explain how Metamath uses its substitution algorithm to check that step 2 is the logical consequence of step 1 when you use the theorem opreq2i. Step 2 states that . It is the conclusion of the theorem opreq2i. The theorem opreq2i states that if , then . This theorem would never appear under this cryptic form in a textbook but its literate formulation is banal: when two quantities are equal , one can replace one by the other in an operation. To check the proof Metamath attempts to unify with . There is only one way to do so: unifying with , with , with and with . So now Metamath uses the premise of opreq2i. This premise states that . As a consequence of its previous computation, Metamath knows that should be substituted by and by . The premise becomes and thus step 1 is therefore generated. In its turn step 1 is unified with df-2. df-2 is the definition of the number 2 and states that 2 = ( 1 + 1 ). Here the unification is simply a matter of constants and is straightforward (no problem of variables to substitute). So the verification is finished and these two steps of the proof of 2p2e4 are correct.There is however some complications that are not shown on the picture. When Metamath unifies
with it has to check that the syntactical rules are respected. In fact has the type class thus Metamath has to check that is also typed class This is done using the same sort of unification described in the paragraph above.The above explanation may let suppose that formulas are stored by Metamath. In fact nothing of that sort exists. Metamath only stores the conclusion and the premises of the proven theorem and the list of the names of the theorems used by the proof and nothing more. But since it is possible, with the substitution algorithm, to generate the conclusion from the premises nothing more is required.
The Metamath language
The Metamath language is based on a very small number of tokens. There are two tokens to declare the symbols of the logic: one to declare the constants ($c) and one to declare the variables ($v). Syntactic rules and axioms are declared using the $a token, and inference rules are declared using $a for the conclusion and $e for the premises. Eventually, $p is used to declare a theorem and its proof.Metamath tokens carefully follow the definition of a formal system. Typically a formal system is a quadruplet
where is a finite set of symbols, a set of formulas ( syntactic rules allow to decide if a string of symbols is a formula or not ), a set of axioms, a set of inference rules.It is pretty straightforward to connect the tokens of Metamath with the abstract definition of a formal system. The finite set of symbols
is declared using the $c and the $v tokens. The syntactic rules (used to define the set of formulas), the set of axioms and the set of inference rules are declared using the $a token.We can notice that in Metamath syntactic rules, axioms and inference rules use the same token (namely the
$a token). This feature is not obvious if one refers to the definition of a formal system above since this definition uses three different sets (, , ) . This at least shows that in Metamath there is no essential separation between the syntactical analysis and the properly logic treatment nor any separation between axioms and inference rules. This economical point of view is in many ways proper to Metamath where things that are often thought (perhaps too strongly) as being different are in fact confused (this tendency can be met in other places: for instance see below the remark definitions).Further remarks
Definitions : In Metamath a definition is an axiom, and the$a token is used to declare a definition as it is used to declare an axiom. The only difference lies in the fact that in definitions the definiendumDefinition
A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
may be replaced (and thus eliminated) by the definiens
Definition
A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
. For instance
A =/= B is defined by ( A =/= B <-> -. A = B ) (-. meaning "not"). So if we consider the theorem |- A =/= { A } and if we replace the definiendum =/= by the definiens ( -. A = B we get -. A = { A }. Then we can continue (replacing { A } by its definition) until there are only primitive symbols (i.e. equality, the "belong to" relation, quantifiers and individual variables. The symbol used by Metamath to link definiens and definiendum is the equivalence operatorIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
. Specific operators are frequently used in textbooks to express definitions (such as a biimplication sign with a small "def" above the arrow) but the equivalence operator is appropriate and it also allows to use the normal propositional calculus to manage the formulas (a specific operator wouldn't be as economical).
Theorems and proof : A proof is associated with a theorem using the
$p token. In theoretical logic, a proof is a list of formulas, each of which are either axioms or the consequences of the application of an inference rule to previous formulas in the list. Metamath allows the use of other theorems that have already been proved and supports the use of hypotheses (using the $e statement). Only the names (not the effective formulas) of the used theorems and axioms are stored in a Metamath proof.Type of variables : In Metamath variables are typed with the
$f statement. In set.mm, for instance, there are only three types: propositional, individual and class variables.Schemes : Whereas a formal description of logic uses formulas with actual variables, Metamath uses schemes. The variables of Metamath's theorem schemes are generic variables, and any appropriate substitution can be made for them. The fact that a theorem is a scheme means that in fact it refers to a whole set of theorems. The theorem
can be used for , or for instance. Which after all is the usual way to read a theorem.Symbols : since Metamath database are intended to be human-readable, Metamath uses ASCII
ASCII
The American Standard Code for Information Interchange is a character-encoding scheme based on the ordering of the English alphabet. ASCII codes represent text in computers, communications equipment, and other devices that use text...
to denote mathematical symbols. In set.mm the notation is occasionally different from standard. For example,
[ y / x ] ph might denote the formula that corresponds to ph when x has been properly substituted by y (and which is usually written in a mathematics textbook), and ( F ` B ) might denote the value taken by the function F when applied to B (it would be coded in a textbook).Databases
Metamath comes along with two main databases set.mm and ql.mm. set.mm stores theorems concerning ZFC theory and ql.mm develops a set of quantum logic theorems. Three internet interfaces (the Metamath Proof Explorer, the Hilbert Space Explorer and the Quantum Logic Explorer) are provided to explore these two databases in a human friendly way.set.mm is by far the biggest database written for Metamath, but there is also a formalization (by Robert Solovay) of Peano arithmetic called peano.mm (included in metamath.zip) and a formalization of natural deduction
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
called nat.mm. There is a database based on the formal system MIU presented in Gödel, Escher, Bach
Gödel, Escher, Bach
Gödel, Escher, Bach: An Eternal Golden Braid is a book by Douglas Hofstadter, described by his publishing company as "a metaphorical fugue on minds and machines in the spirit of Lewis Carroll"....
. Raph Levien has also designed several databases for his Ghilbert program.
Metamath Proof Explorer
One of the seminal ideas that lead Megill to design Metamath was the desire to precisely determine the correctness of some proofs ("I enjoy abstract mathematics, but I sometimes get lost in a barrage of definitions and start to lose confidence that my proofs are correct."), we can also think that the spirit of the Encyclopedia animates the growing up of Metamath and its most important database (called set.mm). Reading set.mm we may have sometimes the impression that the ambition of its author is essentially to add all the mathematics one theorem after the other.set.mm has been maintained for more than ten years now (the first proofs in set.mm are dated August 1993). It is mainly a work by Norman Megill but there are also proofs made by other participants. Technically speaking set.mm develops—in the Hilbert style—ZFC set theory with the addition of the Grothendieck-Tarski axiom (to manage categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
). The underlying logic is classical propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
and classical predicate calculus with equality.
set.mm is a valuable tool to understand how well-known set theory concepts such as classes, power sets, union, relations, functions, equivalence classes and so on are derived from the axioms.
However set.mm doesn't stop at these basic notions but explores more elaborated theories.
Cantor concepts such as ordinal and cardinal numbers, equinumerosity or aleph function are defined.
Integers and natural numbers are constructed along with traditional arithmetic tools such as operations
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
, recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
or induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
.
The real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s are constructed from Dedekind cut
Dedekind cut
In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
s, and the concepts of sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
, limit of a sequence
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
, sum of a series and so on are developed for them. The concept of integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
is still missing.
Square root, exponentiation, exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
and trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s are implemented.
General topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
is currently developed: topological spaces, closed and open sets, neighborhood, limit point, continuous function, Hausdorff spaces, metric spaces, Cauchy sequences have been defined.
One can also find some theorems of algebra concerning groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, vector spaces and Hilbert spaces.
Hilbert Space Explorer
The Hilbert Space Explorer presents more than 1,000 theorems pertaining to the Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
theory. Those theorems are included in set.mm. They are not shown in the Metamath Proof Explorer because they have been developed by adding extra axioms to the standard axioms of set.mm. ZFC is weakened by this adding which explains why the resulting proofs are shown in a separate Explorer. This adding (justified by historical opportunity reasons) is theoretically useless since the concept of Hilbert space can be designed with the standard ZFC axioms.
Quantum Logic Explorer
Quantum logicQuantum logic
In quantum mechanics, quantum logic is a set of rules for reasoning about propositions which takes the principles of quantum theory into account...
theorems can be found in the database ql.mm. The Quantum Logic Explorer is an internet interface to this database.
Annexe 1: Pedagogy
The method of proof used by Metamath is far different from what is used in a school context. In schools what is required is the literate, synthetic method of proof developed by mathematicians since EuclidEuclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's time. In Metamath, the method of proof is the symbolic, analytical method of proof invented by Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
, Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
, Peano
Giuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
and Frege
Gottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
. Thus, Metamath is unsuitable for school exercises. To speak simply, the proofs in Metamath are much too detailed to be used with ease in school. However, set.mm can be used in a school context as an example of a symbolic system that is big enough to be interesting. set.mm can also be useful because its detailed, symbolic, unambiguous definitions can resolve confusion with textbook definitions. Students may also appreciate the rigor of the Metamath Proof Explorer; no steps are skipped, no assumption left unstated, and no proofs are left "to the reader."
The Proof Explorer references many text books that can be used in conjunction with Metamath. Thus, people interested in studying mathematics can use Metamath in connection with these books.
Proof checkers
Using the design ideas implemented in Metamath, Raph LevienRaph Levien
Raphael Levien is an influential member of the free software developer community, through his creation of the Advogato virtual community and his work with the free software branch of Ghostscript. He is currently employed by Google...
has implemented what might be the smallest proof checker in the world, mmverify.py, at only 500 lines of Python code.
Ghilbert is a similar though more elaborate language based on mmverify.py. Levien would like to implement a system where several people could collaborate together and his work is emphasizing modularity and connection between small theories.
Using Levien seminal works, many other implementations of the Metamath design principles have been implemented for a broad variety of languages. Juha Arpiainen has implemented his own proof checker in Common Lisp
Common Lisp
Common Lisp, commonly abbreviated CL, is a dialect of the Lisp programming language, published in ANSI standard document ANSI INCITS 226-1994 , . From the ANSI Common Lisp standard the Common Lisp HyperSpec has been derived for use with web browsers...
called Bourbaki and Marnix Klooster has coded a proof checker in Haskell
Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
called Hmm.
Although they all use the overall Metamath approach to formal system checker coding, they also implement new concepts of their own.
Editors
Mel O'Cat designed a system called Mmj2 which provides a graphic user interface for proof entry. The initial aim of Mel O'Cat was to allow the user to enter the proofs by simply typing the formulas and letting Mmj2 find the appropriate inference rules to connect them. In Metamath on the contrary you may only enter the theorems names. You may not enter the formulas directly. Mmj2 has also the possibility to enter the proof forward or backward (Metamath only allows to enter proof backward). Moreover Mmj2 has a real grammar parser (unlike Metamath). This technical difference brings more comfort to the user. In particular Metamath sometimes hesitates between several formulas analyzes (most of them being meaningless) and asks the user to choose. In Mmj2 this limitation no longer exists.There is also a project by William Hale to add a graphical user interface to Metamath called Mmide. Paul Chapman in its turn is working on a new proof browser, which has highlighting that allows you to see the referenced theorem before and after the substitution was made.