Lagged Fibonacci generator
Encyclopedia
A Lagged Fibonacci generator (LFG) is an example of a pseudorandom number generator
. This class of random number generator is aimed at being an improvement on the 'standard' linear congruential generator
. These are based on a generalisation of the Fibonacci sequence.
The Fibonacci sequence may be described by the recurrence relation
:
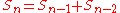
Hence, the new term is the sum of the last two terms in the sequence. This can be generalised to the sequence:
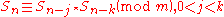
In which case, the new term is some combination of any two previous terms. m is usually a power of 2 (m = 2M), often 232 or 264. The
operator denotes a general binary operation
. This may be either addition, subtraction, multiplication, or the bitwise
arithmetic exclusive-or operator (XOR). The theory of this type of generator is rather complex, and it may not be sufficient simply to choose random values for j and k. These generators also tend to be very sensitive to initialisation.
Generators of this type employ k words of state (they 'remember' the last k values).
If the operation used is addition, then the generator is described as an Additive Lagged Fibonacci Generator or ALFG, if multiplication is used, it is a Multiplicative Lagged Fibonacci Generator or MLFG, and if the XOR operation is used, it is called a Two-tap generalised feedback shift register or GFSR. The Mersenne twister algorithm is a variation on a GFSR. The GFSR is also related to the Linear Feedback Shift Register, or LFSR.
For the generator to achieve this maximum period, the polynomial:
must be primitive
over the integers mod 2. Values of j and k satisfying this constraint have been published in the literature. Popular pairs are:
Another list of possible values for j and k is on page 29 of volume 2 of The Art of Computer Programming
:
, (38,89), (37,100), (30,127), (83,258), (107,378), (273,607), (1029,2281), (576,3217), (4187,9689), (7083,19937), (9739,23209)
Note that the smaller number have short periods (only a few "random" numbers are generated before the first "random" number is repeated and the sequence restarts).
It is required that at least one of the first k values chosen to initialise the generator be odd.
It has been suggested that good ratios between j and k are approximately the golden ratio
.
observed very poor behavior with R(24,55) and smaller generators, and advised against using generators of this type altogether. ... The basic problem of two-tap generators R(a, b) is that they have a built-in three-point correlation between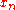
, 
, and 
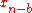, simply given by the generator itself ... While these correlations are spread over the size 
of the generator itself, they can evidently still lead to significant errors.".
The initialization of LFGs is a very complex problem. The output of LFGs is very sensitive to initial conditions, and statistical defects may appear initially but also periodically in the output sequence unless extreme care is taken . Another potential problem with LFGs is that the mathematical theory behind them is incomplete, making it necessary to rely on statistical tests rather than theoretical performance.
Pseudorandom number generator
A pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
. This class of random number generator is aimed at being an improvement on the 'standard' linear congruential generator
Linear congruential generator
A Linear Congruential Generator represents one of the oldest and best-known pseudorandom number generator algorithms. The theory behind them is easy to understand, and they are easily implemented and fast....
. These are based on a generalisation of the Fibonacci sequence.
The Fibonacci sequence may be described by the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
:
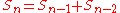
Hence, the new term is the sum of the last two terms in the sequence. This can be generalised to the sequence:
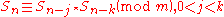
In which case, the new term is some combination of any two previous terms. m is usually a power of 2 (m = 2M), often 232 or 264. The
operator denotes a general binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
. This may be either addition, subtraction, multiplication, or the bitwise
Bitwise
Bitwise may refer to:* Bitwise operation, a basic function in computer programming* Bitwise IIT Kharagpur, an algorithm-intensive programming contest by CSE IIT Kharagpur...
arithmetic exclusive-or operator (XOR). The theory of this type of generator is rather complex, and it may not be sufficient simply to choose random values for j and k. These generators also tend to be very sensitive to initialisation.
Generators of this type employ k words of state (they 'remember' the last k values).
If the operation used is addition, then the generator is described as an Additive Lagged Fibonacci Generator or ALFG, if multiplication is used, it is a Multiplicative Lagged Fibonacci Generator or MLFG, and if the XOR operation is used, it is called a Two-tap generalised feedback shift register or GFSR. The Mersenne twister algorithm is a variation on a GFSR. The GFSR is also related to the Linear Feedback Shift Register, or LFSR.
Properties of lagged Fibonacci generators
Lagged Fibonacci generators have a maximum period of (2k - 1)*2M-1 if addition or subtraction is used, and (2k-1)*k if exclusive-or operations are used to combine the previous values. If, on the other hand, multiplication is used, the maximum period is (2k - 1)*2M-3, or 1/4 of period of the additive case.For the generator to achieve this maximum period, the polynomial:
- y = xk + xj + 1
must be primitive
Primitive polynomial
In field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite extension field GF...
over the integers mod 2. Values of j and k satisfying this constraint have been published in the literature. Popular pairs are:
- {j = 7, k = 10}, {j = 5, k = 17}, {j = 24, k = 55}, {j = 65, k = 71}, {j = 128, k = 159} http://www.ccs.uky.edu/csep/RN/RN.html, {j = 6, k = 31}, {j = 31, k = 63}, {j = 97, k = 127}, {j = 353, k = 521}, {j = 168, k = 521}, {j = 334, k = 607}, {j = 273, k = 607}, {j = 418, k = 1279} http://www.nersc.gov/nusers/resources/software/libs/math/random/www2.0/DOCS/www/parameters.html
Another list of possible values for j and k is on page 29 of volume 2 of The Art of Computer Programming
The Art of Computer Programming
The Art of Computer Programming is a comprehensive monograph written by Donald Knuth that covers many kinds of programming algorithms and their analysis....
:
, (38,89), (37,100), (30,127), (83,258), (107,378), (273,607), (1029,2281), (576,3217), (4187,9689), (7083,19937), (9739,23209)
Note that the smaller number have short periods (only a few "random" numbers are generated before the first "random" number is repeated and the sequence restarts).
It is required that at least one of the first k values chosen to initialise the generator be odd.
It has been suggested that good ratios between j and k are approximately the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
.
Problems with LFGs
In a paper on four-tap shift registers, Robert M. Ziff states that "It is now widely known that such generators, in particular with the two-tap rules such as R(103, 250), have serious deficiencies. MarsagliaGeorge Marsaglia
George Marsaglia was an American mathematician and computer scientist. He established the lattice structure of congruential random number generators in the paper "Random numbers fall mainly in the planes". This phenomenon is sometimes called the Marsaglia effect...
observed very poor behavior with R(24,55) and smaller generators, and advised against using generators of this type altogether. ... The basic problem of two-tap generators R(a, b) is that they have a built-in three-point correlation between
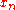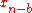, , and , simply given by the generator itself ... While these correlations are spread over the size of the generator itself, they can evidently still lead to significant errors.".The initialization of LFGs is a very complex problem. The output of LFGs is very sensitive to initial conditions, and statistical defects may appear initially but also periodically in the output sequence unless extreme care is taken . Another potential problem with LFGs is that the mathematical theory behind them is incomplete, making it necessary to rely on statistical tests rather than theoretical performance.
Usage
- FreecivFreecivFreeciv is a multiplayer , turn-based strategy game for workstations and personal computers inspired by the commercial proprietary Sid Meier's Civilization series...
uses a lagged Fibonacci generator with {j = 24, k = 55} for its random number generator. - The Boost libraryBoost libraryBoost is a set of free software libraries that extend the functionality of C++.-Overview:Most of the Boost libraries are licensed under the Boost Software License, designed to allow Boost to be used with both free and proprietary software projects...
includes an implementation of a lagged Fibonacci generator. - The Oracle DatabaseOracle DatabaseThe Oracle Database is an object-relational database management system produced and marketed by Oracle Corporation....
implements this generator in its DBMS_RANDOM package (available in Oracle 8 and newer versions).
See also
- Linear congruential generatorLinear congruential generatorA Linear Congruential Generator represents one of the oldest and best-known pseudorandom number generator algorithms. The theory behind them is easy to understand, and they are easily implemented and fast....
- Mersenne twister
- FISH (cipher)FISH (cipher)The FISH stream cipher is a fast software based stream cipher using Lagged Fibonacci generators, plus a concept from the shrinking generator cipher. It was published by Siemens in 1993. FISH is quite fast in software and has a huge key length...
- Pike
- VIC cipherVIC cipherThe VIC cipher was a pencil and paper cipher used by the Soviet spy Reino Häyhänen, codenamed "VICTOR".It was arguably the most complex hand-operated cipher ever seen, when it was first discovered...