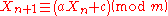
Linear congruential generator
Encyclopedia
A Linear Congruential Generator (LCG) represents one of the oldest and best-known pseudorandom number generator
algorithm
s. The theory behind them is easy to understand, and they are easily implemented and fast.
The generator is defined by the recurrence relation
:
where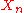
is the sequence
of pseudorandom values, and
are integer
constants that specify the generator. If c = 0, the generator is often called a multiplicative congruential method, or Lehmer RNG. If c ≠ 0, the generator is called a mixed congruential method.
of a general LCG is at most m, and for some choices of a much less than that. Provided that c is nonzero, the LCG will have a full period for all seed values if and only if
:
While LCGs are capable of producing decent pseudorandom numbers, this is extremely sensitive to the choice of the parameters c, m, and a.
Historically, poor choices had led to ineffective implementations of LCGs. A particularly illustrative example of this is RANDU which was widely used in the early 1970s and lead to many results which are currently being questioned because of the use of this poor LCG.
of various compiler
s.
As shown above, LCG's do not always use all of the bits in the values they produce. The Java implementation produces 48 bits with each iteration but only returns the 32 most significant bits from these values. This is because the higher-order bits have longer periods than the lower order bits (see below). LCG's that use this technique produce much better values than those that do not.
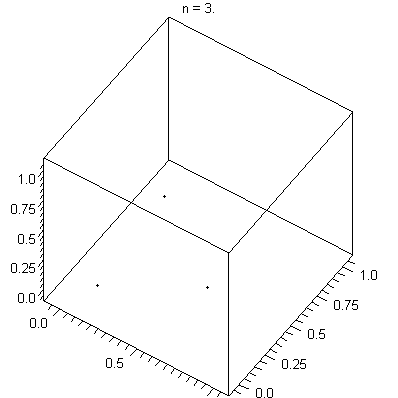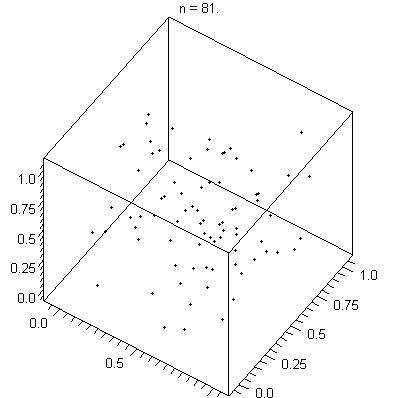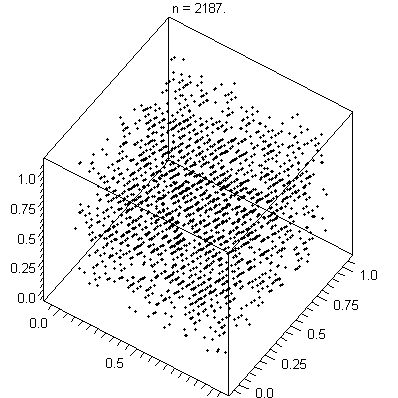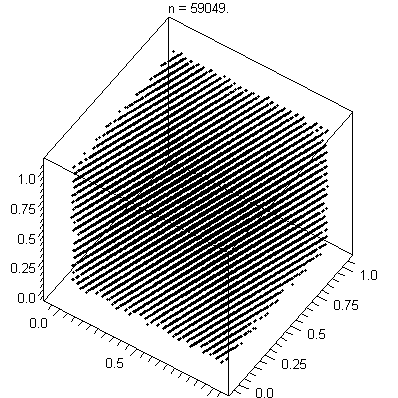LCGs should not be used for applications where high-quality randomness
is critical. For example, it is not suitable for a Monte Carlo simulation because of the serial correlation
(among other things). They should also not be used for cryptographic applications; see cryptographically secure pseudo-random number generator for more suitable generators. If a linear congruential generator is seeded with a character and then iterated once, the result is a simple classical cipher called an affine cipher
; this cipher is easily broken by standard frequency analysis
.
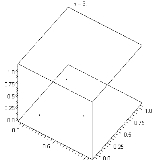
LCGs tend to exhibit some severe defects. For instance, if an LCG is used to choose points in an n-dimensional space, the points will lie on, at most, m1/n hyperplanes (Marsaglia's Theorem, developed by George Marsaglia
). This is due to serial correlation between successive values of the sequence Xn. The spectral test, which is a simple test of an LCG's quality, is based on this fact.
A further problem of LCGs is that the lower-order bits of the generated sequence have a far shorter period than the sequence as a whole if m is set to a power of 2
. In general, the nth least significant digit in the base b representation of the output sequence, where bk = m for some integer k, repeats with at most period bn.
Nevertheless, LCGs may be a good option. For instance, in an embedded system, the amount of memory available is often severely limited. Similarly, in an environment such as a video game console
taking a small number of high-order bits of an LCG may well suffice. The low-order bits of LCGs when m is a power of 2 should never be relied on for any degree of randomness whatsoever. Indeed, simply substituting 2n for the modulus term reveals that the low order bits go through very short cycles. In particular, any full-cycle LCG when m is a power of 2 will produce alternately odd and even results.
s), then the Mersenne twister algorithm provides a vastly longer period (219937-1) and variate uniformity. The Mersenne twister generates higher-quality deviates than almost any LCG. A common Mersenne twister implementation, interestingly enough, uses an LCG to generate seed data.
A Linear Feedback Shift Register
PRNG can be implemented with essentially the same amount of memory and produces a stream of pseudorandom numbers with better randomness qualities when considering streams of bits, albeit with a bit more computation.
Pseudorandom number generator
A pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s. The theory behind them is easy to understand, and they are easily implemented and fast.
The generator is defined by the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
:
where
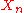is the sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of pseudorandom values, and
-
— the "modulusModulo operationIn computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
" -
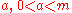— the "multiplier" -
— the "increment" -
— the "seed" or "start value"
are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
constants that specify the generator. If c = 0, the generator is often called a multiplicative congruential method, or Lehmer RNG. If c ≠ 0, the generator is called a mixed congruential method.
Period length
The periodPeriodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
of a general LCG is at most m, and for some choices of a much less than that. Provided that c is nonzero, the LCG will have a full period for all seed values if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
:
-
and 
are relatively prime, -
is divisible by all prime factorPrime factorIn number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s of
, -
is a multiple of 4 if 
is a multiple of 4.
While LCGs are capable of producing decent pseudorandom numbers, this is extremely sensitive to the choice of the parameters c, m, and a.
Historically, poor choices had led to ineffective implementations of LCGs. A particularly illustrative example of this is RANDU which was widely used in the early 1970s and lead to many results which are currently being questioned because of the use of this poor LCG.
Parameters in common use
The most efficient LCGs have an m equal to a power of 2, most often m = 232 or m = 264, because this allows the modulus operation to be computed by merely truncating all but the rightmost 32 or 64 bits. The following table lists the parameters of LCGs in common use, including built-in rand functions in runtime librariesRuntime library
In computer programming, a runtime library is a special program library used by a compiler, to implement functions built into a programming language, during the execution of a computer program...
of various compiler
Compiler
A compiler is a computer program that transforms source code written in a programming language into another computer language...
s.
| Source | m | a | c | output bits of seed in rand / Random(L) |
|---|---|---|---|---|
| Numerical Recipes Numerical Recipes Numerical Recipes is the generic title of a series of books on algorithms and numerical analysis by William H. Press, Saul Teukolsky, William Vetterling and Brian Flannery. In various editions, the books have been in print since 1986... |
232 | 1664525 | 1013904223 | |
| Borland Borland Borland Software Corporation is a software company first headquartered in Scotts Valley, California, Cupertino, California and finally Austin, Texas. It is now a Micro Focus subsidiary. It was founded in 1983 by Niels Jensen, Ole Henriksen, Mogens Glad and Philippe Kahn.-The 1980s:... C/C++ |
232 | 22695477 | 1 | bits 30..16 in rand, 30..0 in lrand |
| glibc (used by GCC GNU Compiler Collection The GNU Compiler Collection is a compiler system produced by the GNU Project supporting various programming languages. GCC is a key component of the GNU toolchain... ) |
232 | 1103515245 | 12345 | bits 30..0 |
| ANSI C ANSI C ANSI C refers to the family of successive standards published by the American National Standards Institute for the C programming language. Software developers writing in C are encouraged to conform to the standards, as doing so aids portability between compilers.-History and outlook:The first... : Watcom Watcom C compiler The Watcom C/C++ compiler is a compiler for the computer programming languages C and C++ that produces executable programs for several platforms and operating systems. The code it produces for MS-DOS executes very fast. It was one of the first compilers to support the Intel 80386 "protected mode"... , Digital Mars Digital Mars Digital Mars is a small American software company owned by Walter Bright that makes C and C++ compilers for Windows and DOS. They also distribute the compilers for free on their web site.... , CodeWarrior CodeWarrior CodeWarrior is an integrated development environment for the creation of software that runs on a number of embedded systems. Prior to the acquisition of the product by Freescale Semiconductor, versions existed for Macintosh, Microsoft Windows, Linux, Solaris, PlayStation 2, Nintendo GameCube,... , IBM VisualAge C/C++ |
232 | 1103515245 | 12345 | bits 30..16 |
| Borland Delphi Borland Delphi Embarcadero Delphi is an integrated development environment for console, desktop graphical, web, and mobile applications.Delphi's compilers use its own Object Pascal dialect of Pascal and generate native code for 32- and 64-bit Windows operating systems, as well as 32-bit Mac OS X and iOS... , Virtual Pascal Virtual Pascal Virtual Pascal is a free 32-bit Pascal compiler, IDE, and debugger for OS/2 and Microsoft Windows, with some limited Linux support. Although it had a wide user base in the late 1990s, VP has not evolved significantly for several years, and the owner declared in 2005 that development had ceased... |
232 | 134775813 | 1 | bits 63..32 of (seed * L) |
| Microsoft Visual/Quick C/C++ Visual C++ Microsoft Visual C++ is a commercial , integrated development environment product from Microsoft for the C, C++, and C++/CLI programming languages... |
232 | 214013 | 2531011 | bits 30..16 |
| Microsoft Visual Basic Visual Basic Visual Basic is the third-generation event-driven programming language and integrated development environment from Microsoft for its COM programming model... (6 and earlier) |
224 | 1140671485 | 12820163 | |
| RtlUniform from Native API Native API The Native API is the publicly- and incompletely-documented application programming interface used internally by the Windows NT family of operating systems produced by Microsoft.. It is predominately used during system boot, when other components of Windows are unavailable. The Program Entry point... |
231 − 1 | 2147483629 | 2147483587 | |
| Apple CarbonLib | 231 − 1 | 16807 | 0 | see MINSTD |
| MMIX MMIX MMIX is a 64-bit RISC instruction set architecture designed by Donald Knuth, with significant contributions by John L. Hennessy and Richard L. Sites... by Donald Knuth Donald Knuth Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms... |
264 | 6364136223846793005 | 1442695040888963407 | |
| VAX VAX VAX was an instruction set architecture developed by Digital Equipment Corporation in the mid-1970s. A 32-bit complex instruction set computer ISA, it was designed to extend or replace DEC's various Programmed Data Processor ISAs... 's MTH$RANDOM, old versions of glibc |
232 | 69069 | 1 | |
| Java Java (programming language) Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities... 's java.util.Random |
248 | 25214903917 | 11 | bits 47...16 |
| LC53 in Forth (programming language) | 232 − 5 | 232 − 333333333 | 0 | |
As shown above, LCG's do not always use all of the bits in the values they produce. The Java implementation produces 48 bits with each iteration but only returns the 32 most significant bits from these values. This is because the higher-order bits have longer periods than the lower order bits (see below). LCG's that use this technique produce much better values than those that do not.
Advantages and disadvantages of LCGs
LCGs are fast and require minimal memory (typically 32 or 64 bits) to retain state. This makes them valuable for simulating multiple independent streams.Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
is critical. For example, it is not suitable for a Monte Carlo simulation because of the serial correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
(among other things). They should also not be used for cryptographic applications; see cryptographically secure pseudo-random number generator for more suitable generators. If a linear congruential generator is seeded with a character and then iterated once, the result is a simple classical cipher called an affine cipher
Affine cipher
The affine cipher is a type of monoalphabetic substitution cipher, wherein each letter in an alphabet is mapped to its numeric equivalent, encrypted using a simple mathematical function, and converted back to a letter...
; this cipher is easily broken by standard frequency analysis
Frequency analysis
In cryptanalysis, frequency analysis is the study of the frequency of letters or groups of letters in a ciphertext. The method is used as an aid to breaking classical ciphers....
.
LCGs tend to exhibit some severe defects. For instance, if an LCG is used to choose points in an n-dimensional space, the points will lie on, at most, m1/n hyperplanes (Marsaglia's Theorem, developed by George Marsaglia
George Marsaglia
George Marsaglia was an American mathematician and computer scientist. He established the lattice structure of congruential random number generators in the paper "Random numbers fall mainly in the planes". This phenomenon is sometimes called the Marsaglia effect...
). This is due to serial correlation between successive values of the sequence Xn. The spectral test, which is a simple test of an LCG's quality, is based on this fact.
A further problem of LCGs is that the lower-order bits of the generated sequence have a far shorter period than the sequence as a whole if m is set to a power of 2
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
. In general, the nth least significant digit in the base b representation of the output sequence, where bk = m for some integer k, repeats with at most period bn.
Nevertheless, LCGs may be a good option. For instance, in an embedded system, the amount of memory available is often severely limited. Similarly, in an environment such as a video game console
Video game console
A video game console is an interactive entertainment computer or customized computer system that produces a video display signal which can be used with a display device to display a video game...
taking a small number of high-order bits of an LCG may well suffice. The low-order bits of LCGs when m is a power of 2 should never be relied on for any degree of randomness whatsoever. Indeed, simply substituting 2n for the modulus term reveals that the low order bits go through very short cycles. In particular, any full-cycle LCG when m is a power of 2 will produce alternately odd and even results.
Comparison with other PRNGs
If higher quality random numbers are needed, and sufficient memory is available (~ 2 kilobyteKilobyte
The kilobyte is a multiple of the unit byte for digital information. Although the prefix kilo- means 1000, the term kilobyte and symbol KB have historically been used to refer to either 1024 bytes or 1000 bytes, dependent upon context, in the fields of computer science and information...
s), then the Mersenne twister algorithm provides a vastly longer period (219937-1) and variate uniformity. The Mersenne twister generates higher-quality deviates than almost any LCG. A common Mersenne twister implementation, interestingly enough, uses an LCG to generate seed data.
A Linear Feedback Shift Register
Linear feedback shift register
A linear feedback shift register is a shift register whose input bit is a linear function of its previous state.The most commonly used linear function of single bits is XOR...
PRNG can be implemented with essentially the same amount of memory and produces a stream of pseudorandom numbers with better randomness qualities when considering streams of bits, albeit with a bit more computation.
See also
- Full cycleFull CycleA full cycle is a mathematical term that represents a traversal over a set of non-random numbers. A full cycle implies that every number in the set was chosen exactly once before repeating.Full cycles are useful in Pseudorandom number generators....
- Inversive congruential generatorInversive congruential generatorInversive congruential generators are a type of nonlinear congruential pseudorandom number generator, which use the modular multiplicative inverse to generate the next number in a sequence...
- Multiply-with-carryMultiply-with-carryIn computer science, multiply-with-carry is a method invented by George Marsaglia for generating sequences of random integers based on an initial set of from two to many thousands of randomly chosen seed values...
- Lehmer RNG (sometimes called the Park-Miller RNG)
External links
- The simulation Linear Congruential Generator visualizes the correlations between the pseudo-random numbers when manipulating the parameters.
- Security of Random Number Generation: An Annotated Bibliography
- Linear Congruential Generators post to sci.math
- The "Death of Art" computer art project at Goldstein Technologies LLC, uses an LCG to generate 33,554,432 images
- P. L'Ecuyer and R. Simard, ``TestU01: A C Library for Empirical Testing of Random Number Generators, May 2006, Revised November 2006, ACM Transactions on Mathematical Software, 33, 4, Article 22, August 2007.
- Additive Congruential Method : maths and logic behind its spread