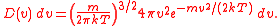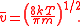Maxwell Speed Distribution
Encyclopedia
Classically, an ideal gas
' molecule
s bounce around with somewhat arbitrary velocities, never interacting with each other. In reality, however, an ideal gas is subjected to intermolecular force
s. It is to be noted that the aforementioned classical treatment of an ideal gas is only useful when modeling situations in which the particle density is very low. In such situations, the particles themselves can be considered to have approximately zero volume when compared to the volume which contains them, thus giving rise to classical theory. i.e. given that such a situation would have an extremely low probability of having molecules interact with each other.
Consequently, we need to consider these interactions in order to acquire a more accurate sense of how particles behave in a gas. This leads us to Maxwell's speed distribution (MSD), named after James Clerk Maxwell
to whom this theory is attributed. MSD is a probability distribution describing the dispersion of these molecular speeds. MSD can only be applied when dealing with an ideal gas. More accurately, we apply MSD to gases that are "almost" ideal, given that no gas is truly ideal. Air, for example, at STP behaves similarly to an ideal gas, allowing MSD to be applied.
Note that speed
is a scalar quantity, describing how fast the particles are moving, regardless of direction. Velocity
, on the other hand, describes the direction as well as the speed at which the particles are moving. This is a necessary consideration given that space is three dimensional, implying that for any given speed, there are many possible velocity vectors.
The probability of a molecule having a given speed can be found by using the Boltzmann factor
. Considering the energy to be dependent only on the kinetic energy, we find that:
where, m is the mass of the molecule, k is Boltzmann's constant, and T is the temperature.
The above equation gives us the probability of a given speed component, which we can assume to be any of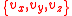
without loss of generality. In 3 dimensions, we need to consider that particles can have all possible combinations of 
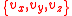speed components, which leads us to the need to consider 
, as opposed to just considering v. In other words, we need to sum all potential combinations of the individual components in 3 dimensional velocity space in order for their vector sum to be the desired value. To get the distribution in 3 dimensions, we need to integrate the above equations in 
over the entire velocity space such that the component sum is constant. If we picture the particles with speed v in a 3-dimensional velocity space, we can see that these particles lie on the surface of a sphere with radius v. The larger v is, the bigger the sphere, and the more possible velocity vectors there are. So the number of possible velocity vectors for a given speed is analogous to the surface area of a sphere of radius v.
Multiplying these two functions together gives us the distribution, and normalising this gives us the MSD in its entirety.
(Again, m is the mass of the molecule, k is Boltzmann's constant, and T is the temperature.)
Since this formula is a normalised probability distribution
, it gives the probability of a molecule having a speed between
and v + dv. The probability of a molecule having a speed between two different values v0 and v1 can be found by integrating this function with v0 and v1 as the bounds.
Firstly, by finding the maximum of the MSD (by differentiating, setting the derivative equal to zero and solving for the speed), we can determine the most probable speed. Calling this vmp, we find that:
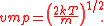
Second, we can find the root mean square
of the speed by finding the expected value
of v2. (Alternatively, and much simpler, we can solve it by using the equipartition theorem
.) Calling this vrms:
Third and finally, we can find the mean value of v from the MSD. Calling this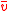
:
Notice that
These are three different ways of defining the average velocity, and they are not numerically the same. It is important to be clear about which quantity is being used.
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
' molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s bounce around with somewhat arbitrary velocities, never interacting with each other. In reality, however, an ideal gas is subjected to intermolecular force
Intermolecular force
Intermolecular forces are forces of attraction or repulsion which act between neighboring particles: atoms, molecules or ions. They are weak compared to the intramolecular forces, the forces which keep a molecule together...
s. It is to be noted that the aforementioned classical treatment of an ideal gas is only useful when modeling situations in which the particle density is very low. In such situations, the particles themselves can be considered to have approximately zero volume when compared to the volume which contains them, thus giving rise to classical theory. i.e. given that such a situation would have an extremely low probability of having molecules interact with each other.
Consequently, we need to consider these interactions in order to acquire a more accurate sense of how particles behave in a gas. This leads us to Maxwell's speed distribution (MSD), named after James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
to whom this theory is attributed. MSD is a probability distribution describing the dispersion of these molecular speeds. MSD can only be applied when dealing with an ideal gas. More accurately, we apply MSD to gases that are "almost" ideal, given that no gas is truly ideal. Air, for example, at STP behaves similarly to an ideal gas, allowing MSD to be applied.
Note that speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
is a scalar quantity, describing how fast the particles are moving, regardless of direction. Velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, on the other hand, describes the direction as well as the speed at which the particles are moving. This is a necessary consideration given that space is three dimensional, implying that for any given speed, there are many possible velocity vectors.
The probability of a molecule having a given speed can be found by using the Boltzmann factor
Boltzmann factor
In physics, the Boltzmann factor is a weighting factor that determines the relative probability of a particle to be in a state i in a multi-state system in thermodynamic equilibrium at temperature T...
. Considering the energy to be dependent only on the kinetic energy, we find that:
where, m is the mass of the molecule, k is Boltzmann's constant, and T is the temperature.
The above equation gives us the probability of a given speed component, which we can assume to be any of
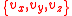without loss of generality. In 3 dimensions, we need to consider that particles can have all possible combinations of 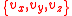speed components, which leads us to the need to consider , as opposed to just considering v. In other words, we need to sum all potential combinations of the individual components in 3 dimensional velocity space in order for their vector sum to be the desired value. To get the distribution in 3 dimensions, we need to integrate the above equations in over the entire velocity space such that the component sum is constant. If we picture the particles with speed v in a 3-dimensional velocity space, we can see that these particles lie on the surface of a sphere with radius v. The larger v is, the bigger the sphere, and the more possible velocity vectors there are. So the number of possible velocity vectors for a given speed is analogous to the surface area of a sphere of radius v.
Multiplying these two functions together gives us the distribution, and normalising this gives us the MSD in its entirety.
(Again, m is the mass of the molecule, k is Boltzmann's constant, and T is the temperature.)
Since this formula is a normalised probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, it gives the probability of a molecule having a speed between
and v + dv. The probability of a molecule having a speed between two different values v0 and v1 can be found by integrating this function with v0 and v1 as the bounds.Averages
There are three candidates for what is called the "average" value of the speed of the Maxwell speed distribution.Firstly, by finding the maximum of the MSD (by differentiating, setting the derivative equal to zero and solving for the speed), we can determine the most probable speed. Calling this vmp, we find that:
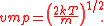
Second, we can find the root mean square
Root mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
of the speed by finding the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of v2. (Alternatively, and much simpler, we can solve it by using the equipartition theorem
Equipartition theorem
In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition...
.) Calling this vrms:
Third and finally, we can find the mean value of v from the MSD. Calling this
:
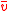Notice that
These are three different ways of defining the average velocity, and they are not numerically the same. It is important to be clear about which quantity is being used.
See also
- Boltzmann distributionBoltzmann distributionIn chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
- Maxwell-Boltzmann distribution