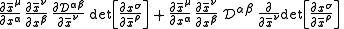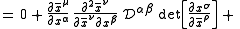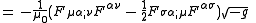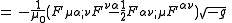Maxwell's equations in curved spacetime
Encyclopedia
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
in curved
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
(where the metric
Metric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
may not be the Minkowski metric) or where one uses an arbitrary (not necessarily Cartesian
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
) coordinate system. These equations can be viewed as a generalization of the vacuum Maxwell's equations which are normally formulated in the local coordinates
Local coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
of flat spacetime. But because general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
dictates that the presence of electromagnetic fields (or energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
/matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
in general) induce curvature in spacetime, Maxwell's equations in flat spacetime should be viewed as a convenient approximation.
When working in the presence of bulk matter, it is preferable to distinguish between free and bound electric charges. Without that distinction, the vacuum Maxwell's equations are called the "microscopic" Maxwell's equations. When the distinction is made, they are called the macroscopic Maxwell's equations.
The reader is assumed to be familiar with the four dimensional form of electromagnetism in flat space-time and basic mathematics of curved spacetime.
The electromagnetic field also admits a coordinate-independent geometric description, and Maxwell's equations expressed in terms of these geometric objects are the same in any spacetime, curved or not. Also, the same modifications are made to the equations of flat Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
when using local coordinates that are not Cartesian. For example, the equations in this article can be used to write Maxwell's equations in spherical coordinates. For these reasons, it may be useful to think of Maxwell's equations in Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
as a special case
Special case
In logic, especially as applied in mathematics, concept A is a special case or specialization of concept B precisely if every instance of A is also an instance of B, or equivalently, B is a generalization of A. For example, all circles are ellipses ; therefore the circle is a special case of the...
, rather than Maxwell's equations in curved spacetimes as a generalization.
Summary
In general relativity, the equations of electromagnetism in a vacuum become:

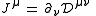
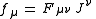
where fμ is the density of Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
, gαβ is the reciprocal of the metric tensor
Metric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
gαβ, and g is the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the metric tensor. Notice that Aα and Fαβ are (ordinary) tensors while
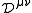 , Jμ, and fμ are tensor densities
, Jμ, and fμ are tensor densitiesTensor density
In differential geometry, a tensor density or relative tensor is a generalization of the tensor concept. A tensor density transforms as a tensor when passing from one coordinate system to another , except that it is additionally multiplied or weighted by a power of the Jacobian determinant of the...
of weight +1. Despite the use of partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s, these equations are invariant under arbitrary curvilinear coordinate transformations. Thus if one replaced the partial derivatives with covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
s, the extra terms thereby introduced would cancel out.
The electromagnetic potential
The electromagnetic potentialElectromagnetic four-potential
The electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...
is a covariant vector,
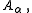 which is the undefined primitive of electromagnetism. As a covariant vector, its rule for transforming from one coordinate system to another is
which is the undefined primitive of electromagnetism. As a covariant vector, its rule for transforming from one coordinate system to another is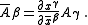
Electromagnetic field
The electromagnetic fieldElectromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
is a covariant antisymmetric rank 2 tensor which can be defined in terms of the electromagnetic potential by

To see that this equation is invariant, we transform the coordinates (as described in the classical treatment of tensors)





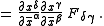
This definition implies that the electromagnetic field satisfies

which incorporates Faraday's law of induction
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
and Gauss's law for magnetism. This is seen by


Although there appear to be 64 equations in Faraday-Gauss, it actually reduces to just four independent equations. Using the antisymmetry of the electromagnetic field one can either reduce to an identity (0=0) or render redundant all the equations except for those with λ,μ,ν = either 1,2,3 or 2,3,0 or 3,0,1 or 0,1,2.
The Faraday-Gauss equation is sometimes written


where the semicolon indicates a covariant derivative, comma indicate a partial derivative, and square brackets indicate anti-symmetrization. The covariant derivative of the electromagnetic field is
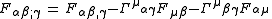
where Γαβ γ is the Christoffel symbol which is symmetric in its lower indices.
Electromagnetic displacement
The electric displacement field,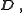 and the auxiliary magnetic field,
and the auxiliary magnetic field, 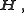 form an antisymmetric contravariant rank 2 tensor density of weight +1. In a vacuum, this is given by
form an antisymmetric contravariant rank 2 tensor density of weight +1. In a vacuum, this is given by
Notice that this equation is the only place where the metric (and thus gravity) enters into the theory of electromagnetism. Furthermore even here, the equation is invariant under a change of scale, that is, multiplying the metric by a constant has no effect on this equation. Consequently, gravity can only affect electromagnetism by changing the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
relative to the global coordinate system being used. Light is only deflected by gravity because it is slower when near to massive bodies. So it is as if gravity increased the index of refraction of space near massive bodies.
More generally, in materials where the magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
-polarization tensor is non-zero, we have
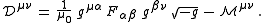
The transformation law for electromagnetic displacement is

where the Jacobian determinant is used. If the magnetization-polarization tensor is used, it has the same transformation law as the electromagnetic displacement.
Electric current
The electric current is the divergence of the electromagnetic displacement. In a vacuum,
If magnetization-polarization is used, then this just gives the free portion of the current
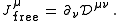
This incorporates Ampere's Law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
and Gauss's Law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
.
In either case, the fact that the electromagnetic displacement is antisymmetric implies that the electric current is automatically conserved
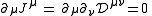
because the partial derivatives commute.
The Ampere-Gauss definition of the electric current is not sufficient to determine its value because the electromagnetic potential (from which is was ultimately derived) has not been given a value. Instead, the usual procedure is to equate the electric current to some expression in terms of other fields, mainly the electron and proton, and then solve for the electromagnetic displacement, electromagnetic field, and electromagnetic potential.
The electric current is a contravariant vector density, and as such it transforms as follows

Verification of this transformation law

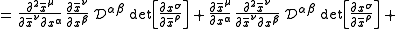
So all that remains is to show that

which is a version of a known theorem (see Inverse functions and differentiation#Higher derivatives).
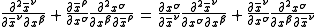


Lorentz force
The density of the Lorentz forceLorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
is a covariant vector density given by

The force on a test particle subject only to gravity and electromagnetism is

where p is the linear 4-momentum of the particle, t is any time coordinate parameterizing the world line of the particle, Γ is the Christoffel symbol (gravitational force field), and q is the electric charge of the particle.
This equation is invariant under a change in the time coordinate; just multiply by
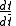 and use the chain rule
and use the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
. It is also invariant under a change in the x coordinate system.
Using the transformation law for the Christoffel symbol

we get

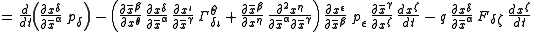
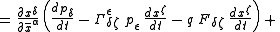
-
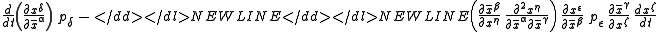
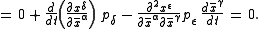
Lagrangian
In a vacuum, the LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
for classical electrodynamics (in joules/meter3) is a scalar densityTensor densityIn differential geometry, a tensor density or relative tensor is a generalization of the tensor concept. A tensor density transforms as a tensor when passing from one coordinate system to another , except that it is additionally multiplied or weighted by a power of the Jacobian determinant of the...
where The four-current should be understood as an abbreviation of many terms expressing the electric currents of other charged fields in terms of their variables.
The four-current should be understood as an abbreviation of many terms expressing the electric currents of other charged fields in terms of their variables.
If we separate free currents from bound currents, the Lagrangian becomes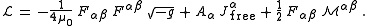
Electromagnetic stress-energy tensor
As part of the source term in the Einstein field equationsEinstein field equationsThe Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
, the electromagnetic stress-energy tensorStress-energy tensorThe stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
is a covariant symmmetric tensor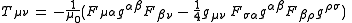
which is trace-free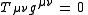
because electromagnetism propagates at the invariant speedInvariant speedThe invariant speed or observer invariant speed is the speed an object or particle must be traveling at for its speed to have the same measure in all reference frames. The invariance of the speed of light is a consequence of the postulates of special relativity, and the terms speed of light and...
.
In the expression for the conservation of energy and linear momentum, the electromagnetic stress-energy tensor is best represented as a mixed tensor density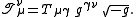
From the equations above, one can show that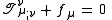
where the semicolon indicates a covariant derivativeCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
.
This can be rewritten as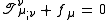
which says that the decrease in the electromagnetic energy is the same as the work done by the electromagnetic field on the gravitational field plus the work done on matter (via the Lorentz force), and similarly the rate of decrease in the electromagnetic linear momentum is the electromagnetic force exerted on the gravitational field plus the Lorentz force exerted on matter.
Derivation of conservation law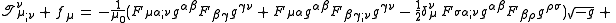
which is zero because it is the negative of itself (see four lines above).
Electromagnetic wave equation
The nonhomogeneous electromagnetic wave equation in terms of the field tensor is modified from the special relativity formFormulation of Maxwell's equations in special relativityThe covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form which is "manifestly covariant" , in the formalism of special relativity...
to

where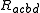 is the covariant form of the Riemann tensor and
is the covariant form of the Riemann tensor and 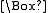 is a generalization of the d'Alembertian operator for covariant derivatives. Using
is a generalization of the d'Alembertian operator for covariant derivatives. Using

Maxwell's source equations can be written in terms of the 4-potential [ref 2, p. 569] as,
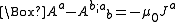
or, assuming the generalization of the Lorenz gauge in curved spacetime ,
,
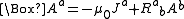
where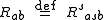 is the Ricci curvature tensor.
is the Ricci curvature tensor.
This the same form of the wave equation as in flat spacetime, except that the derivatives are replaced by covariant derivatives and there is an additional term proportional to the curvature. The wave equation in this form also bears some resemblance to the Lorentz force in curved spacetime where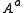 plays the role of the 4-position.
plays the role of the 4-position.
Nonlinearity of Maxwell's equations in a dynamic spacetime
When Maxwell's equations are treated in a background independent manner, that is, when the spacetime metric is taken to be a dynamical variable dependent on the electromagnetic field, then the electromagnetic wave equation and Maxwell's equations are nonlinear. This can be seen by noting that the curvature tensor depends on the stress-energy tensor through the Einstein field equation

where
is the Einstein tensorEinstein tensorIn differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
,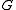 is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, is the metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
is the metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
, and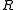 (scalar curvatureScalar curvatureIn Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
(scalar curvatureScalar curvatureIn Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
) is the trace of the Ricci curvature tensor. The stress-energy tensor is composed of the stress-energy from particles, but also stress-energy from the electromagnetic field. This generates the nonlinearity.
Geometric formulation
The geometric view of the electromagnetic field is that it is the curvature 2-form of a principal U(1)-bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
, and acts on charged matter by holonomyHolonomyIn differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
. In this view, one of Maxwell's two equations, d F= 0, is a mathematical identity known as the Bianchi identity. This equation implies, by the Poincaré lemma, that there exists (at least locally) a 1-form A satisfying F = d A. The other Maxwell equation is
where the curvature 2-form F is known as the Faraday 2-form in this context, J is the current 3-form, the asterisk * denotes the Hodge star operator, and d is the exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
operator.
The dependence of Maxwell's equation (there is only one with any physical content in this language) on the metric of spacetime lies in the Hodge star operator. Written this way, Maxwell's equation is the same in any spacetime.
See also
- Electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
- Nonhomogeneous electromagnetic wave equation
- Formulation of Maxwell's equations in special relativityFormulation of Maxwell's equations in special relativityThe covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form which is "manifestly covariant" , in the formalism of special relativity...
- Theoretical motivation for general relativityTheoretical motivation for general relativityA Theoretical motivation for general relativity, including the motivation for the geodesic equation and the Einstein field equation, can be obtained from special relativity by examining the dynamics of particles in circular orbits about the earth. A key advantage in examining circular orbits is...
- Basic introduction to the mathematics of curved spacetimeBasic introduction to the mathematics of curved spacetimeThe mathematics of general relativity are very complex. In Newton's theories of motions, an object's mass and length remain constant as it changes speed, and the rate of passage of time also remains unchanged. As a result, many problems in Newtonian mechanics can be solved with algebra alone...
- Electrovacuum solutionElectrovacuum solutionIn general relativity, an electrovacuum solution is an exact solution of the Einstein field equation in which the only nongravitational mass-energy present is the field energy of an electromagnetic field, which must satisfy the source-free Maxwell equations appropriate to the given geometry...
External links
-