
Matrix function
Encyclopedia
In mathematics
, a matrix function is a function
which maps a matrix
to another matrix.
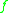 has the Taylor expansion
has the Taylor expansion
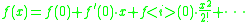
then a matrix function can be defined by substituting by a matrix: the powers become matrix powers, the additions become matrix sums and the multiplications become scaling operations. If the real series converges for
by a matrix: the powers become matrix powers, the additions become matrix sums and the multiplications become scaling operations. If the real series converges for 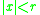 , then the corresponding matrix series will converge for matrix argument A if
, then the corresponding matrix series will converge for matrix argument A if  for some matrix norm
for some matrix norm  which satisfies
which satisfies 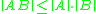 .
.
,
then we can find a matrix P and a diagonal matrix
D
such that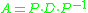 .
.
Applying the power series definition to this decomposition, we find that is defined by
is defined by
where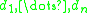 denote the diagonal entries of D.
denote the diagonal entries of D.
All matrices, whether they are diagonalizable or not,
have a Jordan normal form
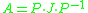 ,
,
where the matrix J consists of Jordan blocks.
Consider these blocks separately and apply the power series to a Jordan block: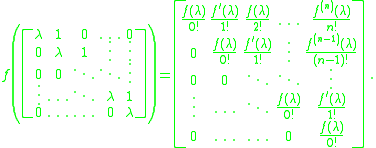
This definition can be used to extend the domain of the matrix function
beyond the set of matrices with spectral radius smaller than the radius of convergence of the power series.
Note that there is also a connection to divided differences.
A related notion is the Jordan–Chevalley decomposition which expresses a matrix as a sum of a diagonalizable and a nilpotent part.
from complex analysis
can also be used to generalize scalar functions to matrix functions. Cauchy's integral formula states that for any analytic function
f defined on a set D⊂ℂ, it holds
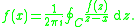 ,
,
where C is a closed curve inside the domain D enclosing x. Now replace x by a matrix A and consider a path C inside D that encloses all eigenvalues of A. One possibility to achieve this is to let C be a circle around the origin
with radius
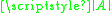 for an arbitrary matrix norm
for an arbitrary matrix norm 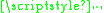 . Then,
. Then, 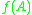 is defined by
is defined by
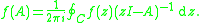
This integral can readily be evaluated numerically using the trapezium rule, which converges exponentially in this case. That means that the precision
of the result doubles when the number of nodes is doubled.
This idea applied to bounded linear operators on a Banach space
, which can be seen as infinite matrices, leads to the holomorphic functional calculus
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a matrix function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which maps a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
to another matrix.
Extending scalar functions to matrix functions
There are several techniques for lifting a real function to a square matrix function such that interesting properties are maintained. All of the following techniques yield the same matrix function, but the domains on which the function are defined may differ.Power series
If the real function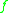 has the Taylor expansion
has the Taylor expansion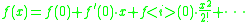
then a matrix function can be defined by substituting
 by a matrix: the powers become matrix powers, the additions become matrix sums and the multiplications become scaling operations. If the real series converges for
by a matrix: the powers become matrix powers, the additions become matrix sums and the multiplications become scaling operations. If the real series converges for 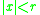 , then the corresponding matrix series will converge for matrix argument A if
, then the corresponding matrix series will converge for matrix argument A if  for some matrix norm
for some matrix norm  which satisfies
which satisfies 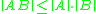 .
.Jordan decomposition
If the matrix A is diagonalizableDiagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
,
then we can find a matrix P and a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
D
such that
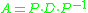 .
.Applying the power series definition to this decomposition, we find that
 is defined by
is defined by
where
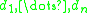 denote the diagonal entries of D.
denote the diagonal entries of D.All matrices, whether they are diagonalizable or not,
have a Jordan normal form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
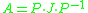 ,
,where the matrix J consists of Jordan blocks.
Consider these blocks separately and apply the power series to a Jordan block:
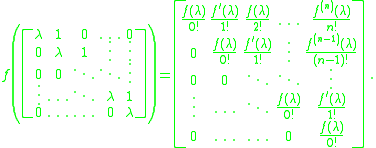
This definition can be used to extend the domain of the matrix function
beyond the set of matrices with spectral radius smaller than the radius of convergence of the power series.
Note that there is also a connection to divided differences.
A related notion is the Jordan–Chevalley decomposition which expresses a matrix as a sum of a diagonalizable and a nilpotent part.
Cauchy integral
Cauchy's integral formulaCauchy's integral formula
In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...
from complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
can also be used to generalize scalar functions to matrix functions. Cauchy's integral formula states that for any analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
f defined on a set D⊂ℂ, it holds
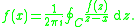 ,
,where C is a closed curve inside the domain D enclosing x. Now replace x by a matrix A and consider a path C inside D that encloses all eigenvalues of A. One possibility to achieve this is to let C be a circle around the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
with radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
 for an arbitrary matrix norm
for an arbitrary matrix norm  . Then,
. Then, 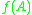 is defined by
is defined by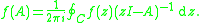
This integral can readily be evaluated numerically using the trapezium rule, which converges exponentially in this case. That means that the precision
Precision (arithmetic)
The precision of a value describes the number of digits that are used to express that value. In a scientific setting this would be the total number of digits or, less commonly, the number of fractional digits or decimal places...
of the result doubles when the number of nodes is doubled.
This idea applied to bounded linear operators on a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, which can be seen as infinite matrices, leads to the holomorphic functional calculus
Holomorphic functional calculus
In mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function ƒ of a complex argument z and an operator T, the aim is to construct an operatorf\,...
.
Examples
- Matrix polynomialCayley–Hamilton theoremIn linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....
- Matrix rootSquare root of a matrixIn mathematics, the square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.-Properties:...
- Matrix logarithm
- Matrix exponentialMatrix exponentialIn mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....

