In numerical analysis

Numerical analysis

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....

, the trapezoidal rule (also known as the trapezoid rule or trapezium rule) is an approximate technique for calculating the definite integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

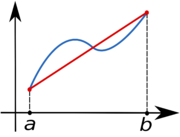
The trapezoidal rule works by approximating the region under the graph of the function
as a trapezoid

Trapezoid

In Euclidean geometry, a convex quadrilateral with one pair of parallel sides is referred to as a trapezoid in American English and as a trapezium in English outside North America. A trapezoid with vertices ABCD is denoted...

 and calculating its area. It follows that

Applicability and alternatives

The trapezoidal rule is one of a family of formulas for numerical integration

Numerical integration

In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...

 called Newton–Cotes formulas, of which the midpoint rule is similar to the trapezoid rule. Simpson's rule

Simpson's rule

In numerical analysis, Simpson's rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:...

 is another member of the same family, and in general has faster convergence than the trapezoidal rule for functions which are twice continuously differentiable, though not in all specific cases. However for various classes of rougher functions (ones with weaker smoothness conditions), the trapezoidal rule has faster convergence in general than Simpson's rule.

Moreover, the trapezoidal rule tends to become extremely accurate when periodic function

Periodic function

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...

s are integrated over their periods, which can be analyzed in various ways.

For non-periodic functions, however, methods with unequally spaced points such as Gaussian quadrature

Gaussian quadrature

In numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration....

 and Clenshaw–Curtis quadrature are generally far more accurate; Clenshaw–Curtis quadrature can be viewed as a change of variables to express arbitrary integrals in terms of periodic integrals, at which point the trapezoidal rule can be applied accurately.

Uniform Grid

For a domain discretized into "N" equally spaced panels, or "N+1" grid points (1, 2, ..., N+1), where the grid spacing is "h=(b-a)/N", the approximation to the integral becomes

Non-uniform Grid

When the grid spacing is non-uniform, one can use the formula

Error analysis

The error of the composite trapezoidal rule is the difference between the value of the integral and the numerical result:


There exists a number ξ between a and b, such that


It follows that if the integrand is concave up (and thus has a positive second derivative), then the error is negative and the trapezoidal rule overestimates the true value. This can also be seen from the geometric picture: the trapezoids include all of the area under the curve and extend over it. Similarly, a concave-down function yields an underestimate because area is unaccounted for under the curve, but none is counted above. If the interval of the integral being approximated includes an inflection point, then the error is harder to identify.

In general, three techniques are used in the analysis of error:

1. Fourier series
   Fourier series
   In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
   
   
2. Residue calculus
3. Euler–Maclaurin summation formula:

An asymptotic error estimate for N → ∞ is given by
Further terms in this error estimate are given by the Euler–Maclaurin summation formula.

It is argued that the speed of convergence of the trapezoidal rule reflects and can be used as a definition of classes of smoothness of the functions.

Periodic functions

The trapezoidal rule often converges very quickly for periodic functions. This can be explained intuitively as:

"When the function is periodic and one integrates over one full period, there are about as many sections of the graph that are concave up as concave down, so the errors cancel."

More detailed analysis can be found in.

"Rough" functions

For various classes of functions that are not twice-differentiable, the trapezoidal rule has sharper bounds than Simpson's rule.

Excel

The trapezoidal rule is easily implemented in Excel

Excel

Excel may refer to:* Microsoft Excel, a spreadsheet application by Microsoft Corporation* Excel , a brand of chewing gum produced by Wrigley's* Excel , a crossover thrash/punk band from Venice, California...

.

As an example, we show the integral of .

Python

The (composite) trapezoidal rule can be implemented in Python

Python (programming language)

Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...

 as follows:

1. !/usr/bin/env python

def trapezoidal_rule(f, a, b, N):
"""Approximate the definite integral of f from a to b by the
composite trapezoidal rule, using N subintervals"""
return (b-a) * ( f(a)/2 + f(b)/2 + sum([f(a + (b-a)*k/N) for k in xrange(1,N)]) ) / N

print trapezoidal_rule(lambda x:x**9, 0.0, 10.0, 100000) # displays 1000000000.75

MATLAB

MATLAB

MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...

 and GNU Octave

GNU Octave

GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB...

The (composite) trapezoidal rule can be implemented in MATLAB

MATLAB

MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...

 as follows:


function [F] = trap(f,a,b,n)

%% f=name of function, a=start value, b=end value, n=number of intervals

h = (b - a) / n;
x = [a:h:b];
for i = 1: length(x)
y(i) = f(x(i));
end
F = h*(y(1) + 2*sum(y(2:end-1)) + y(end))/2;

end


This method is also built-in to MATLAB under the function name trapz.

C++

In C++

C++

C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...

, one can implement the trapezoidal rule as follows.

template
double trapezoid_integrate(const ContainerA &x, const ContainerB &y) {
if (x.size != y.size) {
throw std::logic_error("x and y must be the same size");
}
double sum = 0.0;
for (int i = 1; i < x.size; i++) {
sum += (x[i] - x[i-1]) * (y[i] + y[i-1]);
}
return sum * 0.5;
}

Here, x and y can be any object of a class implementing operator[] and size.

See also

• Rectangle method
  Rectangle method
  In mathematics, specifically in integral calculus, the rectangle method computes an approximation to a definite integral, made by finding the area of a collection of rectangles whose heights are determined by the values of the function.Specifically, the interval over which the function is to be...
  
  
• Simpson's rule
  Simpson's rule
  In numerical analysis, Simpson's rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:...
  
  
• Romberg's method
  Romberg's method
  In numerical analysis, Romberg's method is used to estimate the definite integral \int_a^b f \, dx by applying Richardson extrapolation repeatedly on the trapezium rule or the rectangle rule . The estimates generate a triangular array...
  
  
• Newton–Cotes formulas
• Gaussian quadrature
  Gaussian quadrature
  In numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration....
  
  
• Tai's method
  Tai's method
  Tai's method is a mathematical algorithm for finding the total area under glucose tolerance and other metabolic curves that has been dismissed as merely a rediscovery or simply plagiarism of the trapezoidal rule, and has been widely ridiculed....
  
  (a rediscovery of the trapezoidal rule)

External links

• Trapezoidal Rule for Numerical Integration
• Notes on the convergence of trapezoidal-rule quadrature
• Trapezoidal Rule of Integration – Notes, PPT, Videos, Mathcad, Matlab, Mathematica, Maple, Multiple Choice Tests at Holistic Numerical Methods Institute
• C Language Implementation of Trapezoidal Rule

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.