Mapping cylinder
Encyclopedia
In mathematics
, specifically algebraic topology
, the mapping cylinder of a function
between topological space
s
and 
is the quotient
where the union is disjoint, and ∼ is the equivalence relation
That is, the mapping cylinder
is obtained by gluing one end of 
× 
to 
via the map 
. Notice that the "top" of the cylinder 
is homeomorphic to 
, while the "bottom" is the space 
.
See for more details.
of
.
The projection
splits (via 
), and a deformation retraction 
is given by:
(where points in
stay fixed, which is well-defined, because 
for all 
).
, in the following sense:
Given a map
, the mapping cylinder is a space 
, together with a cofibration 
and a surjective homotopy equivalence 
(indeed, Y is a deformation retract
of
), such that the composition 
equals f.
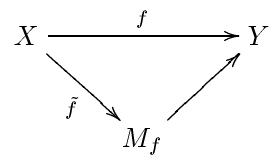
Thus the space Y gets replaced with a homotopy equivalent space
, and the map f with a lifted map 
. Equivalently, the diagram
gets replaced with a diagram
together with a homotopy equivalence between them.
The construction serves to replace any map of topological spaces by a homotopy equivalent cofibration.
Note that pointwise, a cofibration
is a closed inclusion
.
Consequently, theorems or techniques (such as homology
, cohomology
or homotopy theory) which are only dependent on the homotopy class of spaces and maps involved may be applied to
with the assumption that 
and that 
is actually the inclusion of a subspace.
Another, more intuitive appeal of the construction is that it accords with the usual mental image of a function as "sending" points of
to points of 
and hence of embedding 
within 
despite the fact that the function need not be one-to-one.
Conversely, the mapping cylinder is the homotopy pushout of the diagram where
and 
.
the mapping telescope is the homotopical direct limit
. If the maps are all already cofibrations (such as for the orthogonal groups
), then the direct limit is the union, but in general one must use the mapping telescope. The mapping telescope is a sequence of mapping cylinders, joined end-to-end. The picture of the construction looks like a stack of increasingly large cylinders, like a telescope.
Formally, one defines it as
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the mapping cylinder of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
between topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s
and is the quotientQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
where the union is disjoint, and ∼ is the equivalence relation
That is, the mapping cylinder
is obtained by gluing one end of × to via the map . Notice that the "top" of the cylinder is homeomorphic to , while the "bottom" is the space .See for more details.
Basic properties
The bottom Y is a deformation retractDeformation retract
In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
of
.The projection
splits (via ), and a deformation retraction is given by:(where points in
stay fixed, which is well-defined, because for all ).Interpretation
The mapping cylinder may be viewed as a way to replace an arbitrary map by an equivalent cofibrationCofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
, in the following sense:
Given a map
, the mapping cylinder is a space , together with a cofibration and a surjective homotopy equivalence (indeed, Y is a deformation retractDeformation retract
In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
of
), such that the composition equals f.Thus the space Y gets replaced with a homotopy equivalent space
, and the map f with a lifted map . Equivalently, the diagramgets replaced with a diagram
together with a homotopy equivalence between them.
The construction serves to replace any map of topological spaces by a homotopy equivalent cofibration.
Note that pointwise, a cofibration
Cofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
is a closed inclusion
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
.
Applications
Mapping cylinders are quite common homotopical tools. One use of mapping cylinders is to apply theorems concerning inclusions of spaces to general maps, which might not be injective.Consequently, theorems or techniques (such as homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
, cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
or homotopy theory) which are only dependent on the homotopy class of spaces and maps involved may be applied to
with the assumption that and that is actually the inclusion of a subspace.Another, more intuitive appeal of the construction is that it accords with the usual mental image of a function as "sending" points of
to points of and hence of embedding within despite the fact that the function need not be one-to-one.Categorical application and interpretation
One can use the mapping cylinder to construct homotopy limits: given a diagram, replace the maps by cofibrations (using the mapping cylinder) and then take the ordinary pointwise limit (one must take a bit more care, but mapping cylinders are a component).Conversely, the mapping cylinder is the homotopy pushout of the diagram where
and .Mapping telescope
Given a sequence of mapsthe mapping telescope is the homotopical direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
. If the maps are all already cofibrations (such as for the orthogonal groups
), then the direct limit is the union, but in general one must use the mapping telescope. The mapping telescope is a sequence of mapping cylinders, joined end-to-end. The picture of the construction looks like a stack of increasingly large cylinders, like a telescope.Formally, one defines it as