Example of a commutative non-associative magma
Encyclopedia
In mathematics
, it can be shown that there exist magmas
that are commutative but not associative. A simple example of such a magma is given by considering the children's game of rock, paper, scissors
.
and consider the binary operation
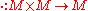defined, loosely inspired by the rock-paper-scissors
game, as follows:
"paper beats rock";
"scissors beat paper";
"rock beats scissors";
"rock ties with rock";
"paper ties with paper";
"scissors tie with scissors".
By definition, the magma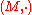
is commutative, but it is also non-associative, as the following shows:
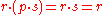
but
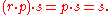
: take 
to be the three-dimensional vector space
over
whose elements are written in the form
,
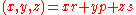for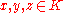
. Vector addition and scalar multiplication are defined component-wise, and vectors are multiplied using the above rules for multiplying the elements 
and 
. The set
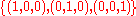i.e. 
forms a basis
for the algebra
. As before, vector multiplication in 
is commutative, but not associative.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, it can be shown that there exist magmas
Magma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
that are commutative but not associative. A simple example of such a magma is given by considering the children's game of rock, paper, scissors
Rock, Paper, Scissors
Rock-paper-scissors is a hand game played by two people. The game is also known as roshambo, or another ordering of the three items ....
.
A commutative non-associative magma
Let and consider the binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
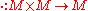defined, loosely inspired by the rock-paper-scissorsRock-paper-scissors
Rock-paper-scissors is a hand game played by two people. The game is also known as roshambo, or another ordering of the three items ....
game, as follows:
"paper beats rock"; "scissors beat paper"; "rock beats scissors"; "rock ties with rock"; "paper ties with paper"; "scissors tie with scissors".By definition, the magma
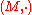is commutative, but it is also non-associative, as the following shows: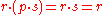but
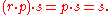
A commutative non-associative algebra
Using the above example, one can construct a commutative non-associative algebra over a fieldAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
: take to be the three-dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over
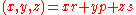whose elements are written in the form,for
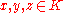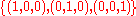. Vector addition and scalar multiplication are defined component-wise, and vectors are multiplied using the above rules for multiplying the elements and . The set i.e. forms a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the algebra
. As before, vector multiplication in is commutative, but not associative.